本节内容其实是接在特征向量与特征值里实对称矩阵的对角化来说的。即他的上一节应该是 实对称矩阵的对角化
但是,因为向量太重要了,我们有必要花费大的篇幅来介绍向量的性质,因此本篇增加了很多向量知识,很多教程在介绍向量知识都是一笔带过的。
我们在 实对称矩阵的对角化 里介绍了 ①对称矩阵A的好处,介绍了②对角化Λ 的好处,但是,如何把实对称矩阵对角化?这就是 上一节介绍的 ③正交矩阵Q。
现在①②③都学完了,问题就来了:给你一个矩阵A如何找Q来相似Λ 这就是本节的内容。求正交矩阵Q是本章考察的重点。
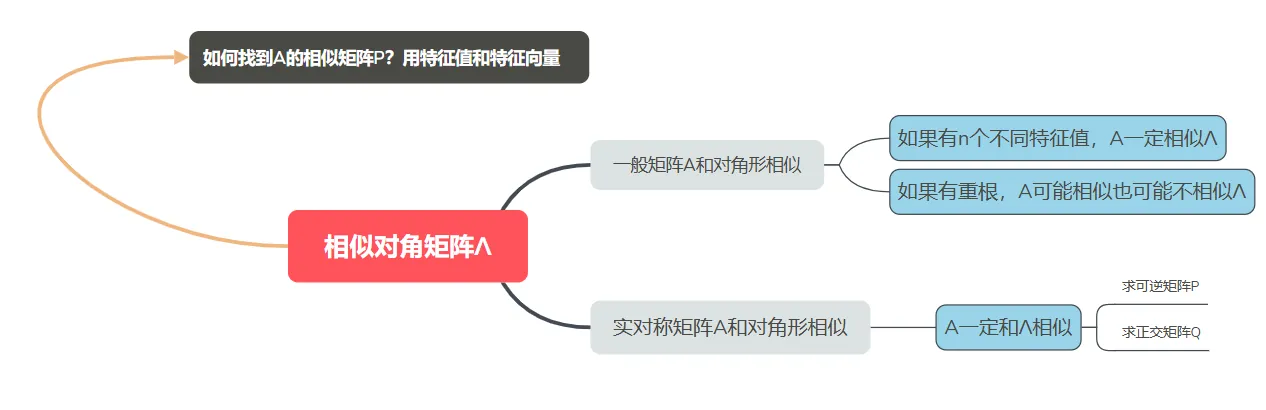
用正交阵将实对称矩阵 A 化为对角阵的步骤:
(i)求出 A 的所有相异的特征值 λ1,λ2,⋯⋯,λm ;
(ii)对每一个重特征值 λi ,求出对应的 ri 个线性无关的特征向量 ξi1,ξi2,⋯,ξiri;(i=1,2,⋯,m) ,由性质知 ∑i=1mri=n .
(iii)用施密特正交化方法将每一个重特征值 λi 所对应的 ri 个线性无关的特征向量 ξi1,ξi2,⋯,ξiri(i=1,2,⋯,m) 先正交化再单位化为 ηi1,ηi2,⋯,ηiii(i=1,2,⋯,m) ;它们仍为属于 λi 的特征向量。
(iv)将上面求得的正交单位向量,排成一个 n 阶方阵 Q ,则 Q即为所求的正交方阵。此时 Q−1AQ=QTAQ=Λ 为对角阵。
例题
例设矩阵 A=1030−10202, 求正交阵 P ,使得 P−1A=PTAP 为对角阵。
解 由
∣A−λE∣=1−λ030−1−λ0202−λ=−(λ−4)(λ+1)2=0 得特征值为 λ1=4,λ2=λ3=−1.
对特征值 λ1=4 ,解齐次线性方程组 (A−4E)x=0 ,由
A−4E=−3030−5020−2100010−3200, 取特征向量为 α1=203 ,单位化,得 η1=∣αa∣α11=1320133.
对特征值 λ2=λ3=−1 ,解齐次线性方程组 (A+E)x=0 ,由
A+E=203000203+100000100, 取特征向量为 α2=010,α3=−101.由于 α2 与 α3 已经正交,所以只需将这两个向量单位化,得
η2=α2=010,η3=∥α3∥1α3=−22022. 令矩阵 P=(η1,η2,η3)=1320133010−22022 ,则 P−1AP=PTAP=4−1−1.
例 设 A=211121112 ,求 A10 。
解:因为 A 是实对称阵,从而可求一个正交阵 P ,使得 P−1AP=Λ=λ1λ2λ3, 其中 λ1,λ2,λ3
是 A 的全部特征值.于是
A10=(PΛP−1)10=PΛ10P−1=PΛ10PT. 由
∣A−λE∣=2−λ1112−λ1112−λ=−(λ−4)(λ−1)2=0 得特征值为 λ1=4,λ2=λ3=1.
对特征值 λ1=4 ,解齐次线性方程组 (A−4E)x=0 ,由
A−4E=−2111−2111−2100010−1−10, 取特征向量为 α1=111 ,单位化,得 p1=∣α1∣α11=333333.
对特征值 λ2=λ3=1 ,解齐次线性方程组 (A−E)x=0 ,由
A−E=111111111∼∼100100100, 取特征向量为 α2=−110,α3=−101.
先将 α2 与 α3 正交化:令
β2=α2=−110,β3=α3−(β2,β2)(α3,β2)β2=−101−21−110=21−1−12, 再将 β2,β3 单位化,得
p2=∥β2∥1β2=−22220,p3=∥β3∥1β3=−66−6636。 令矩阵 P=(p1,p2,p3)=333333−22220−66−6636 ,则 P 为所求正交阵,且 Λ=411 ,
从而
A10=P41110PT=P41011PT=31410+2410−1410−1410−1410+2410−1410−1410−1410+2. 