1.2_基于RNN的语言模型

1.2 基于 RNN 的语言模型

循环神经网络（Recurrent Neural Network, RNN）是一类网络连接中包含环路的神经网络的总称。给定一个序列，RNN 的环路用于将历史状态叠加到当前状态上。沿着时间维度，历史状态被循环累积，并作为预测未来状态的依据。因此，RNN 可以基于历史规律，对未来进行预测。基于 RNN 的语言模型，以词序列作为输入，基于被循环编码的上文和当前词来预测下一个词出现的概率。本节将先对原始 RNN 的基本原理进行介绍，然后讲解如何利用 RNN 构建语言模型。

1.2.1 循环神经网络 RNN

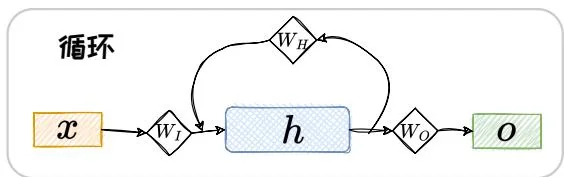
按照推理过程中信号流转的方向，神经网络的正向传播范式可分为两大类：前馈传播范式和循环传播范式。在前馈传播范式中，计算逐层向前，“不走回头路”。而在循环传播范式中，某些层的计算结果会通过环路被反向引回前面的层中，形成“螺旋式前进”的范式。采用前馈传播范式的神经网络可以统称为前馈神经网络（Feed-forward Neural Network, FNN），而采用循环传播范式的神经网络被统称为循环神经网络（Recurrent Neural Network, RNN）。以包含输入层、隐藏层、输出层的神经网络为例。图1.2中展示了最简单的FNN和RNN的网络结构示意图，可见FNN网络结构中仅包含正向通路。而RNN的网络结构中除了正向通路，还有一条环路将某层的计算结果再次反向连接回前面的层中。


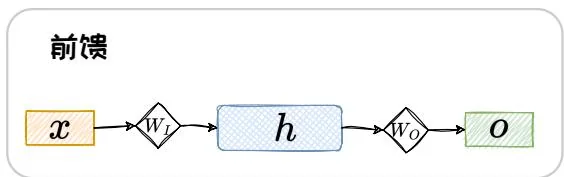
图1.2: 前馈传播范式与循环传播范式的对比。

设输入序列为 {x1,x2,x3,…,xt}\{x_{1}, x_{2}, x_{3}, \ldots, x_{t}\} ，隐状态为 {h1,h2,h3,…,ht}\{h_{1}, h_{2}, h_{3}, \ldots, h_{t}\} ，对应输出为 {o1,o2,o3,…,ot}\{o_{1}, o_{2}, o_{3}, \ldots, o_{t}\} ，输入层、隐藏层、输出层对应的网络参数分别为 WI,WH,WOW_{I}, W_{H}, W_{O} 。 g(⋅)g(\cdot) 为激活函数， f(⋅)f(\cdot) 为输出函数。将输入序列一个元素接着一个元素地串行输入时，对于 FNN，当前的输出只与当前的输入有关，即

ot=f(WOg(WIxt))。(1.18)o _ {t} = f \left(W _ {O} g \left(W _ {I} x _ {t}\right)\right) 。 \tag {1.18}

此处为方便对比，省去了偏置项。独特的环路结构导致 RNN 与 FNN 的推理过程完全不同。RNN 在串行输入的过程中，前面的元素会被循环编码成隐状态，并叠加到当前的输入上面。其在 tt 时刻的输出如下：

ht=g(WHht−1+WIxt)=g(WHg(WHht−2+WIxt−1)+WIxt)=……(1.19)h _ {t} = g \left(W _ {H} h _ {t - 1} + W _ {I} x _ {t}\right) = g \left(W _ {H} g \left(W _ {H} h _ {t - 2} + W _ {I} x _ {t - 1}\right) + W _ {I} x _ {t}\right) = \dots \dots \tag {1.19}
ot=f(WOht)∘o _ {t} = f (W _ {O} h _ {t}) _ {\circ}

其中, t>0,h0=0t > 0, h_0 = 0 。将此过程按照时间维度展开, 可得到 RNN 的推理过程, 如图1.3所示。注意, 图中展示的 tt 时刻以前的神经元, 都是过往状态留下的 “虚影” 并不真实存在, 如此展开只是为了解释 RNN 的工作方式。

可以发现，在这样一个元素一个元素依次串行输入的设定下，RNN 可以将历史状态以隐变量的形式循环叠加到当前状态上，对历史信息进行考虑，呈现出螺旋式前进的模式。但是，缺乏环路的 FNN 仅对当前状态进行考虑，无法兼顾历史状态。以词序列 {长颈鹿, 脖子, 长} 为例，在给定“脖子”来预测下一个词是什么的时候，FFN 将仅仅考虑“脖子”来进行预测，可能预测出的下一词包含“短”，“疼”等等；而 RNN 将同时考虑“长颈鹿”和“脖子”，其预测出下一词是“长”的概率将更高，历史信息“长颈鹿”的引入，可以有效提升预测性能。


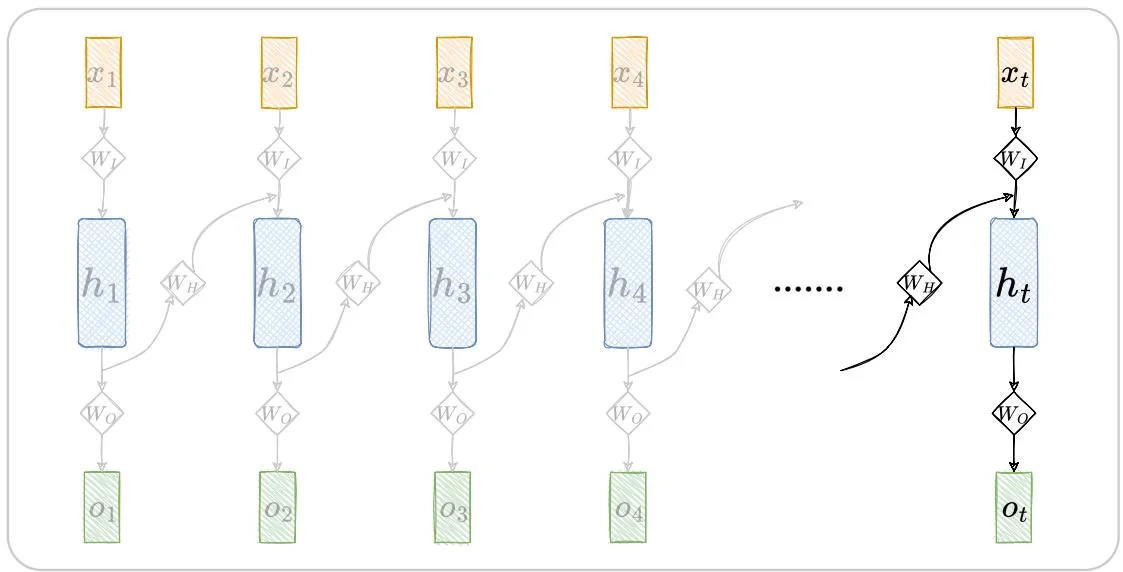
图1.3: RNN推理过程从时间维度拆解示意图。

如果 FNN 想要做到对历史信息进行考虑，则需要将所有元素同时输入到模型中去，这将导致模型参数量的激增。虽然，RNN 的结构可以让其在参数量不扩张的情况下实现对历史信息的考虑，但是这样的环路结构给 RNN 的训练带来了挑战。在训练 RNN 时，涉及大量的矩阵联乘操作，容易引发梯度衰减或梯度爆炸问题。具体分析如下：

设 RNN 语言模型的训练损失为:

L=L(x,o,WI,WH,WO)=∑i=1tl(oi,yi)。(1.20)L = L (x, o, W _ {I}, W _ {H}, W _ {O}) = \sum_ {i = 1} ^ {t} l \left(o _ {i}, y _ {i}\right) 。 \tag {1.20}

其中， l(⋅)l(\cdot) 为损失函数， yiy_{i} 为标签。

损失 LL 关于参数 WHW_{H} 的梯度为:

∂LWH=∑i=1t∂lt∂ot⋅∂ot∂ht⋅∂ht∂hi⋅∂hi∂WH。(1.21)\frac {\partial L}{W _ {H}} = \sum_ {i = 1} ^ {t} \frac {\partial l _ {t}}{\partial o _ {t}} \cdot \frac {\partial o _ {t}}{\partial h _ {t}} \cdot \frac {\partial h _ {t}}{\partial h _ {i}} \cdot \frac {\partial h _ {i}}{\partial W _ {H}} 。 \tag {1.21}

其中，

∂ht∂hi=∂ht∂ht−1∂ht−1∂ht−2…∂hi+1∂hi=∏k=i+1t∂hk∂hk−1。(1.22)\frac {\partial h _ {t}}{\partial h _ {i}} = \frac {\partial h _ {t}}{\partial h _ {t - 1}} \frac {\partial h _ {t - 1}}{\partial h _ {t - 2}} \dots \frac {\partial h _ {i + 1}}{\partial h _ {i}} = \prod_ {k = i + 1} ^ {t} \frac {\partial h _ {k}}{\partial h _ {k - 1}} 。 \tag {1.22}

并且，

∂hk∂hk−1=∂g(zk)∂zkWH。(1.23)\frac {\partial h _ {k}}{\partial h _ {k - 1}} = \frac {\partial g (z _ {k})}{\partial z _ {k}} W _ {H} 。 \tag {1.23}

其中， zk=WHhk−1+WIxkz_{k} = W_{H}h_{k - 1} + W_{I}x_{k} 。综上，有

∂LWH=∑i=1t∂lt∂ot⋅∂ot∂ht⋅∏k=it∂g(zk)∂zkWH⋅∂hi∂WH。(1.24)\frac {\partial L}{W _ {H}} = \sum_ {i = 1} ^ {t} \frac {\partial l _ {t}}{\partial o _ {t}} \cdot \frac {\partial o _ {t}}{\partial h _ {t}} \cdot \prod_ {k = i} ^ {t} \frac {\partial g \left(z _ {k}\right)}{\partial z _ {k}} W _ {H} \cdot \frac {\partial h _ {i}}{\partial W _ {H}} 。 \tag {1.24}

从上式中可以看出，求解 WHW_{H} 的梯度时涉及大量的矩阵级联相乘。这会导致其数值被级联放大或缩小。文献[17]中指出，当 WHW_{H} 的最大特征值小于1时，会发生梯度消失；当 WHW_{H} 的最大特征值大于1时，会发生梯度爆炸。梯度消失和爆炸导致训练上述RNN非常困难。为了解决梯度消失和爆炸问题，GRU[4]和LSTM[8]引入门控结构，取得了良好效果，成为主流的RNN网络架构。

1.2.2 基于 RNN 的语言模型

对词序列 {w1,w2,w3,…,wN}\{w_{1}, w_{2}, w_{3}, \dots, w_{N}\} ，基于 RNN 的语言模型每次根据当前词 wiw_{i} 和循环输入的隐藏状态 hi−1h_{i-1} ，来预测下一个词 wi+1w_{i+1} 出现的概率，即

P(wi+1∣w1:i)=P(wi+1∣wi,hi−1)。(1.25)P \left(w _ {i + 1} \mid w _ {1: i}\right) = P \left(w _ {i + 1} \mid w _ {i}, h _ {i - 1}\right) 。 \tag {1.25}

其中，当 i=1i = 1 时， P(wi+1∣wi,hi−1)=P(w2∣w1)P(w_{i + 1}|w_i,h_{i - 1}) = P(w_2|w_1) 。基于此， {w1,w2,w3,…,wN}\{w_1,w_2,w_3,\ldots ,w_N\} 整体出现的概率为：

P(w1:N)=∏i=1N−1P(wi+1∣wi,hi−1)。(1.26)P \left(w _ {1: N}\right) = \prod_ {i = 1} ^ {N - 1} P \left(w _ {i + 1} \mid w _ {i}, h _ {i - 1}\right) 。 \tag {1.26}

在基于 RNN 的语言模型中，输出为一个向量，其中每一维代表着词典中对应词的概率。设词典 DD 中共有 ∣D∣|D| 个词 {w^1,w^2,w^3,…,w^∣D∣}\{ \hat{w}_1, \hat{w}_2, \hat{w}_3, \dots, \hat{w}_{|D|} \} ，基于 RNN 的语言模型的输出可表示为 oi={oi[w^d]}d=1∣D∣o_i = \{ o_i[\hat{w}_d] \}_{d=1}^{|D|} ，其中， oi[w^d]o_i[\hat{w}_d] 表示词典中的词 w^d\hat{w}_d 出现的概率。因此，对基于 RNN 的语言模型有

P(w1:N)=∏i=1N−1P(wi+1∣w1:i)=∏i=1Noi[wi+1]。(1.27)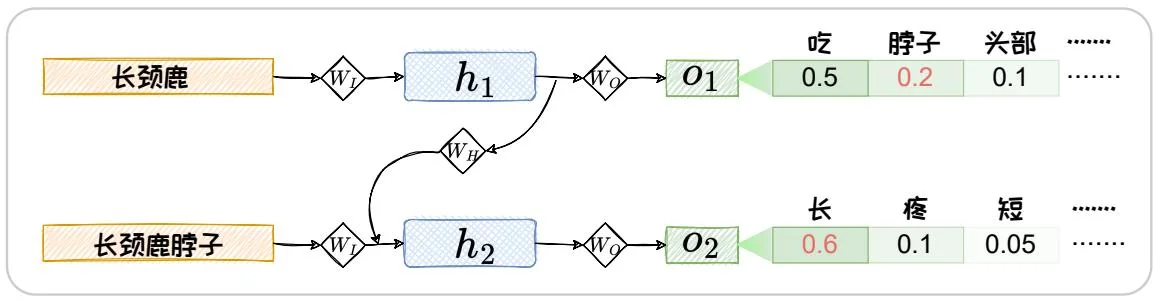P \left(w _ {1: N}\right) = \prod_ {i = 1} ^ {N - 1} P \left(w _ {i + 1} \mid w _ {1: i}\right) = \prod_ {i = 1} ^ {N} o _ {i} \left[ w _ {i + 1} \right] 。 \tag {1.27}


图1.4：RNN计算词序列概率示意图。

以下举例对上述过程进行说明。假设词表 D={脖子,头部,吃,长,疼,吃,短}D = \{\text{脖子}, \text{头部}, \text{吃}, \text{长}, \text{疼}, \text{吃}, \text{短}\} ,基于 RNN 的语言模型计算 “长颈鹿脖子长” 的概率的过程如图 1.4 所示。

P(长 颈 鹿 脖 子 长)=P(脖 子∣长 颈 鹿)⋅P(长∣脖 子,h1)=0.2×0.6=0.12。(1.28)P (\text {长 颈 鹿 脖 子 长}) = P (\text {脖 子} | \text {长 颈 鹿}) \cdot P (\text {长} | \text {脖 子}, h _ {1}) = 0. 2 \times 0. 6 = 0. 1 2 。 \tag {1.28}

基于以上预训练任务，对RNN语言模型进行训练时，可选用如下交叉熵函数作为损失函数。

lCE(oi)=−∑d=1∣D∣I(w^d=wi+1)log⁡oi[wi+1]=−log⁡oi[wi+1],(1.29)l _ {C E} \left(o _ {i}\right) = - \sum_ {d = 1} ^ {| D |} I \left(\hat {w} _ {d} = w _ {i + 1}\right) \log o _ {i} \left[ w _ {i + 1} \right] = - \log o _ {i} \left[ w _ {i + 1} \right], \tag {1.29}

其中， I(⋅)I(\cdot) 为指示函数，当 w^d=wi+1\hat{w}_d = w_{i+1} 时等于1，当 w^d≠wi+1\hat{w}_d \neq w_{i+1} 时等于0。

设训练集为 S，RNN 语言模型的损失可以构造为：

L(S,WI,WH,WO)=1N∣S∣∑s=1∣S∣∑i=1NlCE(oi,s),(1.30)L \left(S, W _ {I}, W _ {H}, W _ {O}\right) = \frac {1}{N | S |} \sum_ {s = 1} ^ {| S |} \sum_ {i = 1} ^ {N} l _ {C E} \left(o _ {i, s}\right), \tag {1.30}

其中， oi,so_{i,s} 为 RNN 语言模型输入第 ss 个样本的第 ii 个词时的输出。此处为方便表述，假设每个样本的长度都为 NN 。在此损失的基础上，构建计算图，进行反向传播，便可对 RNN 语言模型进行训练。上述训练过程结束之后，我们可以直接利用此模型对序列数据进行特征抽取。抽取的特征可以用于解决下游任务。此外，我们还可以对此语言模型的输出进行解码，在“自回归”的范式下完成文本生成任务。在自回归中，第一轮，我们首先将第一个词输入给 RNN 语言模型，经过解码，得到一个输出词。然后，我们将第一轮输出的词与第一轮输入的词拼接，作为第二轮

的输入，然后解码得到第二轮的输出。接着，将第二轮的输出和输入拼接，作为第三轮的输入，以此类推。每次将本轮预测到的词拼接到本轮的输入上，输入给语言模型，完成下一轮预测。在循环迭代的“自回归”过程中，我们不断生成新的词，这些词便构成了一段文本。

但上述“自回归”过程存在着两个问题：(1) 错误级联放大，选用模型自己生成的词作为输入可能会有错误，这样的错误循环输入，将会不断的放大错误，导致模型不能很好拟合训练集；（2）串行计算效率低，因为下一个要预测的词依赖上一次的预测，每次预测之间是串行的，难以进行并行加速。为了解决上述两个问题，“Teacher Forcing”[21]在语言模型预训练过程中被广泛应用。在Teacher Forcing中，每轮都仅将输出结果与“标准答案”（Ground Truth）进行拼接作为下一轮的输入。在图1.4所示的例子中，第二轮循环中，我们用“长颈鹿脖子”来预测下一个词“长”，而非选用 o1o_1 中概率最高的词“吃”或者其他可能输出的词。

但是，Teacher Forcing的训练方式将导致曝光偏差（Exposure Bias）的问题。曝光偏差是指Teacher Forcing训练模型的过程和模型在推理过程存在差异。Teacher Forcing在训练中，模型将依赖于“标准答案”进行下一次的预测，但是在推理预测中，模型“自回归”的产生文本，没有“标准答案”可参考。所以模型在训练过程中和推理过程中存在偏差，可能推理效果较差。为解决曝光偏差的问题，Bengio等人提出了针对RNN提出了Scheduled Sampling方法[2]。其在Teacher Forcing的训练过程中循序渐进的使用一小部分模型自己生成的词代替“标准答案”，在训练过程中对推理中无“标准答案”的情况进行预演。

由于 RNN 模型循环迭代的本质，其不易进行并行计算，导致其在输入序列较长时，训练较慢。下节将对容易并行的基于 Transformer 的语言模型进行介绍。

上一章1.1_基于统计方法的语言模型
下一章1.3_基于Transformer的语言模型