13.3 扫描和电路设计

经过分析扫描的一种并行算法，现在就变得明朗了，我们可以找到许多不同的方法来实现并行扫描算法。为指导其他可能的实现，我们可以借助执行类似功能的整型加法硬件的设计方法：不是传递一个任意的二元可结合操作符 $\oplus$ 给数组，然后使用归约获得最终输出，而是硬件加法器传播部分加法结果，连带进位，可以传播给多倍精度运算。

硬件设计师使用有向无环、定向图来表示扫描“电路”的不同实现。这些示意图简洁地表达出数据流和并行性。代码清单13-1这一串行实现的示意图在图13-6中给出。随时间推移，不断向下推进；垂直线表示导线，信号通过它进行传播。在入度为2的节点（“操作节点”）上，对它们的输入应用操作符 $\oplus$ 。

注意，该电路图展示的是包容性扫描，而不是排他性扫描。对于电路图而言，包容性扫描与排他性扫描之间的区别甚微。欲把图13-6中的包容性扫描转换成一个排他性扫描，把一个0连接到第一个输出，并把随后求得的和依次连接到输出，如图13-7所示。注意到不论是包容性还是排他性扫描都是把针对输入数组生成的归约作为输出，这一特性将用于构建高效的扫描算法。（为清楚起见，除了图13-7之外的所有电路图仅绘制包容性扫描。）

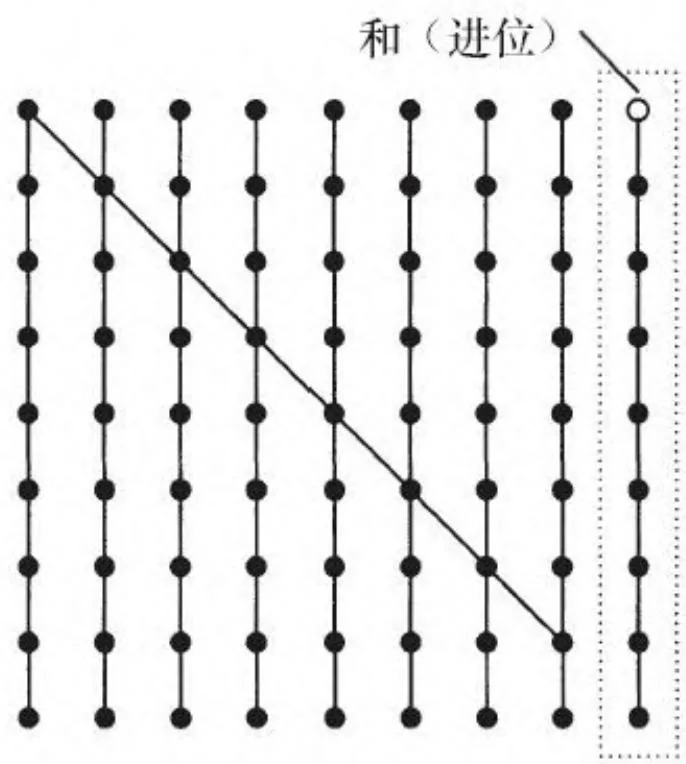
图13-6 串行扫描

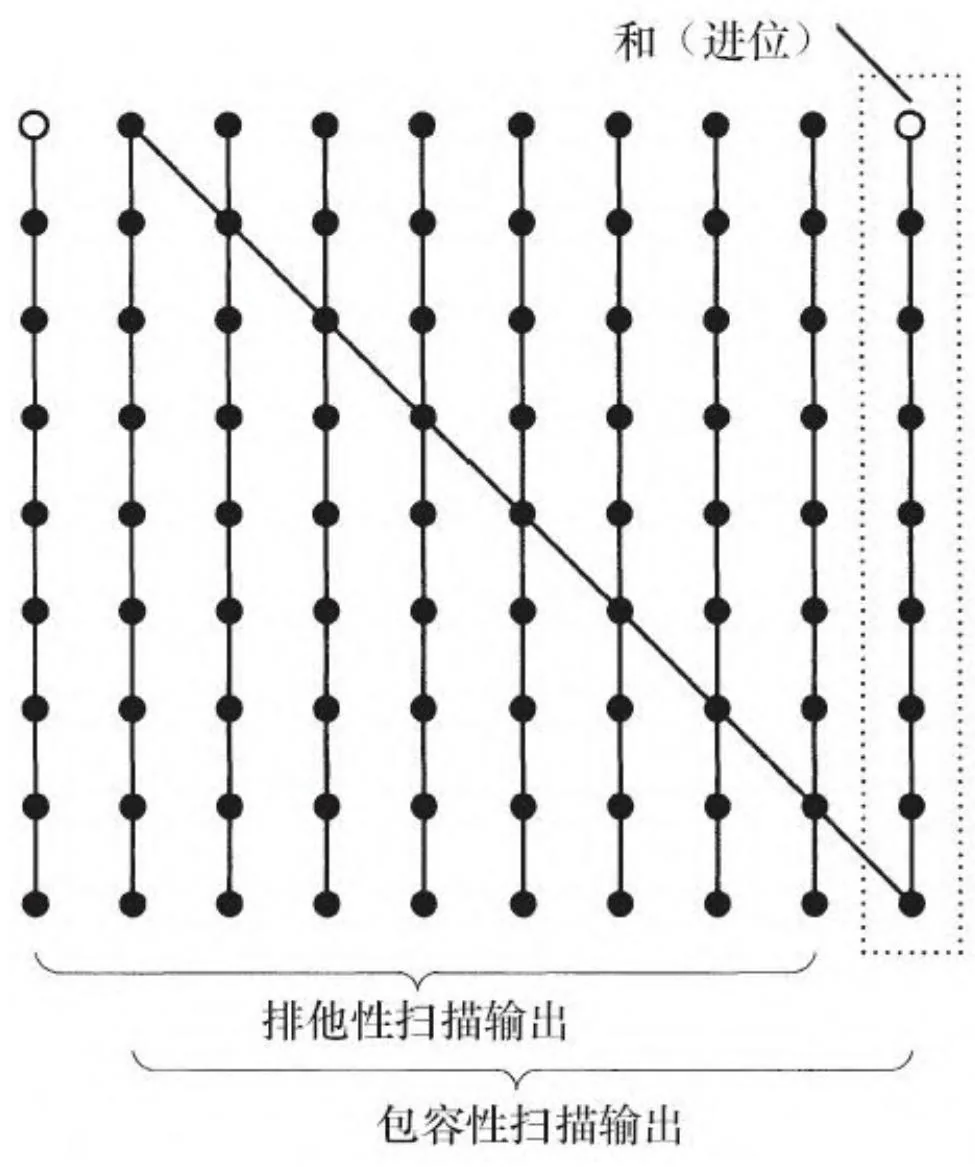
图13-7 串行扫描（包容性和排他性）

Blelloch描述的扫描算法对应于Brent-Kung电路设计法，采用一个递归分解，其中每隔一个输出被送入只有当前一半宽度的Brent-Kung电路。图13-8展示了长度为8的Brent-Kung电路的例子，同时伴随有Blelloch的自底向上阶段和自顶向下阶段。请注意，下一步中把输

出广播到多个节点的行为称为扇出（fan out）。Brent-Kung电路的值得注意的特点是具有恒定的2个扇出分支。

Brent-Kung电路的结构对大型电路变得更清晰。请考察如图13-9所示包含16个输入的电路。图13-9也加粗了电路的“脊椎”，该脊椎是用于生成扫描输出最后一个元素的最长子图。

Brent-Kung电路的深度随输入的数量呈对数增长，展示了比串行算法更强的效率。但是由于递归分解的每一步电路深度会增加2，Brent-Kung电路的深度不是最小深度。Sklansky描述了一个构建最小深度电路的方法，像图13-10那样递归的分解它们。

2个输入为N/2的电路被并行运行，并且左侧电路的脊柱的输出被添加到右侧电路中的每个元素。对于我们16个元素的例子，该递归的左侧子图在图13-10中被特别框出。

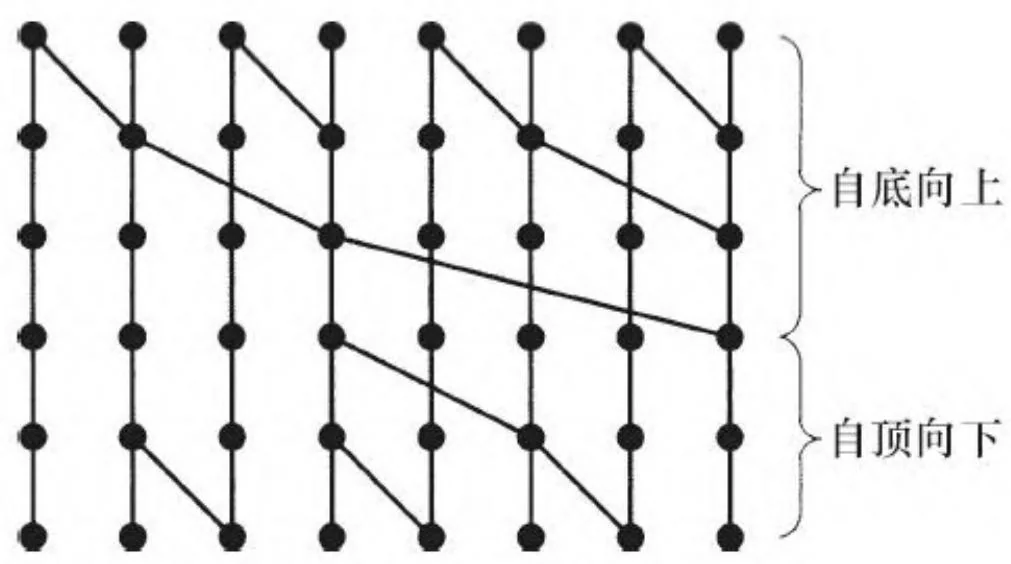
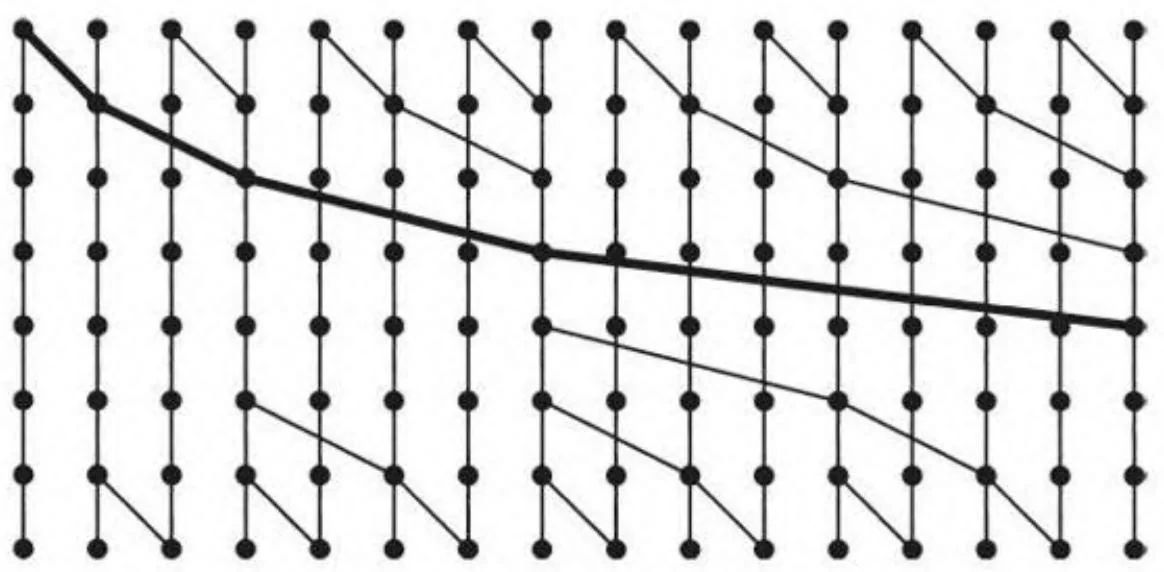
图13-8 Brent-Kung电路

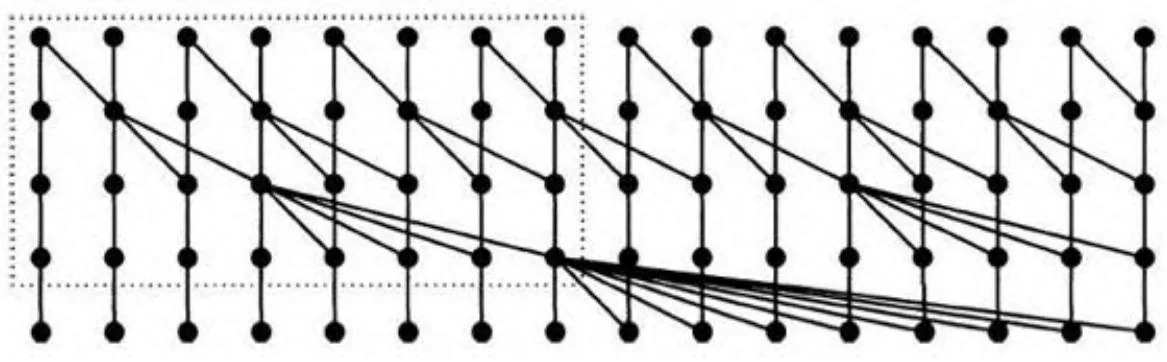
图13-9 Brent-Kung电路（16个输入数据）
图13-10 Sklansky（最小深度）电路

另一种最小深度的扫描电路，称为Kogge-Stone电路。它具有恒定的2个扇出分支，这是硬件实现最期望的特性。但是，正如你在图13-11所见，它有许多操作节点，模拟Kogge-Stone电路的软件实现效率低下。

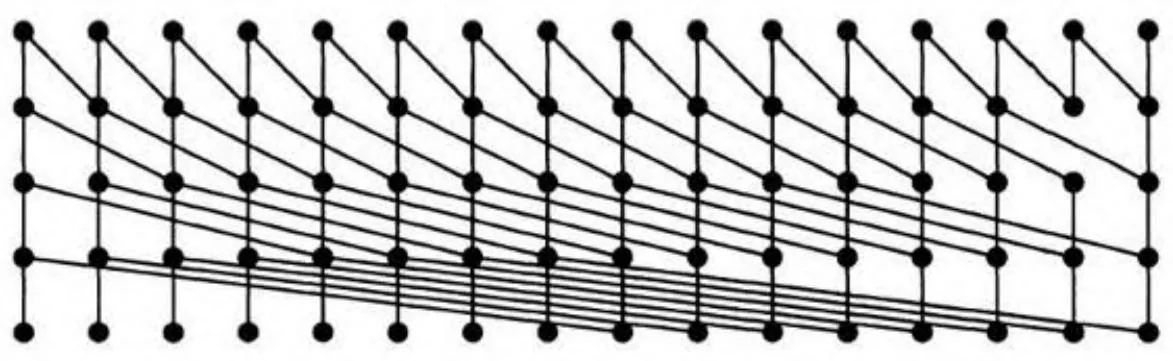
图13-11 Kogge-Stone电路

任何扫描电路都可以通过组合扫描（执行并行的前缀求和计算并生成输入数组的和作为输出）和扇出（把一个输入添加到剩余的每个输出）来构成。如图13-10所示具有最小深度的电路在它们的递归定义中大量使用了扇出操作。

要得到一个优化的CUDA实现，一个重要指导思想是，扇出操作不需要从扫描本身得到它的输入，任何归约都能做到。而在第12章，我们已经拥有了一个高度优化的归约算法。

例如，如果我们把输入数组分割成长度为b的子数组，并使用我们优化了的归约程序计算每个子数组的总和，我们最终得到一个由 $\lceil N / b\rceil$ 个归约值构成的数组。如果我们在该数组上执行排他性扫描，得到的数组变成了扇出操作的输入（种子），用于对应子数组的扫描。通过在全局内存的一遍扫描可以有效扫描到的值受制于CUDA的线程块大小和共享内存大小，因此对于较大的输入，这种方法必须递归的应用。