12.1 Overview

Since the binary operator is associative, the $O(N)$ operations to compute a reduction may be performed in any order.

Figure 12.1 shows some different options to process an 8-element array. The serial implementation is shown for contrast. Only one execution unit that can

Serial $(\mathsf{a}_0\oplus (\mathsf{a}_1\oplus (\mathsf{a}_2\oplus (\mathsf{a}_3\oplus (\mathsf{a}_4\oplus (\mathsf{a}_5\oplus (\mathsf{a}_6\oplus \mathsf{a}_7)))))))$

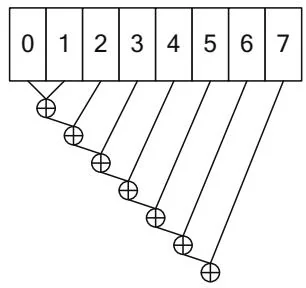
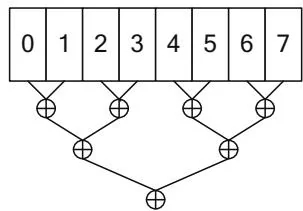
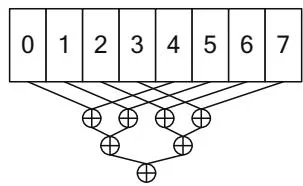
Figure 12.1. Reduction of 8 elements.

Log-Step Reduction (pairwise)

$((\mathbf{a}_0 \oplus \mathbf{a}_1) \oplus (\mathbf{a}_2 \oplus \mathbf{a}_3)) \oplus ((\mathbf{a}_4 \oplus \mathbf{a}_5) \oplus (\mathbf{a}_6 \oplus \mathbf{a}_7))))$

Log-Step Reduction (interleaved)

$((\mathbf{a}_0\oplus \mathbf{a}_1)\oplus (\mathbf{a}_2\oplus \mathbf{a}_3))\oplus ((\mathbf{a}_4\oplus \mathbf{a}_5)\oplus (\mathbf{a}_6\oplus \mathbf{a}_7))))$

perform the $\oplus$ operator is needed, but performance is poor because it takes 7 steps to complete the computation.

The pairwise formulation is intuitive and only requires $O(\lg N)$ steps (3 in this case) to compute the result, but it exhibits poor performance in CUDA. When reading global memory, having a single thread access adjacent memory locations causes uncoalesced memory transactions. When reading shared memory, the pattern shown will cause bank conflicts.

For both global memory and shared memory, an interleaving-based strategy works better. In Figure 12.1, the interleaving factor is 4; for global memory, interleaving by a multiple of $\text{blockDim.x} * \text{gridDim.x}$ has good performance because all memory transactions are coalesced. For shared memory, best performance is achieved by accumulating the partial sums with an interleaving factor chosen to avoid bank conflicts and to keep adjacent threads in the thread block active.

Once a thread block has finished processing its interleaved subarray, it writes the result to global memory for further processing by a subsequent kernel launch. It may seem expensive to launch multiple kernels, but kernel launches are asynchronous, so the CPU can request the next kernel launch while the GPU is executing the first; every kernel launch represents an opportunity to specify different launch configurations.

Since the performance of a kernel can vary with different thread and block sizes, it's a good idea to write the kernel so it will work correctly for any valid combination of thread and block sizes. The optimal thread/block configuration then can be determined empirically.

The initial reduction kernels in this chapter illustrate some important CUDA programming concepts that may be familiar.

• Coalesced memory operations to maximize bandwidth

• Variable-sized shared memory to facilitate collaboration between threads

• Avoiding shared memory bank conflicts

The optimized reduction kernels illustrate more advanced CUDA programming idioms.

• Warp synchronous coding avoids unneeded thread synchronization.

• Atomic operations and memory fences eliminate the need to invoke multiple kernels.

• The shuffle instruction enables warp-level reductions without the use of shared memory.