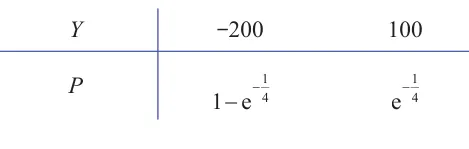2._数学期望的定义

随机变量的分布函数、分布律或概率密度虽然能完整地描述随机变量的统计规律，但在实际问题中，随机变量的分布往往不容易确定，而且有些问题并不需要知道随机变量分布规律的全貌，只需要知道它的某些特征就够了。例如，考察 LED灯管的质量时，常常关注的是 LED 灯管的平均寿命，这说明随机变量的平均值是一个重要的数量特征(称作期望）。又例如，比较两台机床生产精度的高低，不仅要看它们生产的零件的平均尺寸，还必须考察每个零件尺寸与平均尺寸的偏离程度，只有偏离程度较小的才是精度高的（称作方差），这说明随机变量与其平均值偏离的程度也是一个重要的数量特征。

数学期望反映了在大量重复试验中，某个随机事件的“平均结果”。例如 掷骰子 每个点数（1-6）出现的概率均为1/6，期望值为 (1+2+3+4+5+6)/6 = 3.5。虽然实际掷骰子不会出现3.5，但若重复无数次，平均点数会趋近于3.5。 再如 赌博场景 ：若轮盘赌押中一个数字的概率是1/38，奖金为35倍本金，期望收益为 (1/38)×35 + (37/38)×(-1) ≈ -0.0526美元，即长期每赌一次平均亏约5美分

离散型数学期望的定义

设 XX 是离散型随机变量，其分布律为

P(X=xi)=pi,i=1,2,⋯P\left(X=x_i\right)=p_i, \quad i=1,2, \cdots

当级数 ∑ixipi\sum_i x_i p_i 绝对收敛时, 称 ∑ixipi\sum_i x_i p_i 为随机变量 XX 的数学期望 (或期望、均值)，记作 E(X)E(X).

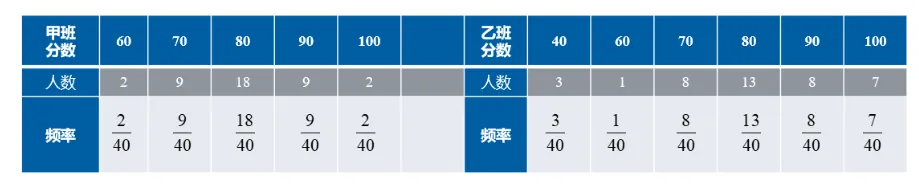
例 设甲、乙两班各 40 名学生，概率统计成绩及得分人数如表所示， 甲、乙两班概率统计的平均成绩各是多少？

图片

解：（1）甲班平均成绩 =60×240+70×940+80×1840+90×940+100×240=80=60 \times \frac{2}{40}+70 \times \frac{9}{40}+80 \times \frac{18}{40}+90 \times \frac{9}{40}+100 \times \frac{2}{40}=80（分）

（2）同理，乙班平均成绩 =80=80（分）

注意： 1）为保证无穷级数 ∑ixipi\sum_i x_i p_i 的值不因改变求和次序而变，要求级数 ∑ixipi\sum_i x_i p_i绝对收敛，E(X)E(X) 才有定义。

2） 当 XX 服从某个分布时，也称 E(X)E(X) 是 这个分布的期望。期望刻画随机变量取值的平均，有直观含义。

例设随机变量 XX 的分布律分别为 （1）P(X=2ii)=12i,i=1,2,⋯P\left(X=\frac{2^i}{i}\right)=\frac{1}{2^i}, i=1,2, \cdots （2）P(X=(−1)i2ii)=12i,i=1,2,⋯P\left(X=(-1)^i \frac{2^i}{i}\right)=\frac{1}{2^i}, i=1,2, \cdots （3）P(X=(−1)i2ii2)=12i,i=1,2,⋯P\left(X=(-1)^i \frac{2^i}{i^2}\right)=\frac{1}{2^i}, i=1,2, \cdots 在三种情形下，试问 XX 的数学期望 E(X)E(X) 是否存在吗？为什么？

解（1）因为 ∑i=1∞∣xi∣pi=∑i=1∞2ii⋅12i=∑i=1∞1i\sum_{i=1}^{\infty}\left|x_i\right| p_i=\sum_{i=1}^{\infty} \frac{2^i}{i} \cdot \frac{1}{2^i}=\sum_{i=1}^{\infty} \frac{1}{i} 发散，所以 XX 的数学期望不存在。 （2）因为 ∑i=1∞∣xi∣pi=∑i=1∞∣(−1)i2ii∣⋅12i=∑i=1∞1i\sum_{i=1}^{\infty}\left|x_i\right| p_i=\sum_{i=1}^{\infty}\left|(-1)^i \frac{2^i}{i}\right| \cdot \frac{1}{2^i}=\sum_{i=1}^{\infty} \frac{1}{i} 发散，所以 XX 的数学期望不存在。 （3）因为 ∑i=1∞∣xi∣pi=∑i=1∞2ii2⋅12i=∑i=1∞1i2\sum_{i=1}^{\infty}\left|x_i\right| p_i=\sum_{i=1}^{\infty} \frac{2^i}{i^2} \cdot \frac{1}{2^i}=\sum_{i=1}^{\infty} \frac{1}{i^2} 收敛，所以 XX 的数学期望存在。

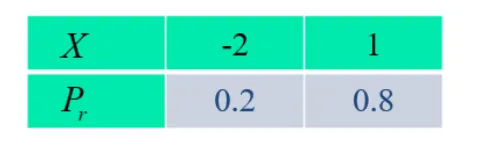
例 设离散型随机变量 XX 的分布律如下，计算 E(X)E(X) 图片

解 E(X)=∑ixipi=−2×0.2+1×0.8=0.4E(X)=\sum_i x_i p_i=-2 \times 0.2+1 \times 0.8=0.4

连续型数学期望的定义

设 XX 是连续型随机变量，其密度函数为 f(x)f(x) ，如果广义积分 ∫−∞+∞xf(x)dx\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x 绝对收玫, 则称

E(X)=∫−∞+∞xf(x)dx.E(X)=\int_{-\infty}^{+\infty} x f(x) \mathrm{d} x .

为连续型随机变量 XX 的数学期望, 也称作期望或均值。

例设有离散型随机变量 XX ，在下列三种情况下计算随机变量 XX 的数学期望 E(X)E(X) (1) X∼B(1,p)X \sim B(1, p); (2) X∼B(n,p)X \sim B(n, p); (3) X∼P(λ)X \sim P(\lambda). 解 (1) 因为 X∼B(1,p)X \sim B(1, p), 所以 E(X)=∑ixipi=0⋅q+1⋅p=pE(X)=\sum_i x_i p_i=0 \cdot q+1 \cdot p=p (2) 因为 X∼B(n,p)X \sim B(n, p), 所以 P(X=k)=(nk)pkqn−k,k=0,1,2,⋯ ,nP(X=k)=\left(\begin{array}{l}n \\ k\end{array}\right) p^k q^{n-k}, k=0,1,2, \cdots, n. 由期望的定义得

E(X)=∑k=0nkn!k!(n−k)!pkqn−k=∑k=1nn!(k−1)!(n−k)!pkqn−k=np∑k=1n(n−1)!(k−1)!(n−k)!pk−1qn−1−(k−1)\begin{aligned} & E(X)=\sum_{k=0}^n k \frac{n !}{k !(n-k) !} p^k q^{n-k}=\sum_{k=1}^n \frac{n !}{(k-1) !(n-k) !} p^k q^{n-k} \\ & =n p \sum_{k=1}^n \frac{(n-1) !}{(k-1) !(n-k) !} p^{k-1} q^{n-1-(k-1)} \\ & \end{aligned}

(3) 因为 X∼P(λ)X \sim P(\lambda), 所以 P(X=k)=λkk!e−λ,k=0,1,2,⋯P(X=k)=\frac{\lambda^k}{k !} e^{-\lambda}, k=0,1,2, \cdots. 由期望的定义得

E(X)=∑k=0nkλkk!e−λ=λe−λ∑k=1nλk−1(k−1)!\begin{aligned} & E(X)=\sum_{k=0}^n k \frac{\lambda^k}{k !} e^{-\lambda}=\lambda e^{-\lambda} \sum_{k=1}^n \frac{\lambda^{k-1}}{(k-1) !} \\ & \end{aligned}

例设有连续型随机变量 XX ，在下列三种情况下计算随机变量 XX 的数学期望 E(X)E(X) (1) X∼U(a,b)X \sim U(a, b); (2) X∼E(λ)X \sim E(\lambda); (3) X∼N(μ,σ2)X \sim N\left(\mu, \sigma^2\right).

解 (1) 因为 X∼U(a,b)X \sim U(a, b) ，所以 XX 的密度函数为

f(x)={1b−a,a<x<b,0, 其他. f(x)= \begin{cases}\frac{1}{b-a}, & a<x<b, \\ 0, & \text { 其他. }\end{cases}

由期望的定义得

E(X)=∫−∞+∞xf(x)dx=∫abxb−adx=a+b2E(X)=\int_{-\infty}^{+\infty} x f(x) d x=\int_a^b \frac{x}{b-a} d x=\frac{a+b}{2}

(2) 因为 X∼E(λ)X \sim E(\lambda) ，所以 XX 的密度函数为

f(x)={λe−λx,x>0,0,x≤0.f(x)= \begin{cases}\lambda e^{-\lambda x}, & x>0, \\ 0, & x \leq 0 .\end{cases}

由课前导读中的积分公式 1 得

E(X)=∫−∞+∞xf(x)dx=∫0+∞xλe−λxdx=λ⋅1!λ2=1λ 或 =−xe−λx∣0+∞+∫0+∞e−λxdx=−1λe−λx∣0+∞=1λ\begin{array}{r} E(X)=\int_{-\infty}^{+\infty} x f(x) d x=\int_0^{+\infty} x \lambda e^{-\lambda x} d x=\lambda \cdot \frac{1 !}{\lambda^2}=\frac{1}{\lambda} \\ \text { 或 }=-\left.x e^{-\lambda x}\right|_0 ^{+\infty}+\int_0^{+\infty} e^{-\lambda x} d x=-\left.\frac{1}{\lambda} e^{-\lambda x}\right|_0 ^{+\infty}=\frac{1}{\lambda} \end{array}

（3）因为 X∼N(μ,σ12)X \sim N\left(\mu, \sigma_1^2\right) 所以 XX 的密度函数为

f(x)=12πσe−(x−μ)22σ2f(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}

由期望的定义得

E(X)=∫−∞+∞x12πσe−(x−μ)22σ2dx= 今े t=x−μσ∫−∞+∞(σt+μ)12πσe−t22⋅σdt=μE(X)=\int_{-\infty}^{+\infty} x \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} d x \stackrel{\text { 今े } t=\frac{x-\mu}{\sigma}}{=} \int_{-\infty}^{+\infty}(\sigma t+\mu) \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{t^2}{2}} \cdot \sigma d t=\mu

上式使用了密度函数的规范性

例 一工厂生产的某种设备的寿命 XX（以年计）服从以 14\frac{1}{4} 为参数的指数分布，工厂规定，出售的设备若在售出一年之内损坏可予以调换，若工厂售出一台设备赢利 100 元，调换一台设备厂方需花费 300 元．求该工厂出售一台设备净贏利的数学期望．

解 因为 XX 服从以 14\frac{1}{4} 为参数的指数分布，所以分布函数为

F(x)={1−e−14x,x>0,0,x⩽0.F(x)= \begin{cases}1-\mathrm{e}^{-\frac{1}{4} x}, & x>0, \\ 0, & x \leqslant 0 .\end{cases}

一台设备在一年内损坏的概率为 P{X<1}=F(1)=1−e−14P\{X<1\}=F(1)=1-\mathrm{e}^{-\frac{1}{4}} ，使用一年不损坏的概率为

P{X⩾1}=1−P{X<1}=1−(1−e−14)=e−14.P\{X \geqslant 1\}=1-P\{X<1\}=1-\left(1-\mathrm{e}^{-\frac{1}{4}}\right)=\mathrm{e}^{-\frac{1}{4}} .

设 YY 表示出售一台设备的净赢利，其分布律如下． 图片

 故 E(Y)=(−200)×(1−e−14)+100×e−14=300e−14−200≈33.64 (元) . \begin{aligned} &\text { 故 }\\ &E(Y)=(-200) \times\left(1-\mathrm{e}^{-\frac{1}{4}}\right)+100 \times \mathrm{e}^{-\frac{1}{4}}=300 \mathrm{e}^{-\frac{1}{4}}-200 \approx 33.64 \quad \text { (元) . } \end{aligned}

概率分布表

下面列出了常见的概率分布表，

图片

在附录里，附带了常见的概率分布表，详见 此处

上一章1._本章思维导图
下一章3._随机变量函数的数学期望