10._卡方分布χ²-独立检验-Part1

自由度

在介绍三大分布之前，我们先说一下自由度。

从方程理解自由度

假设有一个3元函数 $x+y+z=1 ...(1)$

在这个等式里，可以改写为 $x=1-y-z$ 这意味着，虽然方程有3个未知量（变量能随便取值的数量称呼自由度），但是因为和为1，这使得，每给定一对 $(y,z)$ ，那么 $x$ 也就固定了，所以 $x$ 并不能随便取值，因此，我们说他的自由度为：2.

如果在增加一个限制 $y=2z ...(2)$

这样，每随意给 $z$ 一个值， $y$ 就固定了，而再由（1）知道 $x$ 也会固定，因此他的自由度为：1

换句话说，增加一个等式，会使得自由度减少。

卡方检验χ²的引入

χ²分布是由阿贝(Abbe)于1863年首先提出的，后来由海尔墨特(Hermert)和现代统计学的奠基人之一的卡·皮尔逊(C K．Pearson)分别于1875年和1900年推导出来。

χ²分布的主要用途，其实不是拿来用于自然现象的建模，而是用于假设检验用的。

Pearson在1900年提出χ²的论文，其实介绍的是χ²检验中的拟合优度检验。卡方检验主要用于分析两个分类变量的相关关系.

独立检验

我们通过一个简单例子来理解独立检验的实际意义。在许多实际问题中，我们需要考察两个分类变量之间是否有关系。例如，考察患肺癌与吸烟之间是否有关系。

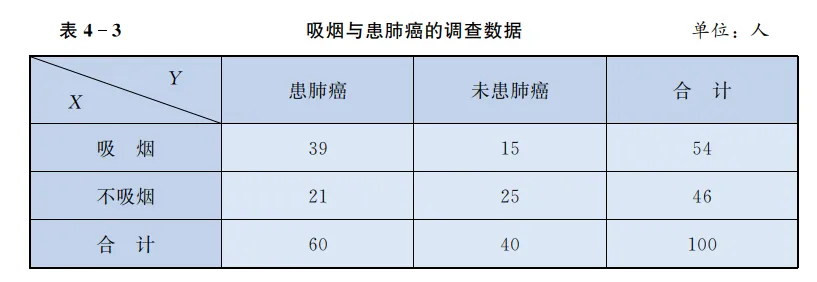
为了了解患肺癌与吸烟之间的关系，某医疗机构调查了其他条件都基本相同的 100 个人，调查结果如下表（表中 $X$ 表示＂是否吸烟＂， $Y$ 表示＂是否患肺癌＂）。 $图片$ {width=600px}

像上表这样，将两个分类变量进行交叉分类得到的频数分布表称为列联表；称 $X, Y$ 为分类变量，其中变量 $X$ 有两个变量值——＂吸烟＂和＂不吸烟＂，变量 $Y$ 有两个变量值——＂患肺癌＂和＂未患肺癌＂。

由于所涉及的两个分类变量 $X, Y$ 均有两个变量值，所以称上表为 $2 \times 2$ 列联表．

从表 4－3 可以得出，在 54 个吸烟的人中有 39 人患肺癌，患者占 $39 / 54 \approx$ $72.22 \%$ ；在不吸烟的 46 人中，有 21 人患肺癌，患者占 $21 / 46 \approx 45.65 \%$ 。吸烟者中患肺癌的比例比不吸烟者中患肺癌的比例高出约

72.22-45.65=26.57 \text { (个百分点). }

这种差异似乎已经说明吸烟与患肺癌有很大关系。但仔细想想，由于这 100 人是随机选取的，会不会是由于随机抽样的误差，使得所抽取的 60 名肺癌患者中碰到了较多的吸烟者，而在 40 名未患肺癌者中碰到了较多的不吸烟者？这样也可能导致吸烟者中肺癌患者的比例比不吸烟者中肺癌患者的比例高。

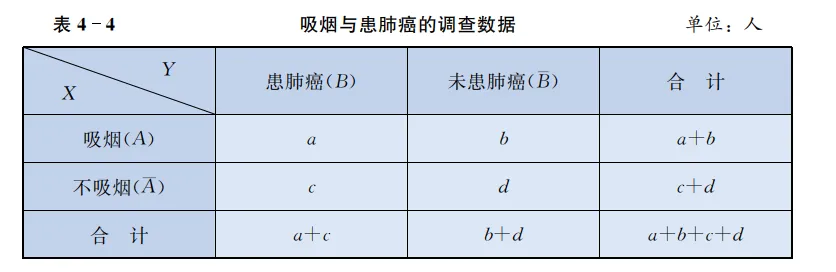
于是，我们还需进一步用统计方法来检验，因为单凭随机抽样的误差可能还不足以造成如此大的差异。为了讨论的方便我们引人以下记号：变量 $X: A=$ 吸烟， $\bar{A}=$ 不吸烟；变量 $Y: B=$ 患肺癌, $\bar{B}=$ 未患肺癌．我们将表 4－3 中的数字用字母代替得到如下列联表： $图片$ {width=600px}

在本案例中，

\begin{aligned} & a=39, b=15, c=21, d=25 \\ & n=a+b+c+d=100 \\ & a+b=54 \\ & c+d=46 \\ & a+c=60 \\ & b+d=40 \\ \end{aligned}

为分析 $X, Y$ 是否有关系，我们先提出假设

$H_0: X, Y$ 之间没有关系（独立） ,

，也就是假设＂吸烟 $(A)$ ＂与＂患肺癌 $(B)$ ＂独立．这时 $A$ 与 $B$ 独立， $\bar{A}$ 与 $B$ 独立， $A$ 与 $\bar{B}$ 独立， $\bar{A}$ 与 $\bar{B}$ 独立．

于是 $P(A \cap B)=P(A) P(B)$ 吸烟和患肺癌， $P(\bar{A} \cap B)=P(\bar{A}) P(B)$ 不吸烟和患肺癌， $P(A \cap \bar{B})=P(A) P(\bar{B})$ 吸烟和不患肺癌， $P(\bar{A} \cap \bar{B})=P(\bar{A}) P(\bar{B})$ 不吸烟和不患肺癌

根据概率与频率的关系，知道 $P(A \cap B)$ 的估计值为 $p_{A B}=\frac{a}{n}=0.39$ ,

$P(\bar{A} \cap B)$ 的估计值为 $p_{\bar{A} B}=\frac{c}{n}=0.21$ ,

$P(A \cap \bar{ B })$ 的估计值为 $p_{A \bar{B}}=\frac{b}{n}=0.15$ ,

$P(\bar{A} \cap \bar{B})$ 的估计值为 $p_{\bar{A} \bar{B}}=\frac{d}{n}=0.25$ ．

又 $P(A)$ 的估计值为 $p_A=\frac{a+b}{n}=0.54$ , $P(\bar{A})$ 的估计值为 $p_\bar{A}=\frac{c+d}{n}=0.46$ ， $P(B)$ 的估计值为 $p_B=\frac{a+c}{n}=0.6$ , $P(\bar{B})$ 的估计值为 $p_\bar{B}=\frac{b+d}{n}=0.4$ ．

因为假设 $X, Y$ 独立，所以 $\mu_{A B}=\left|p_{A B}-p_A p_B\right|$ $\mu_{\bar{A} B}=\left|p_{\bar{A} B}-p_\bar{A} p_B\right|$ $\mu_{A \bar{B}}=$ $\left|p_{A \bar{B}}-p_A p_\bar{B}\right|$ $\mu_{\bar{A} \bar{B}}=\left|p_{\bar{A} \bar{B}}-p_\bar{A} p_\bar{B}\right|$

都相应比较小.

我们用 $\chi^2$ （读作＂卡方＂）表示 $\mu_{A B}, \mu_{\bar{A} B}, \mu_{A \bar{B}}, \mu_{\bar{A} \bar{B}}$ 的总体大小，记

\begin{aligned} \chi^2 & =\dfrac{n \mu_{A B}^2}{p_A p_B}+\dfrac{n \mu_{\bar{A} B}^2}{p_\bar{A} p_B}+\dfrac{n \mu_{A \bar{B}}^2}{p_A p_\bar{B}}+\dfrac{n \mu_{\bar{A} \bar{B}}^2}{p_\bar{A} p_\bar{B}} \\ & =\frac{n(a d-b c)^2}{(a+b)(c+d)(a+c)(b+d)} . \end{aligned}

当 $\chi^2$ 的取值较小时，表示假设 $H_0$ 成立，当 $\chi^2$ 的取值较大时，表示假设 $H_0$ 不成立。

在本案例中，经过计算得到 $\chi^2$ 的观测值为

\chi^2=\frac{100(39 \times 25-15 \times 21)^2}{54 \times 46 \times 60 \times 40} \approx 7.307

那么， $\chi^2=7.307$ 这个取值是较大还是较小呢？

统计学家已经有明确的结论：如果 $2 \times 2$ 列联表中的两个分类变量 $X, Y$ 是独立的，即在 $H_0$ 成立的情况下，且当随机调查的数据 $a, b, c, d$ 都不小于 5 时，随机事件＂ $\chi^2 \geqslant 6.635$ ＂发生的概率约为 0.01 ，

即

P\left(\chi^2 \geqslant 6.635\right) \approx 0.01

也就是说，在 $H_0$ 成立的情况下， $\chi^2$ 的观测值大于或等于 6.635 的概率非常小，近似于 0.01 。即在 $H_0$ 成立的情况下，观测值超过 6.635 的概率不大于 0.01 ．

在本案例中，由抽样数据所得到的 $\chi^2 \approx 7.307>6.635$ ，这表明这一事件发生的概率不大于 0.01 ，这是一个小概率事件。因此，我们有 $\left[1-P\left(\chi^2 \geqslant 6.635\right)\right] \times$ $100 \%=99 \%$ 的把握认为 $H_0$ 不成立，于是否定假设 $H_0$ ，从而认为吸烟与患肺癌之间有关系。

值得指出的是，我们在作出上述判断时也有可能犯错误，因为吸烟与患肺癌没有关系时， $\chi^2$ 的观测值仍有可能超过 6.635 ．但是这一事件发生的概率不超过 0.01 ，也就是说，我们犯错误的概率不会超过 0.01 。

上面这种利用统计量 $\chi^2$ 来确定在多大程度上可以认为＂两个分类变量有关系＂的方法，称为两个分类变量的独立性检验．

卡方分布

通过上面可以看到，卡方分布的核心计算是：

\boxed{ \sum \dfrac{(\text { 观察值 }- \text { 预期值 })^2}{\text { 预期值 }} }

这就是皮尔逊发布的著名的卡方 $\chi^2$ 统计量

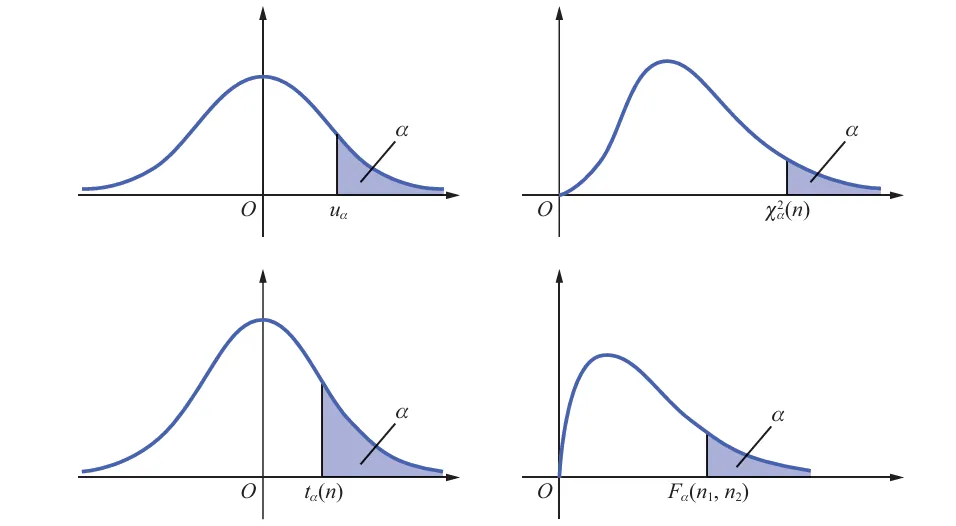
上 $\alpha$ 分位数

在数理统计中，对于已知分布和概率 $\alpha$ ，求实数 $x_\alpha$ 满足 $P\left\{X>x_\alpha\right\}=\alpha$ 的问题非常常见，其中 $x_\alpha$ 称为上侧 $\alpha$ 分位数（点），定义如下．具体解释参考附录置信区间和上a分位数

设有随机变量 $X$ ，对给定的 $\alpha(0<\alpha<1)$ ，若存在实数 $x_\alpha$ 满足

P\left\{X>x_\alpha\right\}=\alpha

则称 $x_\alpha$ 为 $X$ 的上侧 $\alpha$ 分位数（点）．

标准正态分布、自由度为 $n$ 的卡方分布、自由度为 $n$ 的 $t$ 分布、自由度为 $n_1, n_2$ 的 $F$ 分布的上侧 $\alpha$ 分位数分别记为 $u_\alpha, \chi_\alpha^2(n), t_\alpha(n), F_\alpha\left(n_1, n_2\right)$ ，图形如图所示。即有（1） $X \sim N(0,1)$ ，则 $P\left\{X>u_\alpha\right\}=\alpha$ ；（2） $\chi^2 \sim \chi^2(n)$ ，则 $P\left\{\chi^2>\chi_\alpha^2(n)\right\}=\alpha$ ；（3） $T \sim t(n)$ ，则 $P\left\{T>t_\alpha(n)\right\}=\alpha$ ；（4） $F \sim F\left(n_1, n_2\right)$ ，则 $P\left\{F>F_\alpha\left(n_1, n_2\right)\right\}=\alpha$ ．

$图片$

卡方检验的逻辑

聪明的同学可能已经发现了，卡方检验的方法其实就类似于反证法．

实际上，这两者既有联系也有区别．卡方检验先假设两变量独立，然后构造一个事件（具体来说该事件指的是皮尔逊检验统计量 $\chi^2$ 大于给定显著性水平 $\alpha$ 下的临界值），它在我们的假设之下发生的概率极小（即为 $\alpha$ ）。如果它在实际情况中发生了，就与小概率原理矛盾，因此我们便可以拒绝原假设。这个过程和反证法的步骤是类似的．具体参考下一节，拟合度检验。