经验分布函数
设总体 X 的分布函数为 F(x),X1,X2,⋯,Xn 是来自总体 X 的样本,若将样本观测值 x1,x2,⋯,xn 由小到大进行排列,记为 x(1)⩽x(2)⩽⋯⩽x(n) ,则称 X(1),X(2),⋯,X(n) 为有序样本.定义函数
Fn(x)=⎩⎨⎧0,k/n,1,x<x(1)x(k)⩽x<x(k+1),k=1,2,⋯,n−1x⩾x(n) 称 Fn(x) 为经验分布函数.显然 Fn(x) 是一非减右连续函数,且满足 Fn(−∞)=0 和 Fn(+∞)=1 .
【例 6.2.1】 某食品厂生产听装饮料,现在从生产线上随机抽取 5 听饮料,称得其净重为 (单位: g )
347351355351344. 求其经验分布函数.
解 经排序可得有序样本:
x(1)=344,x(2)=347,x(3)=351,x(4)=351,x(5)=355, 其经验分布函数为
F(n)=⎩⎨⎧0,0.2,0.4,0.8,1,x<344,344⩽x<347,347⩽x<351,351⩽x<355,x⩾355. 对于经验分布函数 Fn(x) ,格里汶科(Glivenko)在 1933 年证明了以下结果.
定理 (格里纹科定理)设 X(1),X(2),⋯,X(n) 是取自总体分布函数为 F(x) 的样本, Fn(x) 是其经验分布函数,当 n→∞ 时,有
P(−∞<x<∞sup∣Fn(x)−F(x)∣→0)=1 格里纹科定理表明:当 n 相当大时,经验分布函数是总体分布函数 F(x) 的一个良好的近似.证明 略。
6.2.2 频数-频率分布表
通过观察或试验得到的样本值一般都是杂乱无章的,通常没有什么价值,需要进行整理才能从总体上呈现其统计规律性.样本数据的整理是统计研究的基础,频数分布表或频率分布表是整理数据的常用方法.以下面的例子来介绍.
6.2.2 从贵州某高校中随机抽取 30 名学生,为了研究其月生活费情况,收集了这 30 学生未经整理的月生活费,如表6.2.1所示。
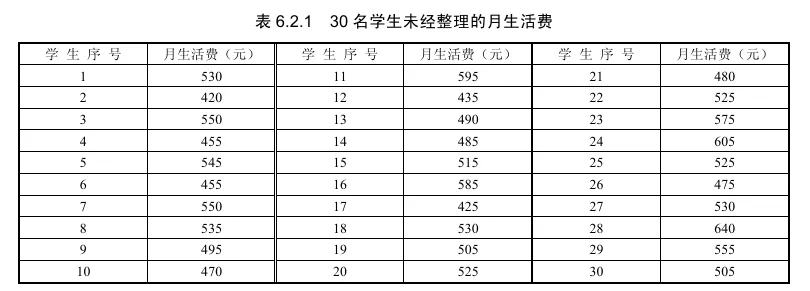
以下以例 6.2.2 为例介绍频数分布表的制作方法.表 6.2.1 是 30 名学生月生活费的原始资料,这些观测数据可以记为 x1,x2,⋯,x30 ,数据整理的具体步骤如下.
(1)对样本进行分组
首先确定组数 k ,作为一般性的原则,组数通常为 5∼20 个.对容量较小的样本,通常将其分为 5 组或者 6 组,容量为 100 左右的样本可以分为 7∼10 组,容量为 200 左右的样本可以分为 9∼13 组,容量为 300 左右及以上的样本可分为 12∼20 组,目的是使用足够的组数来表示数据的变异.本例只有 30 个数据,将之分为 5 组,即 k=5 .
(2)确定每组组距
每组区间的长度可以相同也可以不相同,在实际中常选用长度相同的区间方便进行比较,各组区间长度称为组距.样本观测值 x1,x2,⋯,xn 中的最小观测值为 x(1) ,最大观测值为 x(n) ,其近似公式为
组距 d=( 最大观测值 x(n)− 最小观测值 x(1))/ 组数.
本例中,数据最大观测值为 640 ,最小观测值为 420 ,故组距近似为
d=(640−420)/5=44 为方便,取组距为 50 .
(3)确定每组组限
各组区间端点为:a0,a0+d=a1,a0+2d=a2,⋯,a0+kd=ak .
各分组区间为:(a0,a1],(a1,a2],⋯,(ak−1,ak] ,其中,a0 略小于最小观测值,ak 略大于最大观测值。
本例中取 a0=400,a5=650 ,因此本例的分组区间为
(400,450],(450,500],(500,550],(550,600]),(600,650].
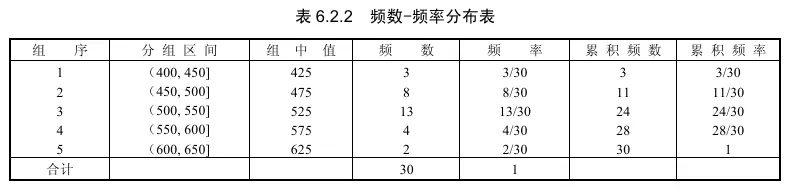
(4)列出频数-频率分布表
统计样本数据落入每个区间的个数——频数,然后列出其频数-频率分布表 6.2.2.
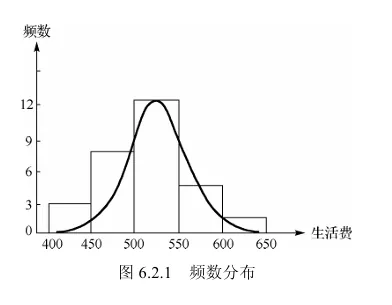
前面介绍了频数、频率的表格形式,它也可以用直方图表示,这在许多场合更直观。频数分布在组距相等的场合常用宽度相等的长条矩形表示,矩形的高低表示频数的大小.在图形上,它的横坐标表示所关心变量的取值区间,纵坐标表示频数,如图 6.2.1 所示.如果将纵坐标改成频率,则得到频率直方图.为使所有矩形面积和为 1 ,可将纵坐标表示频率/组距,如此得到的直方图称为单位频率直方图,或简称频率直方图.此三种直方图的差别仅在于纵轴刻度的选择,直方图本身并无变化.
用上述方法对抽取数据加以整理,编制频数分布表,作直方图,画出频率分布曲线,这就可以直观地看到数据分布的情况,在什么范围,较大较小的各有多少,在哪些地方分布得比较集中,以及分布图形是否对称等,所以,样本的频率分布是总体概率分布的近似.样本是总体的反映,但是样本所含的信息不能直接用于解决我们所要研究的问题,而需要把样本所含的信息进行数学上的加工,使其浓缩起来,从而解决问题.