一元线性回归模型
x 可以在一定程度上决定 y, 但由 x 的值不能准确地确定 y 的值. 为了研究它们的这种关系, 对 (x,y) 进行一系列观测, 得到一个容量为 n 的样本 ( x 取一组不完全相同的值): (x1,y1),(x2,y2),⋯,(xn,yn), 其中 yi 是 x=xi 处对随机变量 y 观察的结果. 每对 (xi,yi) 在直角坐标系中对应一个点, 把它们标在平面直角坐标系中, 称所得到的图为散点图. 如图 10.1.1 所示.
由图 10.1.1(a)可看出散点大致地围绕一条直线散布, 而图 10.1.1(b)中的散点大致围绕一条抛物线散布, 这就是变量间统计规律性的一种表现.
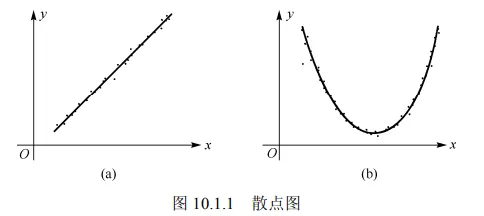
如果图中的点像图 10.1.1(a)中那样呈直线状, 则表明 y 与 x 之间有线性相关关系, 可建立数学模型
y=β0+β1x+ε...(10.1.1) 来描述它们之间的关系. 因为 x 不能严格地确定 y, 故有一误差项 ε, 假设 ε∼N(0,σ2), 相当于对 y 做这样的正态假设, 对于 x 的每一个值有 y∼N(β0+β1x,σ2), 其中未知数 β0、β1 不依赖于 x ,式(10.1.1)称为一元线性回归模型(Univariable Linear Regression Model)。
在式 (10.1.1) 中, β0、β1 是待估计参数. 由样本观察值可以获得 β0、β1 的估计 β^0 、 β^1, 称
y^=β^0+β^1x...(10.1.2) 为 y 关于 x 的经验回归函数,简称回归方程,其图形称为回归直线, β^1 称为回归系数. 对于给定 x=x0 后,称 y^0=β^0+β^1x0 为回归值(在不同场合也称其为拟合值和预测值)。
回归系数的最小二乘估计
样本的一组观察值 (x1,y1),(x2,y2),⋯,(xn,yn), 对每个 xi, 由线性回归方程(10.1.2)可以确定一回归值
y^i=β^0+β^1xi, 这个回归值 y^i 与实际观察值 yi 之差
yi−y^i=yi−β^0−β^1xi→yi−y^i=yi−(β^0+β^1xi) 刻画了 yi 与回归直线 y^=β^0+β^1x 的偏离度. 一个自然的想法就是:对所有 xi ,若 yi 与 y^i 的偏离越小, 则认为直线与所有试验点拟合得越好.
Q(β0,β1)=I=1∑n(yi−β0−β1xi)2, 记 β0 与 β1 的估计为 β^0、β^1, 若 β^0、β^1 满足
Q(β^0,β^1)=minQ(β0,β1), 则称 β^0、β^1 分别为 β0、β1 的最小二乘估计 (简记为 LSE).
对任意的 β0 与 β1, 都有 Q(β0,β1)⩾0, 且关于 β0、β1 的导数存在. 因此, 对 Q(β0,β1) 关
于 β0、β1 求偏导数, 并令其为零, 得
{∂β0∂Q=−2∑i=1n(yi−β0−β1xi)=0∂β1∂Q=−2∑i=1n(yi−β0−β1xi)xi=0, 整理得
{nβ0+(∑i=1nxi)β1=∑i=1nyi(∑i=1nxi)β0+(∑i=1nxi2)β1=∑i=1nxiyi, 称此为正规方程组, 解正规方程组得
{β^0=yˉ−xˉβ^1β^1=(∑i=1nxiyi−nxˉyˉ)/(∑i=1nxi2−nxˉ2),...(10.1.3) 其中 xˉ=n1∑i=1nxi,yˉ=n1∑i=1nyi ,若记
Lxy=i=1∑n(xi−xˉ)(yi−yˉ)=i=1∑nxiyi−nxˉyˉ,Lxx=i=1∑n(xi−xˉ)2=i=1∑nxi2−nxˉ2,...(10.1.14) 则
{β^0=yˉ−xˉβ^1β^1=Lxy/Lxx 式 (10.1.3) 或 (10.1.4) 称为 β0、β1 的最小二乘估计. 于是, 所求的线性回归方程为
y^=β^0+β^1x,...(10.1.5) 若将 β^0=yˉ−xˉβ^1 代入上式,则线性回归方程亦可表示为
y^=yˉ+β^1(x−xˉ)....(10.1.16) 式(10.1.6)表明,回归直线通过由样本观察值 (x1,y1),(x2,y2),⋯,(xn,yn) 确定的散点图的几何中心 (xˉ,yˉ). 回归直线是一条斜率为 β^1 且过点 (xˉ,yˉ) 的直线.
对于最小二乘估计, 还可以得到一个很重要的结论.
定理
若 β^0、β^1 为 β0、β1 的最小二乘估计, 则 β^0、β^1 分别是 β0、β1 的无偏估计, 且
β^0∼N(β0,σ2(n1+Lxxxˉ2)),β^1∼N(β1,Lxxσ2). 证明 略.
例 为了研究某一化学反应过程中温度 x 对产品得率 y 的影响.测得数据如下:

求产品得率 y 关于温度 x 的回归方程.
解 为了方便,列出如下的计算表格
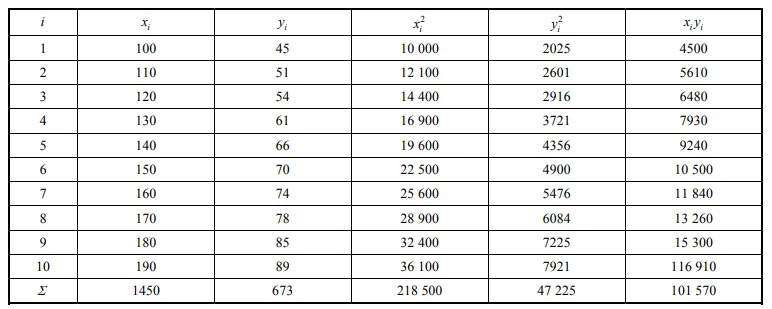
故 xˉ=101×1450=145,yˉ=101×673=67.3,
而
Lxx=i=1∑10xi2−10xˉ2=218500−10×(145)2=8250,Lxy=i=1∑10xiyi−10xˉyˉ=101570−10×145×67.3=3985, 从而 β^1=LxxLxy=82503980=0.483,β^0=yˉ−xˉβ^1=67.3−145×0.483=−2.735,
所以回归直线方程为 y^=−2.735+0.483x.
对于非线性问题转换为线性问题最常用的是取对数,例如 y=ex 这是一个指数函数,取对数后变为 lny=x,如果令y^=lny,x^=x ,则原本指数函数就会变成线性函数 y^=x^ ,在高中阶段学习的一元线性回归应用例题2 就演示了此方法


