10._边缘概率分布 - 概率论与数理统计

为什么引入边缘分布

引例1 前面介绍了联合分布，比如，我们要判定一个男生健康与否，需要通过“身高”和“体重”两个维度进行确定。但是对于有些活动，比如打篮球，我们更关注男生的身高（对于体重可以忽略），而对于有些活动比如矩阵，我们更关注男生的体重（身高可以忽略），换句话说，根据我们目的的不同，需要关注点也不同。因此引入了边缘分布。

引例2 考虑两个骰子的点数，第一个为 $X$ 第二个为 $Y$ 。那么 $p(X=1,Y=1)$ 就是扔出来 $(1,1）$ 的概率了，这个对应到连续的情况就是 $F(X=1,Y=1)$ ，这就是联合概率密度。那么我现在只关心第一个骰子，也就是 $X$ ，这时候 $p(X=1)$ 就包含了扔出来 $(X=1,Y=1)(1,2)......(1,6)$ 六个情况了，也就是“y等于多少都可以”，这个就对应到连续变量的边缘分布了。那么，你肯定清楚离散下从第一个概率算第二个就是把第一个概率求和，这个对应到连续就自然变成积分了。

边缘概率分布

边缘分布Marginal Distribution是指在多维随机变量的联合分布中，仅关注其中某一个或某几个变量的独立分布。也就是说，当我们有一个关于多个变量的联合概率分布时，我们可以通过对联合分布进行降维操作，得到只关于其中一个或某几个变量的概率分布，这个分布就是边缘分布。

定义

设 $(X, Y)$ 是一个二维随机变量，其联合分布为 $P(X, Y)$ 。

$X$ 的边缘分布是通过对 $Y$ 的所有可能取值求和（离散情况）或积分（连续情况）得到的：
离散情况： $P(X = x) = \sum_{y} P(X = x, Y = y)$
连续情况： $f_X(x) = \int_{-\infty}^{\infty} f_{X,Y}(x, y) \, dy$
类似地， $Y$ 的边缘分布为：
离散情况： $P(Y = y) = \sum_{x} P(X = x, Y = y)$
连续情况： $f_Y(y) = \int_{-\infty}^{\infty} f_{X,Y}(x, y) \, dx$

边缘分布函数 定义1 设二维随机变量 $(X, Y)$ 的联合分布函数为 $F(x, y)$ 称

F_X(x)=P(X \leq x)=P(X \leq x, Y<+\infty)=F(x,+\infty)

$-\infty<x<+\infty$ , 为随机变量 $X$ 的边缘分布函数；

称 $F_Y(y)=P(Y \leq y)=P(X<+\infty, Y \leq y)=F(+\infty, y)$ $-\infty<y<+\infty$ , 为随机变量 $Y$ 的边缘分布函数.

例 设二维随机变量 $(X, Y)$ 的联合密度函数为

f(x, y)=\left\{\begin{array}{cl} c y^2, & 0<x<2 y, 0<y<1, \\ 0, & \text { 其他. } \end{array}\right.

分别计算 $X$ 与 $Y$ 边缘分布函数. 解：在前面已得 $(X, Y)$ 的联合分布函数，

F(x, y)=\left\{\begin{array}{cc} 0, & x<0 \text { 或 } y<0 ; \\ \frac{2}{3} x\left(y^3-\frac{x^3}{32}\right), & 0 \leq x<2 y, \quad 0 \leq y<1 ; \\ \frac{2}{3} x\left(1-\frac{x^3}{32}\right), & 0 \leq x<2, \quad y \geq 1 ; \\ y^4, & x \geq 2 y, 0 \leq y<1 ; \\ 1, & x \geq 2, y \geq 1 . \end{array}\right.

故 $X$ 与 $Y$ 的边缘分布函数分别为

F_X(x)=F(x,+\infty)= \begin{cases}0, & x<0, \\ \frac{2}{3} x\left(1-\frac{x^3}{32}\right), & 0 \leq x<2, \quad F_Y(y)=F(+\infty, y)= \begin{cases}0, & y<0, \\ y^4, & 0 \leq y<1, \\ 1, & y \geq 1,\end{cases} \end{cases}

边缘分布的通俗解释

边缘分布可以理解为在多维随机变量中，忽略其他变量后，探寻某一维变量的分布情况。例如，在研究身高和体重的联合分布时，边缘分布可以分别描述身高或体重的单独分布。

你考虑扔两个骰子的点数，第一个为 $X$ ,第二个为 $Y$ 。那么 $P(X=1,Y=1)$ 就是扔出来 $(1,1)$ 的概率了，这个对应到连续的情况就是 $f(X=1,Y=1)$ ，这就是联合概率密度。

现在我只关心第一个色子，也就是 $X$ 的概率，这时候 $P(X=1)$ 就包含了扔出来 $(X=1,Y=1),(1,2)(1,3)(1,4)(1,5)(1,6)$ 六个情况了，也就是“Y等于多少都可以”，这个就对应到连续变量的边缘分布了。那么，你离散情况下从第一个概率算起，把第二个概率求和即可，这个对应到连续就自然变成积分，如果还不是很清楚，请看下面的例子：

离散型边缘分布

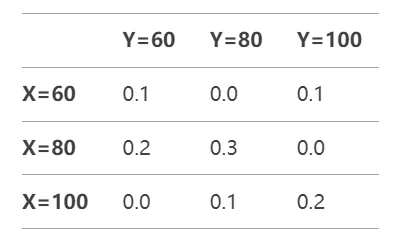
例 假设学生数学 $X$ 和语文 $Y$ 成绩的联合分布如下：这是一个学生成绩分布表，中间的一个数字表示该学生(语文和数学)的概率，比如该生语文80分，数学80分的概率0.3，语文100，数学80分的概率为0，现在，我们要研究该生数学为80的概率，只需要把X=80的数学对应的行加起来即可，即 0.2+0.3+0.0=0.5

$图片$

数学成绩 $X$ 的边缘分布

\begin{align*} P(X=60) &= 0.1 + 0.0 + 0.1 = 0.2, \\ P(X=80) &= 0.2 + 0.3 + 0.0 = 0.5, \\ P(X=100) &= 0.0 + 0.1 + 0.2 = 0.3. \end{align*}

语文成绩 $Y$ 的边缘分布

\begin{align*} P(Y=60) &= 0.1 + 0.2 + 0.0 = 0.3, \\ P(Y=80) &= 0.0 + 0.3 + 0.1 = 0.4, \\ P(Y=100) &= 0.1 + 0.0 + 0.2 = 0.3. \end{align*}

连续型边缘分布

相比离散型边缘分布，连续性边缘分布要难的多，这里的“难”不是说意义上的难，而是计算上的难。连续性边缘分布本质是广义积分，对于微积分不好的同学，计算积分是一大挑战。

不管是离散型还是连续性，边缘密度的定义都是一样的

设 $(X, Y)$ 是二维连续型随机变量，其概率密度为 $f(x, y)$ ，由定义可得 $X$ 的边缘分布函数

\begin{aligned} F_X(x) & =P(X \leqslant x)=P(X \leqslant x, y<+\infty) \\ & =\int_{-\infty}^x \int_{-\infty}^{+\infty} f(s, t) d s d t=\int_{-\infty}^x\left[\int_{-\infty}^{+\infty} f(s, t) d t\right] d s . \end{aligned}

进而可得 $X$ 的边缘密度函数为

f_X(x)=\frac{d F_X(x)}{d x}=\int_{-\infty}^{+\infty} f(x, y) d y .

同理， $Y$ 是连续型随机变量，且其边缘密度函数为

f_Y(y)=\int_{-\infty}^{+\infty} f(x, y) d x

分别称 $f_X(x)$ 和 $f_Y(y)$ 为 $(X, Y)$ 关于 $X$ 和 $Y$ 的边缘分布密度或边缘概率密度．

看懂连续性边缘分布图像

下图显示的 $F_X$ 边缘分布

$图片$

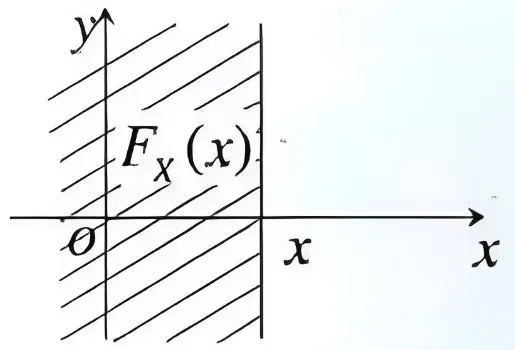
从图中可以看到，求 $X$ 边缘分布时，Y的取值范围是是 $(-\infty,+\infty)$

为了和联合分布对比，可以对比记忆，点击查看联合密度的密度图

例 设随机变量 $X$ 和 $Y$ 具有联合概率密度

f(x, y)=\left\{\begin{array}{ll} 6, & x^2 \leqslant y \leqslant x \\ 0, & \text { 其他 } \end{array} .\right.

求边缘概率密度 $f_X(x)$ 和 $f_Y(y)$ 。解

\begin{aligned} & f_X(x)=\int_{-\infty}^{+\infty} f(x, y) d y=\left\{\begin{array}{ll} \int_{x^2}^x 6 d y=6\left(x-x^2\right), & 0 \leqslant x \leqslant 1 \\ 0, & \text { 其他 } \end{array},\right. \\ & f_Y(y)=\int_{-\infty}^{+\infty} f(x, y) d x=\left\{\begin{array}{ll} \int_y^{\sqrt{y}} 6 d x=6(\sqrt{y}-y), & 0 \leqslant y \leqslant 1 \\ 0, & \text { 其他 } \end{array} .\right. \end{aligned}

例设平面区域 $D$ 由曲线 $y=\frac{1}{x}$ 及直线 $y=0, x=1, x= e ^2$ 所围成．二维随机变量 $(X$ ， $Y)$ 在区域 $D$ 上服从均匀分布，则 $(X, Y)$ 关于 $X$ 的边缘概率密度在 $x=2$ 处的值为 $\qquad$ 。解区域 $D$ 的面积

S_D=\int_1^{e^2} \frac{1}{x} d x=\left.\ln x\right|_1 ^{e^2}=2

所以二维随机变量 $(X, Y)$ 的联合分布密度为

f(x, y)= \begin{cases}\frac{1}{2}, & \text { 当 }(x, y) \in D \\ 0, & \text { 其他 }\end{cases}

则 $(X, Y)$ 关于 $X$ 的边缘概率密度

f_X(x)=\int_{-\infty}^{+\infty} f(x, y) d y=\int_0^{\frac{1}{x}} \frac{1}{2} d y=\frac{1}{2 x},\left.\quad f_X(x)\right|_{x=2}=\frac{1}{4}

故应填 $\frac{1}{4}$ ．