二维离散型举例
例 一家大型保险公司为一些客户提供服务,这些客户既购买了车险,又购买了财险。每种类型的保单都有一定的免赔额,车险的免赔额为 100 元或 250 元,财险的免赔额为 0 元、 100 元或 200 元。假设一个人同时购买了这两种保险,X 表示车险的免赔额,Y 表示财险的免赔额.根据该保险公司的历史数据可以得到随机变量 (X,Y) 的联合分布律如下.
 求:(1)客户财险的免赔额不低于 100 元的概率;(2)客户的免赔总额不超过 300 元的概率.
求:(1)客户财险的免赔额不低于 100 元的概率;(2)客户的免赔总额不超过 300 元的概率.
解(1)财险的免赔额不低于 100 元即随机变量 Y⩾100 ,包含了 Y=100 和 Y=200 两种情况,这里 X 在 100 和 250 中任意取值,故
200}P{Y⩾100}=P{X=100,Y=100}+P{X=100,Y=200}+P{X=250,Y=100}+P{X=250,Y==0.75 (2)免赔总额不超过 300 元即 X+Y⩽300 ,由题意可得其概率为
0}=P{X+Y⩽300}=P{X=100,Y=0}+P{X=100,Y=100}+P{X=100,Y=200}+P{X=250,Y=0.55 例设袋中有 4 个白球及 5 个红球, 现从中随机地抽取两次, 每次取一个, 定义随机变量 X、Y 如下:
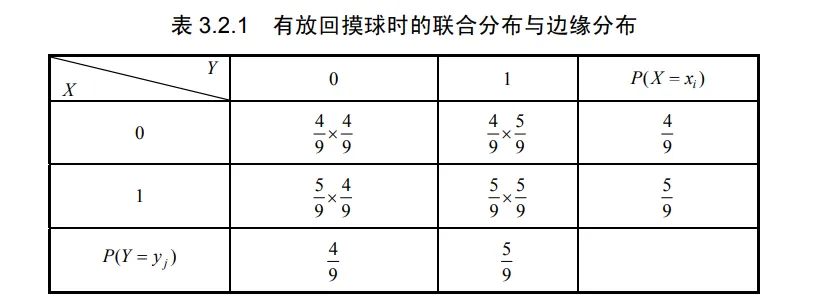
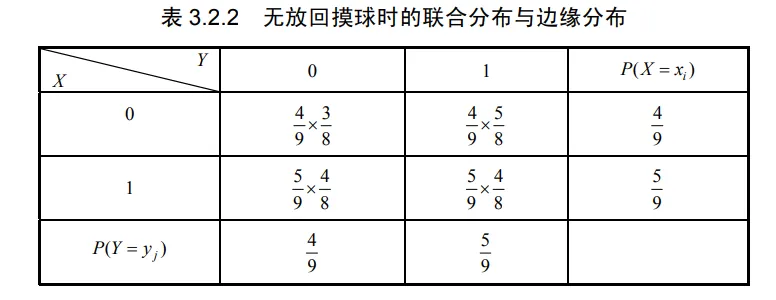
X={0,1, 第一次摸出白球 第一次摸出红球 Y={0,1, 第二次摸出白球 第二次摸出红球 . 写出下列两种试验的随机变量 (X,Y) 的联合分布与边缘分布.
(1)有放回摸球;(2)无放回摸球。
解 (1) 采取有放回摸球时, (X,Y) 的联合分布与边缘分布如表 3.2.1 所示.
 {widht=400px}
{widht=400px}
(2)无放回摸球。
 {widht=400px}
{widht=400px}
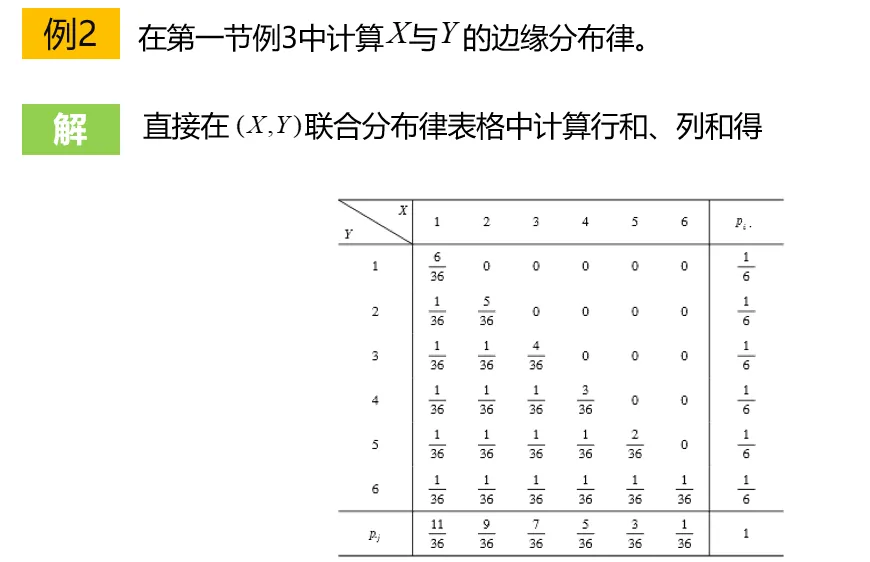
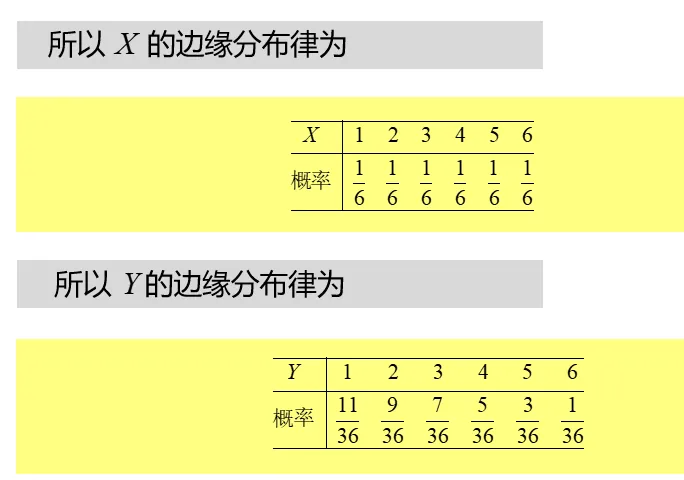
 求:(1)客户财险的免赔额不低于 100 元的概率;(2)客户的免赔总额不超过 300 元的概率.
求:(1)客户财险的免赔额不低于 100 元的概率;(2)客户的免赔总额不超过 300 元的概率. {widht=400px}
{widht=400px} {widht=400px}
{widht=400px}
