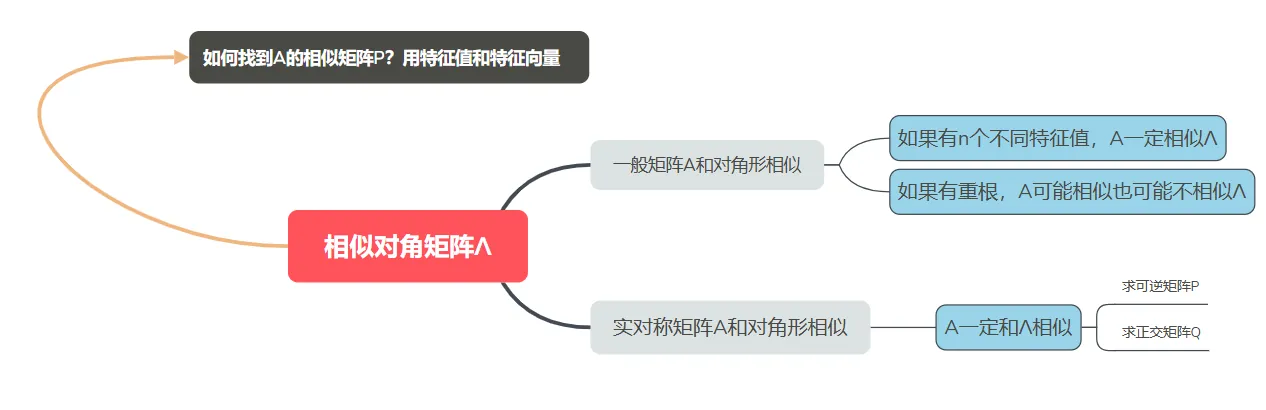
本章内容总体概述:假设有一头猪,我们要给他拍照,首先会选一个视角,这个视角就是矩阵(你也可以把这个矩阵理解为一个“参照物”),我们可以从不同视角给猪拍照,这些不同的视角和最初的视角是彼此相似的,如何找到不同的视角利用的就是特征值与特征向量。在这些视角里,会有一个比较好的视角(你可以理解为给猪正面拍照),这就是矩阵的对角化。 我们发现不是每个矩阵都可以对角化的,但是实对称矩阵一定可以对角化,所以,我们提出了正交相似(矩阵是一个微维表格,如果是对称矩阵,则他相当于对x , y x,y x , y
从上面的介绍,可以看到,在对矩阵的变换里,我们是层层推进的 (1)先找相似矩阵 (2)在找相似对角化 (3)再找对称矩阵的对角化 (4)再找行列式的值为1或者-1的对称矩阵的对角化,即正交矩阵。 而普通矩阵转为正交矩阵使用的是 施密特正交化工具。
知识总结 有时候我们学习的顺序和最终使用的目的正好相反。如果站在全局看本章内容,本章的核心是:对角形矩阵Λ \Lambda Λ ,即:任给一个矩阵A A A Λ \Lambda Λ
核心工具: 我们首先给出了特征值和特征向量,利用他可以找到矩阵A A A A A A
此时,矩阵分为两大类:一般矩阵A A A A A A
第一类: 一般矩阵A要和对角形Λ \Lambda Λ Λ \Lambda Λ 特征值的求法
(ii) 特征方程含有重根,此时A即可能相似对角形也可能不相似对角形,因此需要验证他的n个特征向量是否线性相关。 怎么验证呢?
假设在解特征方程 ∣ A − λ E ∣ = 0 |A- \lambda E|=0 ∣ A − λ E ∣ = 0 λ \lambda λ r r r r ( ∣ A − λ E ∣ ) r(|A- \lambda E|) r ( ∣ A − λ E ∣ ) n − r n-r n − r 思维导图版本2 的总结
第二类: 实对称矩阵A一定和对角形相似,此时考察的是2个重点:
(i) 让你求可逆矩阵P
这里只要求出他的特征值和对应的特征向量,然后把特征向量按照顺序排好,就可以得到他的可逆矩阵P P P 矩阵与对角形相似
(ii)让你求正交矩阵Q.
关于如何求Q Q Q P P P 正交变换 里介绍。本节仅是仅是介绍正交矩阵Q的基本概念,不会深入涉及 。
实对称矩阵的对角化 由前面介绍知道,一个 n n n n n n n n n n n n n n n P P P P − 1 A P = Λ P ^{-1} A P = \Lambda P − 1 A P = Λ Q Q Q Q − 1 A Q = Q T A Q = Λ Q ^{-1} A Q = Q^{ T } A Q= \Lambda Q − 1 A Q = Q T A Q = Λ
实对称矩阵具有非常优良的性质,他是线性代数里最为重要的矩阵。不是每个矩阵都可以对角化,但是实对称矩阵一定可以对角化。
下面我们不加证明引入一个重要结论
定理 设 A A A n n n Q Q Q
Q − 1 A Q = Λ = [ λ 1 λ 2 ⋱ λ n ] Q ^{-1} A Q = \Lambda =\left[\begin{array}{llll}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \ddots & \\
& & & \lambda_n
\end{array}\right] Q − 1 A Q = Λ = λ 1 λ 2 ⋱ λ n 为对角阵,其中 λ 1 , ⋯ , λ n \lambda_1, \cdots, \lambda_n λ 1 , ⋯ , λ n A A A Q T = Q − 1 Q^{T}=Q^{-1} Q T = Q − 1
上面这个结论告诉我们,任给一个实对称矩阵A A A Q Q Q Q Q Q Q − 1 A Q = Q ⊤ A Q = Λ Q^{-1} A Q=Q^{\top} A Q=\Lambda Q − 1 A Q = Q ⊤ A Q = Λ
如果你比较上面最后一个等式,即
Q − 1 A Q = Q ⊤ A Q = Λ Q^{-1} A Q=Q^{\top} A Q=\Lambda Q − 1 A Q = Q ⊤ A Q = Λ Q − 1 = Q T Q^{-1}=Q^{T} Q − 1 = Q T 也就是我们找到的这个矩阵Q同时满足了他的转置等于他的逆 。
实对称矩阵的性质 性质1 n n n n n n
性质2 实对称矩阵的特征向量互相正交。
证明:设 A \boldsymbol{A} A λ 1 \lambda_1 λ 1 λ 2 \lambda_2 λ 2 A \boldsymbol{A} A α 1 \boldsymbol{\alpha}_1 α 1 α 2 \boldsymbol{\alpha}_2 α 2 λ 1 \lambda_1 λ 1 λ 2 \lambda_2 λ 2
A α 1 = λ 1 α 1 , A α 2 = λ 2 α 2 . \boldsymbol{A} \boldsymbol{\alpha}_1=\lambda_1 \boldsymbol{\alpha}_1, \boldsymbol{A} \boldsymbol{\alpha}_2=\lambda_2 \boldsymbol{\alpha}_2 . A α 1 = λ 1 α 1 , A α 2 = λ 2 α 2 . 由
α 1 T A α 2 = α 1 T ( A α 2 ) = λ 2 α 1 T α 2 , α 1 T A α 2 = ( A α 1 ) T α 2 = λ 1 α 1 T α 2 , \begin{gathered}
\boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{A} \boldsymbol{\alpha}_2=\boldsymbol{\alpha}_1^{\mathrm{T}}\left(\boldsymbol{A} \boldsymbol{\alpha}_2\right)=\lambda_2 \boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2, \\
\boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{A} \boldsymbol{\alpha}_2=\left(\boldsymbol{A} \boldsymbol{\alpha}_1\right)^{\mathrm{T}} \boldsymbol{\alpha}_2=\lambda_1 \boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2,
\end{gathered} α 1 T A α 2 = α 1 T ( A α 2 ) = λ 2 α 1 T α 2 , α 1 T A α 2 = ( A α 1 ) T α 2 = λ 1 α 1 T α 2 , 知
( λ 1 − λ 2 ) α 1 T α 2 = 0. \left(\lambda_1-\lambda_2\right) \boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2=0 . ( λ 1 − λ 2 ) α 1 T α 2 = 0. 由于 λ 1 ≠ λ 2 \lambda_1 \neq \lambda_2 λ 1 = λ 2
α 1 T α 2 = ( α 1 , α 2 ) = 0 , \boldsymbol{\alpha}_1^{\mathrm{T}} \boldsymbol{\alpha}_2=\left(\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2\right)=0, α 1 T α 2 = ( α 1 , α 2 ) = 0 , 因此,特征向量 α 1 \boldsymbol{\alpha}_1 α 1 α 2 \boldsymbol{\alpha}_2 α 2
性质3 实对称矩阵必定相似对角形。
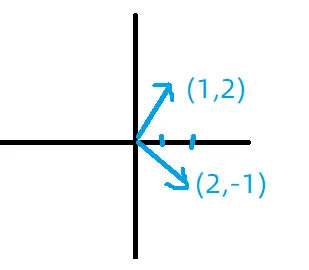
例当 A = [ 1 2 2 4 ] A=\left[\begin{array}{ll}1 & 2 \\ 2 & 4\end{array}\right] A = [ 1 2 2 4 ] p 1 = ( 2 , − 1 ) p_1=(2,-1) p 1 = ( 2 , − 1 ) p 2 = ( 1 , 2 ) p_2=(1,2) p 2 = ( 1 , 2 ) p 1 p_1 p 1 p 2 p_2 p 2
一个 2 × 2 2 \times 2 2 × 2 S = [ a b b c ] \quad S=\left[\begin{array}{ll}a & b \\ b & c\end{array}\right] S = [ a b b c ] x 1 = [ b λ 1 − a ] x _1=\left[\begin{array}{c}b \\ \lambda_1-a\end{array}\right] x 1 = [ b λ 1 − a ] x 2 = [ λ 2 − c b ] x _2=\left[\begin{array}{c}\lambda_2-c \\ b\end{array}\right] x 2 = [ λ 2 − c b ] x 1 x _1 x 1 x 2 x _2 x 2
实对称矩阵对角化的步骤如下 求特征值;
求特征向量;
将同一个特征值所对应的不同特征向量正交化(施密特正交化方法);
将所有正交特征向量规范化
得到 Q Q Q D D D
注意:本文涉及到后面的施密特正交化 ,建议学完后 正交矩阵 后,再来看本文
例 设 A = ( 4 2 2 2 4 2 2 2 4 ) A=\left(\begin{array}{lll}4 & 2 & 2 \\ 2 & 4 & 2 \\ 2 & 2 & 4\end{array}\right) A = 4 2 2 2 4 2 2 2 4 Q Q Q Q − 1 A Q = D Q^{-1} A Q=D Q − 1 A Q = D
第一步,是求特征值,
∣ A − λ I ∣ = ∣ 4 − λ 2 2 2 4 − λ 2 2 2 4 − λ ∣ = ∣ 8 − λ 8 − λ 8 − λ 2 4 − λ 2 2 2 4 − λ ∣ = ( 8 − λ ) ∣ 1 1 1 2 4 − λ 2 2 2 4 − λ ∣ = ( 8 − λ ) ∣ 1 1 1 0 2 − λ 2 0 0 2 − λ ∣ = ( 8 − λ ) ( 2 − λ ) 2 = 0 \begin{aligned}
|A-\lambda I| & =\left|\begin{array}{ccc}
4-\lambda & 2 & 2 \\
2 & 4-\lambda & 2 \\
2 & 2 & 4-\lambda
\end{array}\right|=\left|\begin{array}{ccc}
8-\lambda & 8-\lambda & 8-\lambda \\
2 & 4-\lambda & 2 \\
2 & 2 & 4-\lambda
\end{array}\right| \\
& =(8-\lambda)\left|\begin{array}{ccc}
1 & 1 & 1 \\
2 & 4-\lambda & 2 \\
2 & 2 & 4-\lambda
\end{array}\right|=(8-\lambda)\left|\begin{array}{ccc}
1 & 1 & 1 \\
0 & 2-\lambda & 2 \\
0 & 0 & 2-\lambda
\end{array}\right| \\
& =(8-\lambda)(2-\lambda)^2=0
\end{aligned} ∣ A − λ I ∣ = 4 − λ 2 2 2 4 − λ 2 2 2 4 − λ = 8 − λ 2 2 8 − λ 4 − λ 2 8 − λ 2 4 − λ = ( 8 − λ ) 1 2 2 1 4 − λ 2 1 2 4 − λ = ( 8 − λ ) 1 0 0 1 2 − λ 0 1 2 2 − λ = ( 8 − λ ) ( 2 − λ ) 2 = 0 我们得到特征值 λ 1 = 8 , λ 2 , 3 = 2 \lambda_1=8, \lambda_{2,3}=2 λ 1 = 8 , λ 2 , 3 = 2
当 λ = 8 \lambda=8 λ = 8
A − λ I = ( − 4 2 2 2 − 4 2 2 2 − 4 ) ∼ ( − 4 2 2 2 − 4 2 0 0 0 ) ∼ ( 2 − 4 2 − 4 2 2 0 0 0 ) ∼ ( 2 − 4 2 0 − 6 6 0 0 0 ) ∼ ( 2 − 4 2 0 1 − 1 0 0 0 ) ∼ ( 1 0 − 1 0 1 − 1 0 0 0 ) \begin{aligned}
A-\lambda I & =\left(\begin{array}{ccc}
-4 & 2 & 2 \\
2 & -4 & 2 \\
2 & 2 & -4
\end{array}\right) \sim\left(\begin{array}{ccc}
-4 & 2 & 2 \\
2 & -4 & 2 \\
0 & 0 & 0
\end{array}\right) \\
& \sim\left(\begin{array}{ccc}
2 & -4 & 2 \\
-4 & 2 & 2 \\
0 & 0 & 0
\end{array}\right) \sim\left(\begin{array}{ccc}
2 & -4 & 2 \\
0 & -6 & 6 \\
0 & 0 & 0
\end{array}\right) \\
& \sim\left(\begin{array}{ccc}
2 & -4 & 2 \\
0 & 1 & -1 \\
0 & 0 & 0
\end{array}\right) \sim\left(\begin{array}{ccc}
1 & 0 & -1 \\
0 & 1 & -1 \\
0 & 0 & 0
\end{array}\right)
\end{aligned} A − λ I = − 4 2 2 2 − 4 2 2 2 − 4 ∼ − 4 2 0 2 − 4 0 2 2 0 ∼ 2 − 4 0 − 4 2 0 2 2 0 ∼ 2 0 0 − 4 − 6 0 2 6 0 ∼ 2 0 0 − 4 1 0 2 − 1 0 ∼ 1 0 0 0 1 0 − 1 − 1 0 特征向量为 x ⃗ 1 = ( 1 1 1 ) \vec{x}_1=\left(\begin{array}{l}1 \\ 1 \\ 1\end{array}\right) x 1 = 1 1 1
当 λ = 2 \lambda=2 λ = 2
A − λ I = ( 2 2 2 2 2 2 2 2 2 ) ∼ ( 1 1 1 0 0 0 0 0 0 ) A-\lambda I=\left(\begin{array}{lll}
2 & 2 & 2 \\
2 & 2 & 2 \\
2 & 2 & 2
\end{array}\right) \sim\left(\begin{array}{lll}
1 & 1 & 1 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right) A − λ I = 2 2 2 2 2 2 2 2 2 ∼ 1 0 0 1 0 0 1 0 0 特征向量为 x ⃗ 2 = ( − 1 1 0 ) , x ⃗ 3 = ( − 1 0 1 ) \vec{x}_2=\left(\begin{array}{c}-1 \\ 1 \\ 0\end{array}\right), \vec{x}_3=\left(\begin{array}{c}-1 \\ 0 \\ 1\end{array}\right) x 2 = − 1 1 0 , x 3 = − 1 0 1
第四步,是通过施密特正交化,把他正交化,然后再单位化
(3)将 x ⃗ 1 , x ⃗ 2 , x ⃗ 3 \vec{x}_1, \vec{x}_2, \vec{x}_3 x 1 , x 2 , x 3 b ⃗ 1 = x ⃗ 1 , ∥ b ⃗ 1 ∥ = 3 \vec{b}_1=\vec{x}_1,\left\|\vec{b}_1\right\|=\sqrt{3} b 1 = x 1 , b 1 = 3 x ⃗ 1 \vec{x}_1 x 1 x ⃗ 2 , x ⃗ 3 \vec{x}_2, \vec{x}_3 x 2 , x 3
e ⃗ 1 = b ⃗ 1 ∥ b ⃗ 1 ∥ = ( 1 3 1 3 1 3 ) \vec{e}_1=\frac{\vec{b}_1}{\left\|\vec{b}_1\right\|}=\left(\begin{array}{c}
\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}} \\
\frac{1}{\sqrt{3}}
\end{array}\right) e 1 = b 1 b 1 = 3 1 3 1 3 1 我们对 x ⃗ 2 , x ⃗ 3 \vec{x}_2, \vec{x}_3 x 2 , x 3 b ⃗ 2 = x ⃗ 2 , ∥ b ⃗ 2 ∥ = 2 \vec{b}_2=\vec{x}_2,\left\|\vec{b}_2\right\|=\sqrt{2} b 2 = x 2 , b 2 = 2
e ⃗ 2 = b ⃗ 2 ∥ b ⃗ 2 ∥ = ( − 1 2 1 2 0 ) \vec{e}_2=\frac{\vec{b}_2}{\left\|\vec{b}_2\right\|}=\left(\begin{array}{c}
-\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} \\
0
\end{array}\right) e 2 = b 2 b 2 = − 2 1 2 1 0 x ⃗ 3 ⋅ b ⃗ 2 = 1 , ∥ b ⃗ 2 ∥ 2 = 2 \vec{x}_3 \cdot \vec{b}_2=1,\left\|\vec{b}_2\right\|^2=2 x 3 ⋅ b 2 = 1 , b 2 2 = 2
b 3 → = x ⃗ 3 − x ⃗ 3 ⋅ b ⃗ 2 ∥ b ⃗ 2 ∥ 2 b ⃗ 2 = ( − 1 0 1 ) − 1 2 ( − 1 1 0 ) = ( − 1 2 − 1 2 1 ) \overrightarrow{b_3}=\vec{x}_3-\frac{\vec{x}_3 \cdot \vec{b}_2}{\left\|\vec{b}_2\right\|^2} \vec{b}_2=\left(\begin{array}{c}
-1 \\
0 \\
1
\end{array}\right)-\frac{1}{2}\left(\begin{array}{c}
-1 \\
1 \\
0
\end{array}\right)=\left(\begin{array}{c}
-\frac{1}{2} \\
-\frac{1}{2} \\
1
\end{array}\right) b 3 = x 3 − b 2 2 x 3 ⋅ b 2 b 2 = − 1 0 1 − 2 1 − 1 1 0 = − 2 1 − 2 1 1 ∥ b ⃗ 3 ∥ = 3 2 , 将 b ⃗ 3 单位化。 e ⃗ 3 = b ⃗ 3 ∥ b ⃗ 3 ∥ = ( 1 6 − 2 6 1 6 ) 第四步, Q = ( e ⃗ 1 , e ⃗ 2 , e ⃗ 3 ) = ( − 1 2 1 3 1 2 1 2 1 3 − 2 6 0 1 3 1 6 ) , D = ( 8 2 2 ) \begin{aligned}
&\left\|\vec{b}_3\right\|=\sqrt{\frac{3}{2}}, \text { 将 } \vec{b}_3 \text { 单位化。 }\\
&\vec{e}^3=\frac{\vec{b}_3}{\left\|\vec{b}_3\right\|}=\left(\begin{array}{c}
\frac{1}{\sqrt{6}} \\
-\frac{2}{\sqrt{6}} \\
\frac{1}{\sqrt{6}}
\end{array}\right)\\
&\text { 第四步,}\\
&Q=\left(\vec{e}_1, \vec{e}_2, \vec{e}_3\right)=\left(\begin{array}{ccc}
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{\sqrt{2}}} & \frac{1}{\sqrt{3}} & -\frac{2}{\sqrt{6}} \\
0 & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}}
\end{array}\right), \quad D=\left(\begin{array}{ll}
8 & \\
& 2 \\
& 2
\end{array}\right)
\end{aligned} b 3 = 2 3 , 将 b 3 单位化。 e 3 = b 3 b 3 = 6 1 − 6 2 6 1 第四步, Q = ( e 1 , e 2 , e 3 ) = − 2 1 2 1 0 3 1 3 1 3 1 2 1 − 6 2 6 1 , D = 8 2 2 在《线性代数》里接下来应该介绍 正交矩阵和 正交相似,这部分内容涉及到向量,所以,转入到下一节里 正交矩阵
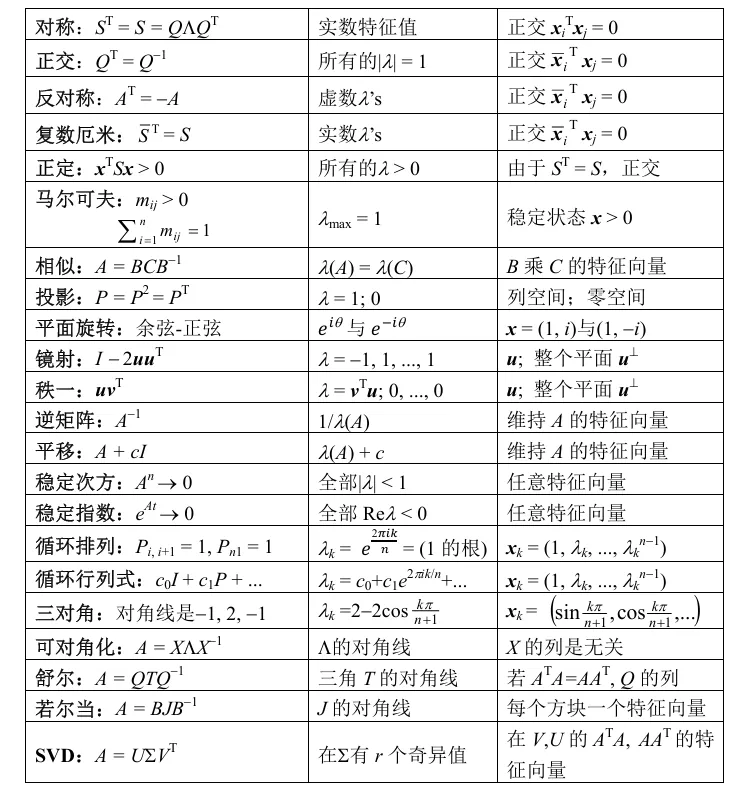
特征值与特征向量的矩阵性质总结