切比雪夫不等式
设随机变量 X 的数学期望 E(X) 及方差 D(X) 存在,则对于任意的 ε>0 ,有
P(∣X−E(X)∣≥ε)≤ε2D(X) 这就是切比雪夫不等式。
切比雪夫不等式的通俗解释
引例1
扔一个硬币求正面的概率。容易知道,他的概率是0.5,但是在实验时,有可能
①扔100次,正面的次数是48
②扔1000次,正面的次数490
③扔10000次,正面的次数为4800
④扔100000次,正面的次数为50001
可以发现,随着重复的次数越来越多,其正面的几率越来越接近期望值0.5。 我们把这种重复次数很多的数叫做“大数”
引例2
方差表示的数据离数学期望上下浮动的参数,例如张三和李四的立定跳远都是3m,张三的方差为0.0052,李四的方差为0.0082,可以看到,张三的成绩更稳定。因为方差本质反映数据的波动性。
定义
有了上面两个引例,就容易理解切比雪夫不等式了。切比雪夫不等式的意思是:
“随机变量X减去他的期望EX得绝对值”大于ε的概率 小于 方差除以ε2
我们把切比雪夫不等式拆开看。
(1)在中学就学过,∣x−a∣的绝对值表示x离开a的距离,因为有左右两个,所以加了绝对值。同样∣X−EX∣表示,样本值和他的期望值距离。 上面,张三跳远的平均值为3m,可能第一次跳 2.9米,第二次跳3.1米,不管是2.9米还是3.1米,样本值减去期望值后,误差都是0.1米(有绝对值,就不用考虑误差的正负了)。
(2)把∣X−EX∣当成一个整体考虑,那∣X−EX∣就表示每次跳远时,实际值和期望值的误差距离。比如上面张三第一次跳远的误差是0.1,第二次跳远误差是0.1,第三次跳远0.2,第四次跳远误差0.05,第五次跳远误差0.01等。可以看到,不管怎么跳,实际值总是在期望值左右来回摆动。
(3)在 P(∣X−EX∣)>ε 里, 微积分里已经学过ε表示一个无穷小量,比如取ε=0.1,则 P(∣X−EX∣>0.1)表示 张三跳远时,误差范围超过0.1的概率,也就是下图阴影部分的值
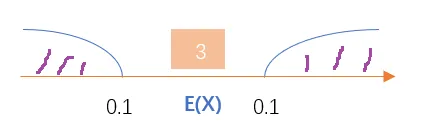
(4)切比雪夫不等式告诉我们,张三跳远时,误差范围超过0.1的概率 小于 ε2D(x)=0.121=0.120.0052=0.25%
假设取ε=0.2,可以计算张三跳远时,误差范围超过0.2的概率 小于 ε2D(x)=0.121=0.220.0052=0.062%
可以看到,ε取的越大,他的概率越小。这也很好理解,想象一下,张三跳远平均值是3米,取误差 ε=5,然后可以说,张三跳远误差超过5米的概率为0,这是没问题的。
我们说过切比雪夫不等式左边求的是上图阴影部分的概率,这就像射箭,靶心是数学期望,ε相当于误差的半径,当 允许的ε误差半径越大,则落在外面的概率越低。
切比雪夫还有一个等价公式(反向说法)即:
P{∣X−EX∣<ε}⩾1−ε2DX2 例如 取 ε=0.0001 (趋近于零),则1−ε2DX2就趋近于1(ε 在分母上). 然后我们可以说,张三跳远平均值为3,每次跳远误差超过0.0001的概率为100%,即张三每次跳远误差一定超过0.0001m
证明
仅给出 X 为连续型随机变量的证明。
P(∣X−E(X)∣≥ε)=∫∣x−ε(x)∣≥εf(x)dx≤∫∣x−E(x)∣∑εε2∣X−E(X)∣2f(x)dx≤∫−∞+∞ε2∣X−E(X)∣2f(x)dx=ε2D(X) 切比雪夫不等式作用
如果记数学期望EX=μ, 方差DX2=σ2, 利用切比雪夫不等式可以在未知随机变量 X 分布的情况下,估计 P{∣X−μ∣⩾ε} 或 P{∣X−μ∣<ε} 。例如,
P{∣X−μ∣<3σ}⩾1−9σ2σ2≈0.8889 P{∣X−μ∣<4σ}⩾1−16σ2σ2=0.9375. 由切比雪夫不等式可知当 σ2 越小时,P{∣X−μ∣<ε} 就越大,表明随机变量 X 的取值集中在 μ 的附近,进一步体现了 σ2 的意义.特别地,当 σ2=0 时,有下列推论:
推论 在切比雪夫不等式中,如果 σ2=0 ,则 P{X=EX}=1 .
证 如果 σ2=0 ,则由切比雪夫不等式知,对任意的 ε>0 ,有 P{∣X−μ∣<ε}⩾1 ,从而 P{∣X−μ∣<ε}=1 .考虑到 ε 的任意性,得 P{X=μ}=1 ,即 P{X=EX}=1 .
例题
例设 X∼N(μ,σ2) 计算 P(∣X−μ∣≥3σ) 。
解: 因为 σX−μ∼N(0,1) ,所以
P(∣X−μ∣≥3σ)=P(σX−μ≥3)P(σX−μ≥3)=2−2Φ(3)=0.003 例设 X∼N(μ,σ2) 用切比雪夫不等式估计概率 P(∣X−μ∣≥3σ) 。
解
因为 ε=3σ ,由切比雪夫不等式得
P(∣X−E(X)∣≥ε)≤ε2D(X)P(∣X−μ∣≥3σ)≤(3σ)2D(X)=91 点评 此类题型的求解方法比较单一,在随机变量 X 的期望 EX 和方差 DX 已知的情况下,直接应用切比雪夫不等式即可;若 EX 和 DX 未知,当根据题意并结合数学期望和方差的性质计算出 EX 和 DX ,然后再套用切比雪夫不等式.
例设随机变量 X 的方差 D(X)=0 ,求证, X 服从参数为 c 的退化分布。
证明 利用切比雪夫不等式得,对任意的 ε>0 ,有
0≤P(∣X−E(X)∣≥ε)≤ε2D(X)=0 由 ε 的任意性知
P(X=E(X))=1 例设随机变量 X 的标准化随机变量为 X∗=DXX−EX ,试根据切比雪夫不等式估计概率 P{∣X∗∣≤2} 。
解
P{∣X∗∣<2}=P{DXX−EX<2}=P{∣X−EX∣<2DX}⩾1−(2DX)2DX=43. 例已知正常男性成人血液中,每一毫升白细胞数平均是 7300 ,均方差是 700 ,利用切比雪夫不等式估计每毫升含白细胞数在 5200∼9400 之间的概率 p 。
解 假设正常男性成人血液中每毫升白细胞数为 X ,依题设 E(X)=7300,D(X)=7002 ,于是
P{5200<X<9400}=P{∣X−7300∣<2100}⩾1−210027002=98, 即每毫升含白细胞数在 5200∼9400 之间的概率不低于 98 .
例设电站供电网有 10000 个电灯,夜晚时每个电灯开灯的概率均为 0.7 ,假定所有电灯的开或关是相互独立的,试用切比雪夫不等式估计夜晚同时开着的电灯在 6800∼7200个的概率.
(解)令 X 表示在夜晚同时开着的电灯数,则 X 服从 n=10000,p=0.7 的二项分布,这时 E(X)=np=7000,D(X)=npq=2100 ,由切比雪夫不等式可得
P{6800<X<7200}=P{∣X−7000∣<200}⩾1−20022100≈0.95 这个概率的近似值表明,在 10000 个电灯中,开着的电灯在 6800∼7200 个的概率大于 0.95 .而实际上,此概率可由二项分布求得精确值为 0.99999 .由此可知,切比雪夫不等式虽可用来估计概率,但精度不够高.
