14._连续型_指数分布与无记忆性 - 概率论与数理统计

注：在概率论里，和连续分布相关的基本上都和“时间”相关，因为时间是连续的。泊松过程的三个重要分布在概率论和随机过程理论中经常出现，它们分别是：泊松分布（Poisson Distribution）：描述固定时间内发生事件的数量。指数分布（Exponential Distribution）：描述事件间隔时间的分布。伽马分布（Gamma Distribution）：描述多个事件发生时间的分布。点击他们的分布链接可以了解三者之间的区别和联系。

生活中，某个特定事件发生所需要的等待时间往往服从指数分布，例如，许多电子元件的使用寿命、电话的通话时间、母鸡下蛋的等待时间，球场等待进球的时间等都可以认为是服从指数分布的

指数分布

如果随机变量 $X$ 的密度函数为

f(x)=\left\{\begin{array}{cl} \lambda \mathrm{e}^{-\lambda x} & x>0 \\ 0 & \text { 其余 } \end{array}\right.

则称 $X$ 服从参数为 $\lambda$ 的指数分布，记为 $X \sim E(\lambda),(\lambda>0)$ .

指数分布的密度函数图像。 {width=300px}

指数分布的分布函数如下图

F(x)=\left\{\begin{array}{cc} 1-\mathrm{e}^{-\lambda x} & x \geq 0 \\ 0 & x<0 \end{array}\right.

{width=300px}

例设随机变量 $X$ 表示某餐馆从开门营业起到第一个顾客到达的等待时间（单位： $\min$ ），若 $X$ 服从指数分布，其概率密度为

f(x)= \begin{cases}0.4 e^{-0.4 x}, & x>0, ~ \\ 0, & \text { 其他. }\end{cases}

求等待至多 5 min 的概率以及等待 $3 \sim 4 min$ 的概率．解由题意知 $X$ 的分布函数为

F(x)= \begin{cases}1-e^{-0.4 x}, & x>0, \\ 0, & \text { 其他. }\end{cases}

可得

\begin{gathered} P\{X \leqslant 5\}=F(5)=1-e^{-2} \approx 0.865, \\ P\{3 \leqslant X \leqslant 4\}=F(4)-F(3)=e^{-1.2}-e^{-1.6} \approx 0.099 . \end{gathered}

例 设顾客在某银行窗口等待服务的时间（以分计） $X$ 服从指数分布，其概率密度函数为

f(x)=\left\{\begin{array}{cc} \frac{1}{5} e^{-x / 5} & x>0 \\ 0, & \text { 其它 } \end{array}\right.

求等待超过10分钟的概率。

解：某一次在窗口等待时间超过 10 分钟的概率记为 $P$ ，

P=\int_{10}^{+\infty}(1 / 5) e^{(-x / 5)} d x=e^{-2}

为什么我们必须发明指数分布？

在理解指数分布前，建议已经阅读了泊松分布。泊松分布是预测固定时间内发生事件的数量，比如网站每周有17个点赞，我想预测下周有10个人点赞的概率。所以泊松分布预测的时间间隔是固定的。

那为什么我们必须发明指数分布？答案是预测直到下一个事件（即成功，失败，到达等）的等待时间！例如，我们要预测以下内容的时间间隔：

电脑硬件出现故障的时间间隔
你需要等待直到公交车到达的时间间隔
餐馆开业第一个客人到来等待的时间价格

那么，我的下一个问题是：为什么直到发生下一个事件的时间概率密度是：

f_T(t)=\lambda \star e^{-\lambda t}

进一步的，后续问题将是：

X \backsim \operatorname{E}(0.25)

0.25 是什么意思？表示 0.25 分钟、小时或天，还是 0.25 个事件？

指数分布 $X \sim \operatorname{E}(\lambda)$ 中 $\lambda$ 与泊松分布中 $X \sim \operatorname{P}(\lambda)$ 的 $\lambda$ 相同吗？

请记住以下说明，为防止参数混淆， $X \sim \operatorname{E}(0.25)$ 中， 0.25 不是一个持续时间，它是一个事件速率，这与泊松过程参数 $\lambda$ 意义完全相同。

例如，您的博客每天有 500 位访问者，是一个事件速率，一小时内到达商店的顾客数量是一个速率，每年发生的地震数量是一个速率，一周内发生的车祸数量是一个速率，页面上的错字数量等都是时间单位内的速率，它是泊松分布的参数 $\lambda$ 。

指数分布里的 $\lambda$ 表示速率，即单位时间内事故发生的次数，但是我们日常生活中，对事件经过的建模，我们倾向于用时间间隔而不是速率来表示，例如，计算机可以正常开机的年数是 10 年（而不是说每年 0.1 次故障），飓风每 7 年出现一次（而不是说每年出现 $\frac{1}{7}$ ），客户每 10 分钟到达一次（而不是说每分钟 0.1 个顾客），依此类推。当您看到术语－指数分布的＂均值＂时，就是 $1 / \lambda$ ，这很好理解，只是为了表达方便。

当您看到术语＂衰减参数＂，或是术语＂衰减率＂时，就会开始困惑，该术语经常在指数分布中使用。所述衰减参数是用来表示时间（例如，每 10 分钟，每 7 年等），这是一个泊松分布速率参数 $(\lambda)$ 的倒数 $(1 / \lambda)$ 。想想看：如果您每小时获得 3 个客户 $(\lambda)$ ，则意味着您每 $1 / 3$ 小时获得1个客户（ $1 / \lambda$ ）意义相同。

因此，现在您可以回答以下问题：＂ $X \sim \operatorname{E}(0.25)$ ＂是什么意思？这意味着泊松速率为 0.25 。在单位时间内（一分钟，一小时或一年），该事件平均发生 0.25 次。将此转换为时间项，假设您的单位时间为一个小时，那么直到事件发生需要 4 个小时（倒数 0.25 的倒数）。

因此

1．指数参数 $\lambda$ 与泊松过程 $(\lambda)$ 相同 2．指数分布中经常讨论 $1 / \lambda$ 3． $1 / \lambda$ 代表下一次发生的时间间隔

让我们开始从头推出指数分布的密度公式(PDF)

我们的第一个问题是：为什么直到下一个事件发生时的时间的PDF为：

\lambda \cdot e^{-\lambda t}

指数分布概率分布研究的是泊松过程的事件之间的时间间隔。如果您考虑一下，那么直到事件发生的时间意味着在等待期间，没有一个事件发生。换句话说，这就是 Poisson（ $X = 0$ ）在泊松分布 $P(X=k)=\frac{\lambda^k \cdot e^{-\lambda}}{k!}$ 带入 $X=0$ 得 $P(X=0)=\frac{\lambda^0 \cdot e^{-\lambda}}{0!}=e^{-\lambda}$

关于泊松PDF要记住的一件事是，Poisson $(X=k)$ 发生的时间段仅为一个单位时间内。如果要对＂在持续时间 $t$ 内什么都没有发生＂的概率分布进行建模，而不仅仅是在一个单位时间内，您将如何做？

\begin{aligned} P & =P(\text { 在 } t \text { 时间间隔内什么都没发生 }) \\ & =P(X=0 \text { 第 } 1 \text { 间隔内 }) * P(X=0 \text { 第 } 2 \text { 间隔内 }) * \ldots * P(X=0 \text { 第 } t \text { 间隔内 }) \\ & =e^{-\lambda} * e^{-\lambda} \ldots e^{-\lambda} \\ & =e^{-\lambda t} \end{aligned}

处理思路像不像几何分布，其实这就是几何分布的微分形式而已

泊松分布假设事件彼此独立发生。因此，我们可以通过将 $P ( X =0$ 在单个时间单位内） $t$ 倍乘以计算在 $t$ 个时间单位内零成功的概率。

P(T>t)=P(X=0 \text { 在 } t \text { 个单位时间内 })=e^{-\lambda t}

$T$ ：我们感兴趣的随机变量：直到第一个事件发生的等待时间的随机变量。 $X$ ：遵循泊松分布的单位时间内事件的数量。 $P(T>t)$ ：直到第一个事件的等待时间大于 t 个时间单位的概率； $P(X=0$ ，以 $t$ 个时间单位）：以 $t$ 个时间单位发生事件数为零的概率

密度函数PDF是分布函数CDF的微分，由于我们已经有了CDF $(1－P(T>t))$ ，因此可以通过对其进行微分来获得PDF。

\begin{aligned} &P(T \leq t)=1-P(T>t)=1-e^{-\lambda t} \end{aligned}

由此即可得到指数分布的密度函数PDF

\begin{aligned} &\frac{d}{d t}(C D F)=\frac{d}{d t}\left(1-e^{-\lambda t}\right)=\lambda e^{-\lambda t} \end{aligned}

指数分布的无记忆特性

指数分布的无记忆特性可定义为：定义：

\boxed{ P(T>a+b \mid T>a)=P(T>b) }

这意味着，给定一个指数随机变量 $T$ ，在它已经超过第一个周期 $a$ 的情况下， $T$ 超过两个周期之和 $(a+b)$ 的概率等于 $T$ 只超过第二个周期 $b$ 的概率。

指数分布的无记忆如何证明？

\begin{gathered} P(T>t)=e^{-\lambda t} \\ P(T>a+b \mid T>a)=\frac{P(T>a+b)}{P(T>a)} \\ =\frac{e^{-\lambda(a+b)}}{e^{-\lambda a}} \\ =e^{-\lambda b} \\ P(T>t)=e^{-\lambda b} \end{gathered}

指数分布的无记忆是＂有用的＂属性吗？

使用指数分布对机械设备的寿命进行建模是否合理？例如，如果设备已经使用了 9 年，则无记忆意味着设备将再使用 3 年（总共 12 年）的概率与使用新机器在接下来的3年中的概率完全相同年份。

P(T>12 \mid T>9)=P(T>3)

这个方程对您来说看起来合理吗？对我们而言，事实并非如此。根据经验，设备越旧，发生故障的可能性就越大。为了对此特性建模（增加危险率），我们可以使用例如韦伯分布Weibull分布。

那么，什么时候使用指数分布（恒定风险率）合适呢？

车祸。你发生车祸的概率并不会因为你在过去五小时内是否没有发生过车祸而增加或减少。这就是 λ 经常被称为危险率的原因。

还有谁拥有无记忆的特性？

指数分布是唯一无记忆的连续分布。与之对应的离散分布--几何分布，是唯一无记忆的离散分布。下面是一些应用场景

a）等待时间建模指数型随机变量值的小值较多，大值较少。例如，您正在等的公交车可能会在接下来的 10 分钟内到达，而不是接下来的 60 分钟。

使用指数分布，我们可以回答以下问题：

公交车平均每 15 分钟到达一次。(假设从一辆公交车到下一辆公交车的时间呈指数分布，考虑到一小时内到达的公交车总数呈泊松分布，这就说得通了）。你刚刚错过了公交车！司机太不近人情了。你一到站，司机就关上车门开走了。如果下一班车在接下来的 10 分钟内没有到达，你就必须叫 DIDI，否则你就迟到了。下一班车在 10 分钟内到达的概率是多少？ 90% 的公交车在前一辆车之后多少分钟内到达？两辆公共汽车平均需要多长时间到达？ *如果您想查看答案是否正确，请在评论中发表您的答案。

b）可靠性（故障）建模由于我们可以对成功事件（总线的到达）进行建模，所以为什么不对失败建模（产品持续的时间）建模呢？

硬件需要重新启动之前可以运行的小时数平均以8,000小时（约一年）成倍地分配。

您没有备份服务器，并且需要不间断运行10,000小时。您无需重启服务器就能完成运行的可能性是多少？在12个月至18个月之间，服务器不需要重新启动的可能性是多少？请注意，有时候，当整个生命周期内故障率发生变化时，指数分布可能不合适。但是，它将是唯一具有这种独特属性（恒定危险率）的分布。

c）服务时间建模（排队论）代理商的服务时间也可以建模为指数分布变量。

一个过程的总长度（由几个独立任务组成的序列）遵循Erlang分布：几个独立的指数分布变量之和的分布。

回顾：泊松与指数分布之间的关系

如果每单位时间的事件数服从泊松分布，则事件之间的时间量遵循指数分布。假设事件之间的时间不受先前事件之间的时间影响（即它们是独立的），则每单位时间的事件数遵循泊松分布，比率为λ = 1 /μ。

指数分布的数学期望和方差

设随机变量 $X \sim \operatorname{Exp}(\lambda)$ ，则

E(X)=\int_0^{\infty} x \lambda e^{-\lambda x} d x=\int_0^{\infty} x d\left(-e^{-\lambda x}\right)=-\left.x e^{-\lambda x}\right|_0 ^{\infty}+\int_0^{\infty} e^{-\lambda x} d x=-\left.\frac{1}{\lambda} e^{-\lambda x}\right|_0 ^{\infty}=\frac{1}{\lambda}

在指数分布中, 有时记 $\theta=1 / \lambda$ , 则 $\theta$ 为指数分布的数学期望. 又因为

E\left(X^2\right)=\int_0^{\infty} x^2 \lambda e^{-\lambda x} d x=\int_0^{\infty} x^2 d\left(-e^{-\lambda x}\right)=-\left.x^2 e^{-\lambda x}\right|_0 ^{\infty}+2 \int_0^{\infty} x e^{-\lambda x} d x=\frac{2}{\lambda^2},

由此得 $X$ 的方差为

D(X)=E\left(X^2\right)-[E(X)]^2=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2} .

譬如, 某电子元件的寿命 (单位: h ) $X$ 服从指数分布 $\operatorname{Exp}(\lambda)$ , 其中 $\lambda=0.001$ , 则平均寿命为 $1000(h)$ , 方差为 $10^6\left(h^2\right)$ . 寿命数据的方差常是很大的.

关于更多概率分布表见附录1：常见概率分布表

关于对无记忆性在教材里的解读

在大部分《概率论与数理统计》教材里，包括贾书、茆书，在介绍指数分布时，都是用电子原件的寿命做例题：某指数分布是一种偏态分布, 由于指数分布随机变量只可能取非负实数, 所以指数分布常被用作各种 “寿命” 分布, 譬如电子元器件的寿命、动物的寿命、电话的通话时间、随机服务系统中的等待时间等都可假定服从指数分布. 指数分布在可靠性与排队论中有着广泛的应用.

例某元件的寿命 $X$ 服从参数为 $\lambda$ 的指数分布，已知其平均寿命为 1000 小时 $\left(\lambda=1000^{-1}\right)$ ，求 3 个这样的元件使用 1000 小时，至少已有一个损坏的概率．

解由题设知， $X$ 的分布函数为

F(x)= \begin{cases}1-e^{-\frac{x}{1000}}, & x \geqslant 0 \\ 0, & x<0\end{cases}

由此得到

P(X>1000)=1-P(X \leqslant 1000)=1-F(1000)=1-F(1000)=e^{-1}

各元件的寿命是否超过 1000 小时是独立的，用 $Y$ 表示 3 个元件中使用 1000 小时损坏的元件数，则 $Y \sim B\left(3,1- e ^{-1}\right)$ 。

所求概率为

P(Y \geqslant 1)=1-P(Y=0)=1-C_3^0\left(1-e^{-1}\right)^0\left(e^{-1}\right)^3=1-e^{-3}

对于初学者感觉最大的困惑是：指数分布的无记忆性和现实的体验完全相反。在教材里，说一个设备使用10年后再用5年出现故障的概率和新买的使用5年后出现故障的概率相同，这就是指数分布的无记忆性。但是现实总，很明显使用10年后出现故障的概率远大于新买的概率。那么问题到底出现在哪里呢？那就是：设备的老化。在数学里当使用指数分布时，他构建的是一个理想状态，即设备没有老化的现象，可是现实总，设备又确确实实会发生老化的现象。因此理解使用指数给设备建模时，一定要记住：在这种情况下，是忽略机器老化的。

在理想情况下，指数分布的无记忆性是指如果随机变量 $X \sim \operatorname{Exp}(\lambda)$ , 则对任意 $s>0, t>0$ , 有

P(X>s+t \mid X>s)=P(X>t) .

上式可以理解为: 记 $X$ 是某种产品的使用寿命 ( $\mathrm{h})$ , 若 $X$ 服从指数分布, 那么已知此产品使用了 $s(\mathrm{~h})$ 没发生故障, 则再能使用 $t(\mathrm{~h})$ 而不发生故障的概率与已使用的 $s(\mathrm{~h})$ 无关, 只相当于重新开始使用 $t(\mathrm{~h})$ 的概率, 即对已使用过的 $s(\mathrm{~h})$ 没有记忆.

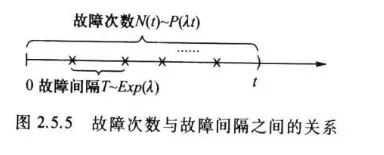
以下例子说明了泊松分布与指数分布的关系. 例 如果某设备在长为 $t$ 的时间 $[0, t]$ 内发生故障的次数 $N(t)$ (与时间长度 $t$ 有关)服从参数为 $\lambda t$ 的泊松分布, 则相继两次故障之间的时间间隔 $T$ 服从参数为 $\lambda$ 的指数分布. 解设 $N(t) \sim P(\lambda t)$ , 即

P(N(t)=k)=\frac{(\lambda t)^k}{k !} \mathrm{e}^{-\lambda t}, \quad k=0,1, \cdots .

注意到两次故障之间的时间间隔 $T$ 是非负随机变量, 且事件 $\{T \geqslant t\}$ 说明此设备在 $[0, t]$ 内没有发生故障, 即 $\{T \geqslant t\}=\{N(t)=0\}$ , 由此我们得当 $t<0$ 时, 有 $F_T(t)=P(T \leqslant t)=0$ ; 当 $t \geqslant 0$ 时, 有

F_T(t)=P(T \leqslant t)=1-P(T>t)=1-P(N(t)=0)=1-\mathrm{e}^{-\lambda t},

所以 $T \sim \operatorname{Exp}(\lambda)$ , 即相继两次故障之间的时间间隔 $T$ 服从参数为 $\lambda$ 的指数分布, 图 2.5 .5 示意其间关系.

$图片$

理解：如何理解无记忆性

上面举的例子说：电子元件在使用过 $a$ 小时后，它还能再使用 $b$ 小时，和它一开始寿命就是 $b$ 小时的概率是一样的。可是这个结果和我们日期生活中的“感觉”相反，这是因为，在数学里，把机器寿命理想化了，即器件不会老化，在这种情况下，我们认为电器的寿命服从指数分布。

如果指数分布不容易理解，可以类比二项分布，二项分布也具有无记性：有一个赌徒在赌大小，他一直在押“大”，可是台上连续出了十把“小”，让他输了很多钱：赌徒认为，前面出了那么多把“小”，再出“小”的可能性非常小了，他想把他的全部身家押“大”，搏一把翻本。这是一个典型的几何分布，前面的分布和后面无关，这就是二项分布无记性的表现。

注：本文部分摘自微信公众号《金朝老师来上课》