26._课外阅读_柯西分布 - 概率论与数理统计

柯西分布

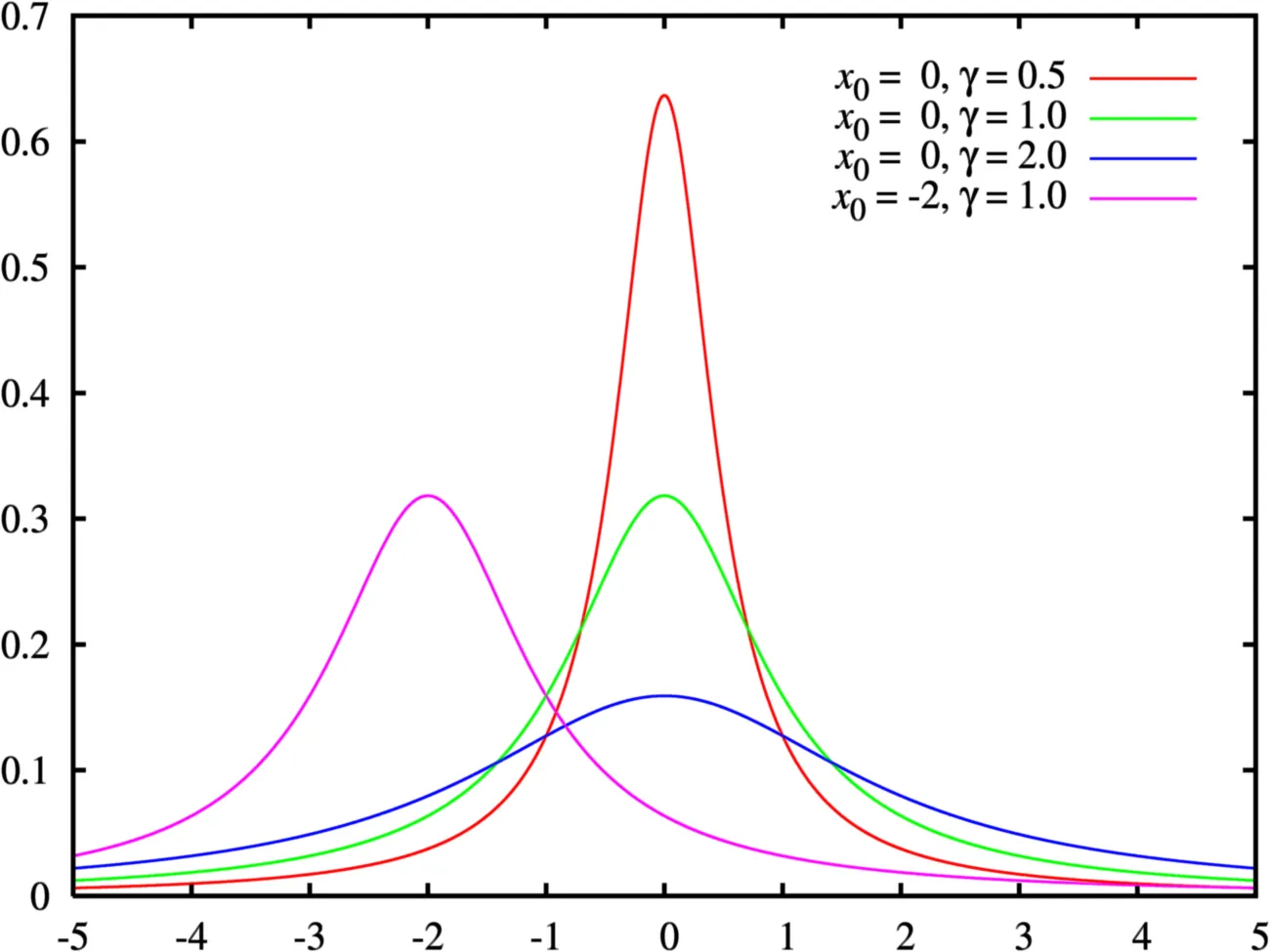
柯西分布也叫作柯西-洛伦兹分布，它是以奥古斯丁·路易·柯西与亨德里克·洛伦兹名字命名的连续概率分布，其概率密度函数为

\begin{aligned} & f\left(x ; x_0, \gamma\right)=\frac{1}{\pi \gamma\left[1+\left(\frac{x-x_0}{\gamma}\right)^2\right]} \\ & =\frac{1}{\pi}\left[\frac{\gamma}{\left(x-x_0\right)^2+\gamma^2}\right] \end{aligned}

其中 $x_0$ 是定义分布峰值位置的位置参数， $y$ 是尺度参数，是半峰全宽／四分位距的一半。

$图片$ {width=400px}

作为概率分布，通常叫作柯西分布，物理学家也将之称为洛伦兹分布或者Breit－Wigner分布。在物理学中的重要性很大—部分归因于它是描述受迫共振的微分方程的解。在光谱学中，它描述了被共振或者其它机制加宽的谱线形状。在下面的部分将使用柯西分布这个统计学术语。

标准柯西分布

$x_0=0$ 且 $y=1$ 的特例称为标准柯西分布，其概率密度函数为

\boxed{ f(x ; 0,1)=\dfrac{1}{\pi\left(1+x^2\right)} }

对 $1 /\left(1+x^2\right)$ 的原函数是 $\arctan (x)$ ，于是

\int_{-\infty}^{\infty} \frac{d x}{1+x^2}=2 \int_0^{\infty} \frac{d x}{1+x^2}=2[\arctan (\infty)-\arctan (0)]=2\left[\frac{\pi}{2}-0\right]= \pi

因此，为了使积分值为 1 ，上式必须要乘以 $1 / \pi$ 。

柯西分布没有数学期望值

柯西分布没有数学期望值，柯西分布为什么没有数学期望值？我们不是应该考察

\int_{-\infty}^{\infty} x \frac{d x}{\pi\left(1+x^2\right)}

吗？奇函数在对称区间上的积分不应该等于 0 吗？与往常一样，出问题的地方与无穷大有关——当涉及无穷大时，你一定要非常小心．正确说法是这样的：这种反常积分存在，当且仅当

\lim _{A, B \rightarrow \infty} \int_{-A}^B x \frac{d x}{\pi\left(1+x^2\right)}

存在，而且无论 $A, B$ 以何种方式趋近于无穷大，上述积分值保持不变。不幸的是，在我们的例子中，积分值与 $A, B$ 趋近于无穷大的方式有关．例如，如果 $B=A$ ，那么积分值是 0 ，但当 $B=2 A$ 时，从 $-A$ 到 $A$ 的积分值为 0 ，这样就得到了

\lim _{A \rightarrow \infty} \int_{-A}^{2 A} x \frac{d x}{\pi\left(1+x^2\right)}=\lim _{A \rightarrow \infty} \int_A^{2 A} \frac{x d x}{\pi\left(1+x^2\right)}

当 $A$ 较大时， $x /\left(1+x^2\right)$ 近似于 $1 / x$ （更精确的说法是， $x /\left(1+x^2\right)$ 大于等于 $1 / 2 x$ ，且小于等于 $1 / x)$ ，那么积分值就近似于

\lim _{A \rightarrow \infty} \int_A^{2 A} \frac{d x}{\pi x}=\frac{1}{\pi}[\log (2 A)-\log (A)]=\frac{\log (2)}{\pi} \neq 0

因此，均值的积分与趋近于无穷大的路径有关，所以均值不存在（请参阅习题 15．10．23）。方差的情况更糟，它显然是无穷大．注意，当 $x \geqslant 2016$ 时，我们有 $x^2 /\left(1+x^2\right) \geqslant$ $1 / 2$ ，从而有

\int_{-\infty}^{\infty} x^2 \frac{d x}{\pi\left(1+x^2\right)} \geqslant \int_{2016}^{\infty} \frac{d x}{2 \pi}=\infty

柯西分布是最重要的分布之一，你必须掌握并记住它。因为服从柯西分布的随机变量没有均值且方差为无穷大，所以其性质与我们研究过的其他随机变量有很大不同．因此，如果想知道一个结果是否适用于所有的概率密度函数，那么用柯西分布或者＂更好＂的分布（比如均匀分布，指数分布，高斯分布……）来验证你的猜想是个不错的选择。

柯西分布在一些经济学理论中起着重要的作用。随机游走假设的一个简单变体断言，股价运动可以通过抛掷相互独立的硬币来很好地模拟，这样就导致了中心极限定理和高斯特性的出现．然而，数据表明，存在比该理论所预测的更大的波动天数，并且需要使用比高斯分布方差更大的分布。事实证明，柯西分布和高斯分布可以放在同一个具有不同参数的族中。有趣的是，两者都是稳定分布