24._离散型随机变量函数的分布

初学者疑惑，已经学了连续型分布了，怎么又有随机变量函数的分布。随机变量函数的分布可以说是对随机变量再次定义随机变量。怎么比喻呢？比如函数$y=f(x)$，对它导数，可以得一阶导数 $y'=f'(x)$ ，如果把一阶导数再次求导，就得到二阶导数$y''=f''(x)$ ，这个二阶导数就可以看成原函数的导数的导数。随机变量函数的分布和此类似，他类似求复合的随机变量。比如我们已经知道随机变量半径为$X$的圆的分布，现在要求面积的，因为面积是$S=\pi X^2$，此时就可以看成是求“$\pi X^2$” 的分布。

离散型随机变量函数的分布

设随机变量 $X$ ，定义一个函数 $g(x)$ ，则 $Y=g(X)$ 是随机变量 $X$ 的函数，也是 一个随机变量。问题: 已知 $X$ 的分布，如何求 $Y=g(X)$ 的分布. 设离散型随机变量 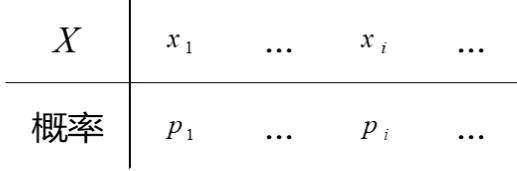$X$ 的分布律为 则 $Y=g(X)$ 的分布律为

但要注意的是，与 $g\left(x_i\right)$ 取相同值对应的那些概率应合并相加。这其实很好理解，比如 产品包装超2g的占比3%，不足2g占比4%，如果求$X^2$的分布，自然要把超过和不足合起来算。 请参见例题

例设随机变量 $X$ 的分布律为 （1）求 $Y=X+2$ 的分布律； （2）求 $W=X^2$ 的分布律。

解：（1）随机变量 $Y=X+2$ 的取值为 $0,1,2,4$ 且 $P(Y=y)=P(X=y-2)$ ． 由此得到相应的分布律：

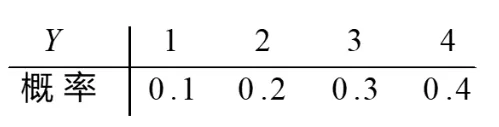
（2） 根据$X$分布表，按照$W=X^2$,在$X$上每个参数都平方，即

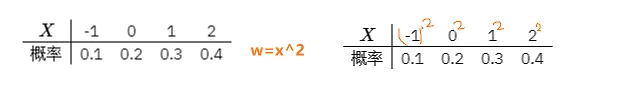
随机变量 $W=X^2$ 的取值为 $0,1,4$ （因为 -1 和 1的平方都是1），

进而可得对应的分布律为：（唯一注意一点 -1 和 1 经过平方后，概率值要合并）

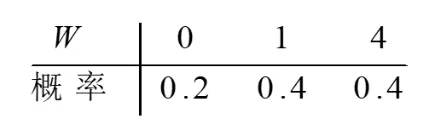
例已知随机变量 $X$ 的分布律如表 2－15 所示．求 $Y=X^2+X$ 的分布律．

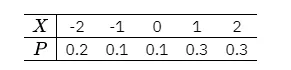
解 $Y=X^2+X$ 的分布律如表 所示．

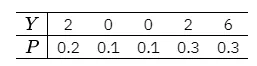
再对相等的值合并，得表