正态检验主要检验μ 和 σ2 他们共有四种情况:
(1) σ2 已知,对 μ 的检验(称做Z检验法或U检验法)
(2) σ2 未知,对 μ 的检验(称做T检验法)
(3) μ 已知,对σ2的检验 (这种情况极少使用)
(4)μ 未知,对σ2的检验(称作χ2 开方检验)
本节介绍均值,下一节介绍方差。
正态检验
由于实际问题中大多数随机变量服从或近似服从正态分布,所以正态检验与正态分布基本上是等价的,且计算分位数或查相应的分布表比较方便。我们把这种利用服从标准正态分布统计量的检验方法称为正态检验。
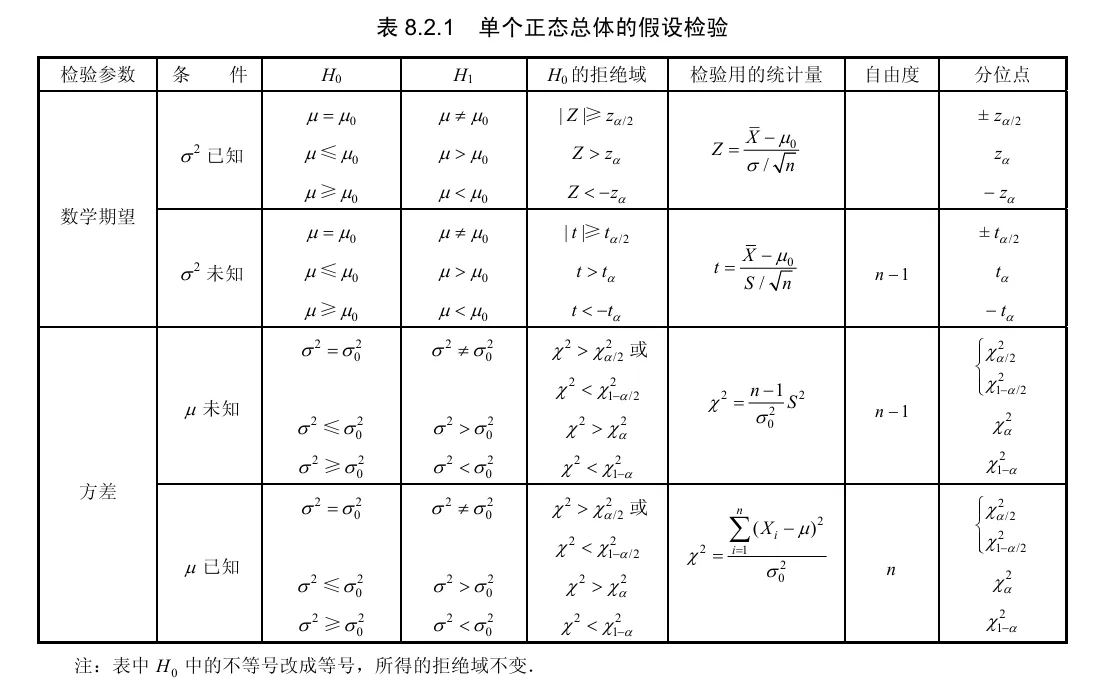
正态检验功能强大,内容繁多下表列出主要公式,并介绍常见的几种检验方法。
双边检验与单边检验
在假设检验中,H0:μ=μ0 ,备择假设 H1:μ=μ0 的意思是 μ 可能大于 μ0 ,也可能小于 μ0 ,称为双边备择假设,并称形如H0:μ=μ0,H1:μ=μ0 的假设检验为双边检验.但有时我们只关心总体均值是否增大,例如,试验新工艺以提高材料的强度,这时所考虑的总体均值应该越大越好,如果我们能判断在新工艺下总体均值较以往正常生产的总体均值大,则可考虑采用新工艺。此时,我们需要检验假设:
H0:μ⩽μ0;H1:μ>μ0....(8.5) 形如(8.5)式的假设检验,称为右边检验。
类似地,有时我们需要检验假设:
H0:μ⩾μ0;H1:μ<μ0...(8.6) 形如(8.6)式的假设检验,称为左边检验.右边检验与左边检验统称为单边检验.
本章内容一定要配合例题来理解
1.σ2 已知,关于 μ 的检验 (U检验或Z检验)
首先考虑以下假设检验.
(1)双侧检验-检验假设
H0:μ=μ0;H1:μ=μ0 ( μ0 为已知常数). 当 H0 为真时,由定理可知
Z=σ/nXˉ−μ0∼N(0,1), 故选取 Z 作为检验统计量,记其观察值为 z ,相应的检验法称为 Z 检验法或 U检验法.
因为 Xˉ 是 μ 的无偏估计量,当 H0 成立时, xˉ 应接近 μ0 ,即 ∣z∣ 不应太大,当 H1 成立时, xˉ 与 μ0 有较大的偏差,即 ∣z∣ 有偏大的趋势,故拒绝域形式为
∣z∣=σ/nxˉ−μ0⩾k(k 待定 ). 对于给定的显著性水平 α ,有
P{∣Z∣⩾zα/2}=α. 如图所示,拒绝域为
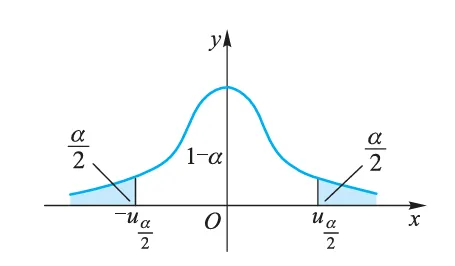
∣z∣=σ/nxˉ−μ0⩾zα/2, 即
W={∣z∣⩾zα/2} 根据一次抽样后得到的样本观察值 x1,x2,⋯,xn 计算出 Z 的观察值 z ,若 ∣z∣⩾zα/2 ,则拒绝原假设 H0 ,即认为总体均值与 μ0 有显著差异;若 ∣z∣<zα/2 ,则接受原假设 H0 ,即认为总体均值与 μ0 无显著差异。
类似地推导,对单侧检验有:
(2)单侧检验-检验假设
H0:μ⩾μ0;H1:μ<μ0 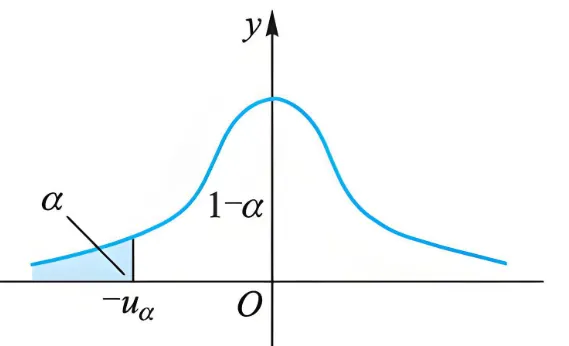 {width=455px}
{width=455px}
对应的拒绝域为
W={z⩽−zα} (3)单侧检验-检验假设
H0:μ⩽μ0;H1:μ>μ0 对应的拒绝域为
W={z⩾zα} 下面的例题对上面进行了解释。
例某车间生产钢丝,用 X 表示钢丝的折断力,由经验判断 X∼N(μ,σ2) ,其中 μ=570,σ2=82 ;今换了一批材料,从性能上看估计折断力的方差 σ2 不会有什么变化(仍有 σ2=82 ),但不知折断力的均值 μ 和原先有无差别。现抽得样本,测得其折断力为
578572570568572570570572596584 取 α=0.05 ,试检验折断力均值有无变化.
解:
题目已经知道了方差,要判断钢丝断裂里的均值μ是否等于570,此时就做两个假设:假设钢丝断裂的力为570和不是570,然后根据断裂力为570构建正态分布,推导看有没有矛盾。
(1)建立假设 H0:μ=μ0=570,H1:μ=570 .
(2)根据正态抽样, 选择统计量 Z=σ/nXˉ−μ0∼N(0,1) .
(3)对于给定的显著性水平 α ,确定 k ,使 P{∣Z∣>k}=α .
显著性水平α,在 枢轴变量 曾经说过,我们总是把α一分为二进行处理,所以左侧阴影面积为 0.025
但是,这个面积直接查找正态分布表里是没有的,根据对称性我们其实是查找的0.975的面积,他对应的值为 1.96,详见 置信区间与上a分位数
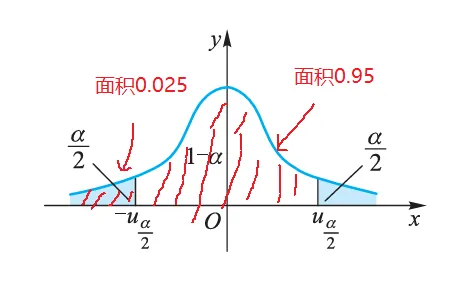
现在切换到正态分布视图,查正态分布表得 k=zα/2=z0.025=1.96 ,从而拒绝域为 ∣z∣>1.96 .
(4)由于 xˉ=101∑i=110xi=575.20,σ2=64 ,所以
∣z∣=σ/nxˉ−μ0=2.06>1.96, 故应拒绝 H0 ,即认为折断力的均值发生了变化.
例 已知某炼铁厂铁水含碳量服从正态分布 N(4.5,0.12) .今年采用一种新工艺,现测定了 9 炉铁水,其平均含碳量为 4.56.若估计方差没有变化,则现在生产的铁水平均含碳量较上年有无显著性变化(显著性水平 α=0.05 )?
解 提出假设:
H0:μ=μ0=4.5;H1:μ=μ0=4.5. 选取统计量 Z=σ/nX−μ0 ,若 H0 为真,则 Z∼N(0,1) 。
一方面,对于 α=0.05 ,查表,得 z2α=z0,025=1.96 .另一方面,计算统计量 Z 的观察值,有
∣z0∣=σ/nxˉ−μ0=0.1/94.56−4.5=1.8<1.96. 由于 ∣z0∣<z2α ,因此,不能拒绝原假设 H0 ,即不能认为铁水平均含碳量较上年有显著性变化.
方差 σ2 末知,关于 μ 的假设检验( T 检验,T-test)
(1)双侧检验-检验假设
H0:μ=μ0;H1:μ=μ0 ( μ0 为已知常数) 由统计分布知,当 H0 为真时,
T=S/nXˉ−μ0∼t(n−1) 故选取 T 作为检验统计量,记其观察值为 t .相应的检验法称为 T 检验法.
由于 Xˉ 是 μ 的无偏估计量,S2 是 σ2 的无偏估计量,当 H0 成立时,∣t∣ 不应太大,当 H1成立时,∣t∣ 有偏大的趋势,故拒绝域形式为
∣t∣=s/nxˉ−μ0⩾k(k 待定 ) 对于给定的显著性水平 α ,有
P{∣T∣⩾tα/2(n−1)}=α 如图所示,拒绝域为
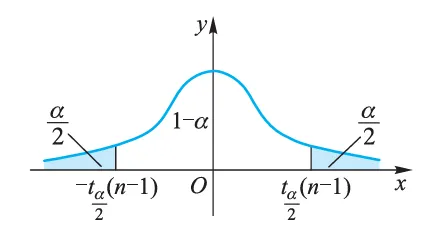
∣t∣=s/nxˉ−μ0⩾tα/2(n−1) 即
W={∣t∣⩾tα/2(n−1)} 根据一次抽样后得到的样本观察值 x1,x2,⋯,xn 计算出 T 的观察值 t ,若 ∣t∣⩾tα/2(n−1) ,则拒绝原假设 H0 ,即认为总体均值与 μ0 有显著差异;若 ∣t∣<tα/2(n−1) ,则接受原假设 H0 ,即认为总体均值与 μ0 无显著差异。
类似地推导,对单侧检验有:
(2)单侧检验-检验假设
H0:μ⩾μ0;H1:μ<μ0 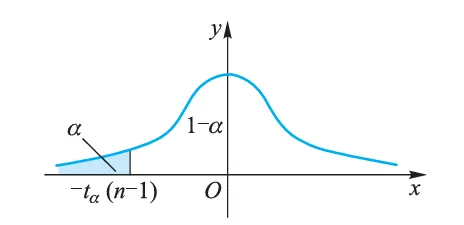
对应的拒绝域为
W={t⩽t1−α(n−1)} ###(3)单侧检验-检验假设
H0:μ⩽μ0;H1:μ>μ0 对应的拒绝域为
W={t⩾tα(n−1)} 例水泥厂用自动包装机包装水泥,每袋额定质量是 50 kg ,某日开工后随机抽查了 9 袋,称得质量如下
49.649.350.150.049.249.949.851.050.2 设每袋质量服从正态分布,问包装机工作是否正常 (α=0.05) ?
解(1)建立假设 H0:μ=50,H1:μ=50 .
(2)选择统计量 T=S/nXˉ−μ0∼t(n−1) .
(3)对于给定的显著性水平 α ,确定 k ,使 P{∣T∣>k}=α .
查附录 D 得 k=tα/2=t0.025(8)=2.306 ,从而拒绝域为 ∣t∣>2.306 .
(4)由于 xˉ=49.9,s2=0.29 ,所以
∣t∣=s/nxˉ−50=0.56<2.306 故应接受H0,即认为包装机工作正常
例设某工厂生产的电灯泡的使用寿命用 X 表示,假定 X 服从正态分布 N(μ,σ2) ,其中 μ 与 σ2 都是未知参数。现抽取 20 个灯泡,测得其使用寿命分别为 x1,x2,⋯,x20 ,并由此算得 xˉ=1880,s=197 。"该厂电灯泡的平均使用寿命为 μ=2000"这一结论是否成立(显著性水平 α=0.05 )?
解 考虑检验假设:
H0:μ=μ0=2000;H1:μ=μ0=2000. 选取统计量
T=S/nXˉ−μ0 当 H0 为真时,T∼t(n−1) .T 的观察值为
∣t0∣=s/nxˉ−μ0=197/201880−2000≈2.72. 对于给定的显著性水平 α=0.05 ,查表,得 t0.025(19)=2.093 .
由于 ∣t0∣≈2.72>t0.025(19) ,因此,应拒绝 H0 即不能认为 μ=2000 .
例题
例 某仪器厂生产的仪表圆盘,其标准直径应为 20( mm) ,在正常情况下,仪表圆盘直径服从正态分布 N(20,1) .为了检查该厂某天生产是否正常,对生产过程中的仪表圆盘随机地抽查了 5 个,测得直径分别为
19,19.5,19,20,20.5, 若显著性水平 α=0.05 ,问:该天生产是否正常?
解 由题意,要检查生产是否正常,实际上就是检验直径均值是否为 20 .
因此,建立假设 H0:μ=20,H1:μ=20 。
当 H0 成立时,检验的统计量
U=nσXˉ−20∼N(0,1). 当显著性水平 α=0.05 时,拒绝域为 ∣U∣>u0.025 ,查正态分布表可得 ∣U∣>1.96 .
由样本值算得 xˉ=19.6 ,代入检验统计量中可得
u=5119.6−20=−0.8944. 因为 ∣u∣<u0.025=1.96 ,这表明统计量的观测值没有落入拒绝域内,故应接受 H0 ,从而认为该天生产的仪表圆盘的直径均值是 20 ,亦即认为该天的生产是正常的.
例葡萄酒中除了水和酒精外,占比最多的就是甘油.甘油是酵母发酵的副产品,它有助于提升葡萄酒的口感和质地,因而经常需要对葡萄酒中的甘油含量进行检测。假设某品牌葡萄酒的甘油含量 X(mg/mL) 服从正态分布,现随机抽查了 5 个样品,测得它们的甘油含量分别为
2.67,4.62,4.14,3.81,3.83 若显著性水平 α=0.05 ,问:是否有理由认为该品牌葡萄酒的平均甘油含量为 4mg/mL ?
解 由题意建立假设 H0:μ=4,H1:μ=4 。
因方差 σ2 未知,故用 T 检验法,检验统计量为
T=nSXˉ−μ0∼t(n−1) 当 α=0.05,n=5 时,拒绝域
∣T∣>t2α(n−1) 为 ∣T∣>t0.025 (4), 即 ∣T∣>2.776. 由样本值算得 xˉ=3.814,s=0.718 ,代入检验统计量中可得
t=0.3213.814−4=−0.58 因为 ∣t∣=0.58<2.776 ,故接受 H0 ,即可以认为该品牌葡萄酒的平均甘油含量为 4mg/mL .
附表

 {width=455px}
{width=455px}


