6.1 Gersgorin 圆盘 如果 A ∈ M n A \in M_{n} A ∈ M n A A A A = D + B A = D + B A = D + B D = diag ( a 11 , ⋯ , a n n ) D = \operatorname{diag}(a_{11}, \cdots, a_{nn}) D = diag ( a 11 , ⋯ , a nn ) A A A B B B ε ∈ C \varepsilon \in C ε ∈ C A ε ≡ D + ε B A_{\varepsilon} \equiv D + \varepsilon B A ε ≡ D + εB A 0 = D A_{0} = D A 0 = D A 1 = A A_{1} = A A 1 = A A 0 = D A_{0} = D A 0 = D a 11 , ⋯ , a n n a_{11}, \cdots, a_{nn} a 11 , ⋯ , a nn ε \varepsilon ε A ε A_{\varepsilon} A ε a 11 , ⋯ , a n n a_{11}, \cdots, a_{nn} a 11 , ⋯ , a nn a i a_{i} a i
6.1.1 定理(Gersgorin) 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n
R i ′ ( A ) ≡ ∑ j = 1 j ≠ i n ∣ a i j ∣ , 1 ⩽ i ⩽ n R _ {i} ^ {\prime} (A) \equiv \sum_ {\substack {j = 1 \\ j \neq i}} ^ {n} | a _ {i j} |, \quad 1 \leqslant i \leqslant n R i ′ ( A ) ≡ j = 1 j = i ∑ n ∣ a ij ∣ , 1 ⩽ i ⩽ n 表示 A A A A A A n n n
⋃ i = 1 n { z ∈ C : ∣ z − a v ∣ ⩽ R i ′ ( A ) } ≡ G ( A ) (6.1.2) \bigcup_ {i = 1} ^ {n} \left\{z \in \mathbf {C}: | z - a _ {v} | \leqslant R _ {i} ^ {\prime} (A) \right\} \equiv G (A) \tag {6.1.2} i = 1 ⋃ n { z ∈ C : ∣ z − a v ∣ ⩽ R i ′ ( A ) } ≡ G ( A ) ( 6.1.2 ) 中.此外,如果这 n \pmb{n} n k \pmb{k} k n − k n - k n − k
都不相交,则在这个区域中恰好有 A A A k k k
证明:设 λ \lambda λ A A A A x = λ x Ax = \lambda x A x = λ x x = [ x i ] ≠ 0 x = [x_{i}] \neq 0 x = [ x i ] = 0 x x x i = 1 , 2 , … , n i = 1, 2, \dots, n i = 1 , 2 , … , n ∣ x p ∣ ⩾ ∣ x i ∣ |x_{p}| \geqslant |x_{i}| ∣ x p ∣ ⩾ ∣ x i ∣ x p ≠ 0 x_{p} \neq 0 x p = 0 A x − λ x Ax - \lambda x A x − λ x
λ r p − [ λ x ] p = [ A x ] p = ∑ i n a p j x j , \lambda r _ {p} - \left[ \lambda x \right] _ {p} = \left[ A x \right] _ {p} = \sum_ {i} ^ {n} a _ {p j} x _ {j}, λ r p − [ λ x ] p = [ A x ] p = i ∑ n a p j x j , 它等价于
344
x p ( λ − a p p ) = ∑ j = 1 j ≠ p n a p j x j x _ {p} (\lambda - a _ {p p}) = \sum_ {\substack {j = 1 \\ j \neq p}} ^ {n} a _ {p j} x _ {j} x p ( λ − a pp ) = j = 1 j = p ∑ n a p j x j 另一方面,三角不等式使我们得出,
∣ x p ∣ ∣ λ − a p p ∣ = ∣ ∑ j = 1 j ≠ p n a p j x j ∣ ⩽ ∑ j = 1 j ≠ p n ∣ a p j x j ∣ = ∑ i = 1 i ≠ p n ∣ a p i ∣ ∣ x j ∣ ⩽ ∣ x p ∣ ∑ j = 1 j ≠ p n ∣ a p j ∣ − − ∣ x p ∣ R p ′ . \begin{array}{l} \left| x _ {p} \right| \left| \lambda - a _ {p p} \right| = \left| \sum_ {\substack {j = 1 \\ j \neq p}} ^ {n} a _ {p j} x _ {j} \right| \leqslant \sum_ {\substack {j = 1 \\ j \neq p}} ^ {n} \left| a _ {p j} x _ {j} \right| = \sum_ {\substack {i = 1 \\ i \neq p}} ^ {n} \left| a _ {p i} \right| \left| x _ {j} \right| \\ \leqslant \left| x _ {p} \right| \sum_ {\substack {j = 1 \\ j \neq p}} ^ {n} \left| a _ {p j} \right| ^ {- - } \left| x _ {p} \right| R _ {p} ^ {\prime}. \\ \end{array} ∣ x p ∣ ∣ λ − a pp ∣ = ∑ j = 1 j = p n a p j x j ⩽ ∑ j = 1 j = p n ∣ a p j x j ∣ = ∑ i = 1 i = p n ∣ a p i ∣ ∣ x j ∣ ⩽ ∣ x p ∣ ∑ j = 1 j = p n ∣ a p j ∣ −− ∣ x p ∣ R p ′ . 因而,对某个 p p p ∣ λ − a p p ∣ ⩽ R p ′ \mid \lambda -a_{pp}\mid \leqslant R_p^{\prime} ∣ λ − a pp ∣ ⩽ R p ′ λ \lambda λ a p p a_{pp} a pp R p ′ R_{p}^{\prime} R p ′ p \pmb{p} p λ \lambda λ λ \lambda λ λ \lambda λ λ \lambda λ
为了证明定理的第二个论断,记 A = D + B A = D + B A = D + B D = diag ( a 11 , ⋯ , a n n ) D = \operatorname{diag}(a_{11}, \cdots, a_{nn}) D = diag ( a 11 , ⋯ , a nn ) A ε ≡ D + ε B A_{\varepsilon} \equiv D + \varepsilon B A ε ≡ D + εB R i ′ ( A i ) = R i ′ ( ε B ) = ε R i ′ ( A ) R_{i}^{\prime}(A_{i}) = R_{i}^{\prime}(\varepsilon B) = \varepsilon R_{i}^{\prime}(A) R i ′ ( A i ) = R i ′ ( εB ) = ε R i ′ ( A ) k k k
⋃ i = 1 k { z ∈ C : ∣ z − a α ∣ ⩽ R i ′ } \bigcup_ {i = 1} ^ {k} \left\{z \in \mathbf {C}: | z - a _ {\alpha} | \leqslant R _ {i} ^ {\prime} \right\} i = 1 ⋃ k { z ∈ C : ∣ z − a α ∣ ⩽ R i ′ } 形成连通区域 G k G_{k} G k n − k n - k n − k G k ′ G_{k}^{\prime} G k ′ G k ′ = G ( A ) ∖ G k G_{k}^{\prime} = G(A) \setminus G_{k} G k ′ = G ( A ) ∖ G k ϵ ∈ [ 0 , 1 ] \epsilon \in [0,1] ϵ ∈ [ 0 , 1 ] A ϵ A_{\epsilon} A ϵ k k k
G k ( ε ) ≡ ⋃ i = 1 k { z ∈ C : ∣ z − a n : ⩽ R r ′ ( A k ) = ε R r ′ ( Λ ) } G _ {k} (\varepsilon) \equiv \bigcup_ {i = 1} ^ {k} \left\{z \in \mathbf {C}: | z - a _ {n} : \leqslant R _ {r} ^ {\prime} (A _ {k}) = \varepsilon R _ {r} ^ {\prime} (\Lambda) \right\} G k ( ε ) ≡ i = 1 ⋃ k { z ∈ C : ∣ z − a n : ⩽ R r ′ ( A k ) = ε R r ′ ( Λ ) } 包含在连通集 G k ≡ G k ( 1 ) G_{k} \equiv G_{k}(1) G k ≡ G k ( 1 ) ε \varepsilon ε G k ( ε ) G_{k}(\varepsilon) G k ( ε ) G k ( ε ) ≡ G n ( ε ) ∖ G k ( ε ) G_{k}(\varepsilon) \equiv G_{n}(\varepsilon) \setminus G_{k}(\varepsilon) G k ( ε ) ≡ G n ( ε ) ∖ G k ( ε ) G k G_{k} G k i = 1 , … , k i = 1, \dots, k i = 1 , … , k λ i ( A 0 ) = a n \lambda_{i}(A_{0}) = a_{n} λ i ( A 0 ) = a n λ i ( A ε ) , ε > 0 \lambda_{i}(A_{\varepsilon}), \varepsilon > 0 λ i ( A ε ) , ε > 0 A A A ε ∈ [ 0 , 1 ] \varepsilon \in [0, 1] ε ∈ [ 0 , 1 ] λ i ( A ε ) ∈ G k ( ε ) ⊂ G k \lambda_{i}(A_{\varepsilon}) \in G_{k}(\varepsilon) \subset G_{k} λ i ( A ε ) ∈ G k ( ε ) ⊂ G k λ i ( A 0 ) \lambda_{i}(A_{0}) λ i ( A 0 ) G k G_{k} G k { λ i ( A ε ) : 0 ⩽ ε ⩽ 1 } \{\lambda_{i}(A_{\varepsilon}): 0 \leqslant \varepsilon \leqslant 1\} { λ i ( A ε ) : 0 ⩽ ε ⩽ 1 } λ i ( A 1 ) = λ i ( A ) \lambda_{i}(A_{1}) = \lambda_{i}(A) λ i ( A 1 ) = λ i ( A ) ε ∈ [ 0 , 1 ] \varepsilon \in [0, 1] ε ∈ [ 0 , 1 ] G k ( ε ) G_{k}(\varepsilon) G k ( ε ) A ε A_{\varepsilon} A ε k k k G k ( ε ) G_{k}(\varepsilon) G k ( ε ) A ε A_{\varepsilon} A ε k k k A 0 A_{0} A 0 n − k n - k n − k G k G_{k} G k G k G_{k} G k G k G_{k} G k G k G_{k} G k
345
(6.1.2)中的区域 G ( A ) G(A) G ( A ) A A A G ( A ) G(A) G ( A ) A A A A ′ A^{\prime} A ′
C j ′ ( A ) ≡ ∑ r − 1 r − j n a i j C _ {j} ^ {\prime} (A) \equiv \sum_ {\substack {r - 1 \\ r - j}} ^ {n} a _ {i j} C j ′ ( A ) ≡ r − 1 r − j ∑ n a ij 描述的且包含 A A A A T A^{\mathrm{T}} A T
6.1.3 推论 如果 A = [ a n ] ∈ M n A = [a_{n}] \in M_{n} A = [ a n ] ∈ M n A A A n n n
⋃ i = 1 n { z ∈ C : ∣ z − a n ∣ ⩽ C r ′ } = G ( A T ) (6.1.4) \bigcup_ {i = 1} ^ {n} \left\{z \in \mathbf {C}: | z - a _ {n} | \leqslant C _ {r} ^ {\prime} \right\} = G \left(A ^ {T}\right) \tag {6.1.4} i = 1 ⋃ n { z ∈ C : ∣ z − a n ∣ ⩽ C r ′ } = G ( A T ) ( 6.1.4 ) 中.此外,如果这些圆盘中的 k k k n − k n - k n − k A A A k k k
练习 证明, A A A G ( A ) ∩ G ( A τ ) G(A) \cap G(A^{\tau}) G ( A ) ∩ G ( A τ ) a i j = i / j a_{ij} = i / j a ij = i / j 3 × 3 3 \times 3 3 × 3 [ a i j ] [a_{ij}] [ a ij ]
因为 A A A A A A G ( A ) G(A) G ( A ) i \pmb{i} i
∣ a n ∣ + R i ′ = ∑ j = 1 n ∣ a y ∣ , \mid a _ {n} \mid + R _ {i} ^ {\prime} = \sum_ {j = 1} ^ {n} \mid a _ {y} \mid , ∣ a n ∣ + R i ′ = j = 1 ∑ n ∣ a y ∣ , 因而这些值的最大者一定是 A A A
6.1.5 推论 如果 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n
ρ ( A ) ⩽ min { max i ∑ j = 1 n ∣ a i j ∣ , max j ∑ i = 1 n ∣ a i j ∣ } . \rho (A) \leqslant \min \left\{\max _ {i} \sum_ {j = 1} ^ {n} | a _ {i j} |, \max _ {j} \sum_ {i = 1} ^ {n} | a _ {i j} | \right\}. ρ ( A ) ⩽ min { i max j = 1 ∑ n ∣ a ij ∣ , j max i = 1 ∑ n ∣ a ij ∣ } . 这个结论是我们意料之中的,因为它是说, ρ ( A ) ⩽ ∥ A ∥ 1 \rho(A) \leqslant \|A\|_1 ρ ( A ) ⩽ ∥ A ∥ 1 ∥ A T ∥ 1 \|A^T\|_1 ∥ A T ∥ 1
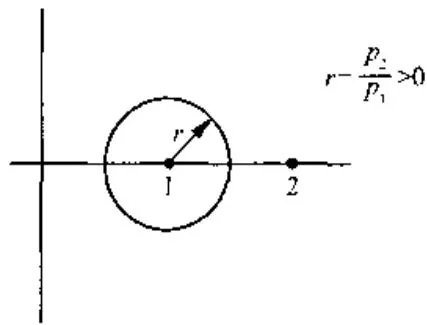
因为只要 S S S S − 1 A S S^{-1}AS S − 1 A S A A A S − 1 A S S^{-1}AS S − 1 A S S S S S = D = d i a g ( p 1 , p 2 , … , p n ) S = D = \mathrm{diag}(p_1, p_2, \dots, p_n) S = D = diag ( p 1 , p 2 , … , p n ) p i > 0 p_i > 0 p i > 0 D − 1 A D = [ p i a i j / p j ] D^{-1}AD = [p_i a_{ij} / p_j] D − 1 A D = [ p i a ij / p j ] D − 1 A D D^{-1}AD D − 1 A D
6.1.6 推论 设 A = [ a n ] ∈ M n A = [a_{n}] \in M_{n} A = [ a n ] ∈ M n p 1 , p 2 , ⋯ , p n p_{1}, p_{2}, \cdots, p_{n} p 1 , p 2 , ⋯ , p n A A A
⋃ i = 1 n { z ∈ C : ∣ z − a i i ∣ ⩽ 1 p i ∑ j = 1 j ≠ i n p j ∣ a i j ∣ } = G ( D − 1 A D ) \bigcup_ {i = 1} ^ {n} \left\{z \in \mathbf {C}: | z - a _ {i i} | \leqslant \frac {1}{p _ {i}} \sum_ {\substack {j = 1 \\ j \neq i}} ^ {n} p _ {j} | a _ {i j} | \right\} = G (D ^ {- 1} A D) i = 1 ⋃ n ⎩ ⎨ ⎧ z ∈ C : ∣ z − a ii ∣ ⩽ p i 1 j = 1 j = i ∑ n p j ∣ a ij ∣ ⎭ ⎬ ⎫ = G ( D − 1 A D ) 中,同时也位于区域
⋃ j = 1 n { z ∈ C : ∣ z − a j ∣ ⩽ p j ∑ i = 1 n 1 p i ∣ a i j ∣ } = G [ ( D − 1 A D ) T ] \bigcup_ {j = 1} ^ {n} \left\{z \in \mathbf {C}: | z - a _ {j} | \leqslant p _ {j} \sum_ {i = 1} ^ {n} \frac {1}{p _ {i}} | a _ {i j} | \right\} = G [ (D ^ {- 1} A D) ^ {T} ] j = 1 ⋃ n { z ∈ C : ∣ z − a j ∣ ⩽ p j i = 1 ∑ n p i 1 ∣ a ij ∣ } = G [( D − 1 A D ) T ] 中.
矩阵 A = [ 1 1 0 2 ] A = \begin{bmatrix} 1 & 1 \\ 0 & 2 \end{bmatrix} A = [ 1 0 1 2 ]
练习 考虑矩阵
A = [ 7 − 16 8 − 16 7 − 8 8 − 8 5 ] . A = \left[ \begin{array}{r r r} 7 & - 1 6 & 8 \\ - 1 6 & 7 & - 8 \\ 8 & - 8 & 5 \end{array} \right]. A = 7 − 16 8 − 16 7 − 8 8 − 8 5 . 试用Gersgorin定理估计一下 A \pmb{A} A A A A D ′ A D D^{\prime}AD D ′ A D D = d i a g ( p 1 , p 2 , p 3 ) D = \mathrm{diag}(p_1,p_2,p_3) D = diag ( p 1 , p 2 , p 3 )
练习 证明, A A A ⋂ D G ( D − 1 A D ) \bigcap_{D} G(D^{-1}AD) ⋂ D G ( D − 1 A D )
我们也可以利用引进自由参数的思想得到关于谐半径估计(6.1.5)的更一般的形式。
6.1.8 推论 设 A = [ a n ] ∈ M n A = [a_{n}] \in M_{n} A = [ a n ] ∈ M n
ρ ( A ) ⩽ min p 1 , … , p n → 0 max 1 ⩽ i ⩽ n 1 p i ∑ j n p j ∣ a j ∣ , \rho (A) \leqslant \min _ {p _ {1}, \dots , p _ {n} \rightarrow 0} \max _ {1 \leqslant i \leqslant n} \frac {1}{p _ {i}} \sum_ {j} ^ {n} p _ {j} | a _ {j} |, ρ ( A ) ⩽ p 1 , … , p n → 0 min 1 ⩽ i ⩽ n max p i 1 j ∑ n p j ∣ a j ∣ , 且
ρ ( A ) ⩽ min p 1 , … , p n … max 1 , … , n p i ∑ i = 1 n 1 p i ∣ a i j ∣ . \rho (A) \leqslant \min _ {p _ {1}, \dots , p _ {n} \dots} \max _ {1, \dots , n} p _ {i} \sum_ {i = 1} ^ {n} \frac {1}{p _ {i}} | a _ {i j} |. ρ ( A ) ⩽ p 1 , … , p n … min 1 , … , n max p i i = 1 ∑ n p i 1 ∣ a ij ∣. 练习 证明推论(6.1.8).
练习 设 A = [ a b c d ] A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} A = [ a c b d ] a , b , c a, b, c a , b , c d d d
(a) 用直接计算求出一个具体的对角矩阵 D ~ \widetilde{D} D ∥ D ~ − 1 A D ∥ = min D ∥ D − 1 A D ∥ \| \widetilde{D}^{-1}AD \| = \min_{D} \| D^{-1}AD\| ∥ D − 1 A D ∥ = min D ∥ D − 1 A D ∥
(b) 计算 ∥ D ~ − 1 Λ D ~ ∥ ∞ = r \|\widetilde{D}^{-1}\Lambda\widetilde{D}\|_{\infty} = r ∥ D − 1 Λ D ∥ ∞ = r
(c) 直接计算 ρ ( A ) \rho(A) ρ ( A )
(d) 指出 r = ρ ( A ) r = \rho(A) r = ρ ( A )
以后将证明,如果 A A A n × n n \times n n × n D ′ A D D^{\prime}AD D ′ A D D D D
练习 考虑 A − [ 1 1 − 1.5 2 ] A - \left[ \begin{array}{rr}1 & 1\\ -1.5 & 2 \end{array} \right] A − [ 1 − 1.5 1 2 ] p 1 p_1 p 1 p 2 p_2 p 2 D = d i a g ( p 1 , p 2 ) D = \mathrm{diag}(p_1, p_2) D = diag ( p 1 , p 2 ) ρ ( A ) < min ∥ D − 1 A D ∥ \rho(A) < \min \| D^{-1}AD\| ρ ( A ) < min ∥ D − 1 A D ∥
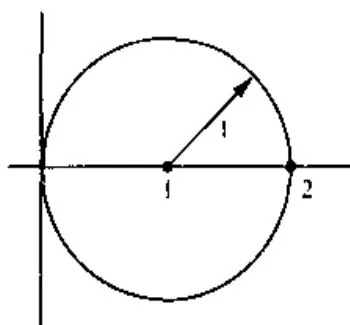
如果有关于一个矩阵的某些附加信息,它要求特征值位于(或不位于)某些集合中,那么,可以利用这个信息以及Gersgorin定理给出特征值的更为准确的估计。例如,如果 A A A A A A R ∩ G ( A ) \mathbb{R} \cap G(A) R ∩ G ( A )
练习 关于斜Hermite矩阵的特征值的估计你能说些什么?关于两矩阵呢?关于实正交矩阵呢?
因为一个矩阵是可逆的当且仅当0不是其特征值,所以,值得研究的是导出从包含特征值的已知区域中去掉原点的条件.
6.1.9 定义 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n A A A
∣ a n ∣ ⩾ ∑ j = 1 n ∣ a n ∣ = R t ′ \mid a _ {n} \mid \geqslant \sum_ {j = 1} ^ {n} \mid a _ {n} \mid = R _ {t} ^ {\prime} ∣ a n ∣ ⩾ j = 1 ∑ n ∣ a n ∣= R t ′ 对所有 i = 1 , … , n i = 1, \dots, n i = 1 , … , n A A A
∣ a n ∣ > ∑ j = 1 n ∣ a n ∣ = R i ′ \mid a _ {n} \mid > \sum_ {j = 1} ^ {n} \mid a _ {n} \mid = R _ {i} ^ {\prime} ∣ a n ∣> j = 1 ∑ n ∣ a n ∣= R i ′ 对所有 i = 1 , … , n i = 1, \dots, n i = 1 , … , n
从位置几何学可知,如果 A A A a n a_{n} a n A A A
6.1.10 定理 设 A − [ a i j ] ∈ M n A - [a_{ij}] \in M_n A − [ a ij ] ∈ M n
(a) A A A
(b)如果 A A A A A A
(c) 如果 A A A A A A A A A
练习 考察 [ 1 1 1 1 ] \left[ \begin{array}{ll}1 & 1\\ 1 & 1 \end{array} \right] [ 1 1 1 1 ] [ 1 1 1 − ε 1 ] \left[ \begin{array}{ll}1 & 1\\ 1 - \varepsilon & 1 \end{array} \right] [ 1 1 − ε 1 1 ]
利用推论(6.1.6)的备用参数,作为可逆性的充分条件的严格对角占优性假设可以稍微放宽一些。
6.1.11 定理 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n A A A i = 1 , … , n i = 1, \dots, n i = 1 , … , n ∣ a n ∣ > R i ′ |a_n| > R_i' ∣ a n ∣ > R i ′ A A A
证明:假设条件是说,对某个 k k k ∣ a k k ∣ = R k ′ \mid a_{kk}\mid = R_k^{\prime} ∣ a kk ∣= R k ′ i ≠ k i\neq k i = k ∣ a n ∣ > R r ′ \mid a_n\mid >R_r' ∣ a n ∣> R r ′
中,对所有 i ≠ k i \neq k i = k p i = 1 p_i = 1 p i = 1 p k = 1 + ε , ε > 0 p_k = 1 + \varepsilon, \varepsilon > 0 p k = 1 + ε , ε > 0 ε > 0 \varepsilon > 0 ε > 0
1 p k ∑ j = 1 j ≠ k n p j ∣ a i j ∣ = 1 1 + ϵ R k ′ < ∣ a k k ∣ , \frac {1}{p _ {k}} \sum_ {\substack {j = 1 \\ j \neq k}} ^ {n} p _ {j} | a _ {i j} | = \frac {1}{1 + \epsilon} R _ {k} ^ {\prime} < | a _ {k k} |, p k 1 j = 1 j = k ∑ n p j ∣ a ij ∣ = 1 + ϵ 1 R k ′ < ∣ a kk ∣ , 且对所有 i ≠ k i \neq k i = k
1 p i ∑ j = 1 j ≠ i n p j ∣ a i j ∣ = R i ′ + ε ∣ a i k ∣ . \frac {1}{p _ {i}} \sum_ {\substack {j = 1 \\ j \neq i}} ^ {n} p _ {j} \mid a _ {i j} \mid = R _ {i} ^ {\prime} + \varepsilon \mid a _ {i k} \mid . p i 1 j = 1 j = i ∑ n p j ∣ a ij ∣= R i ′ + ε ∣ a ik ∣ . 但是,因为 R i ′ < ∣ a k ∣ R_{i}^{\prime} < |a_{k}| R i ′ < ∣ a k ∣ i ≠ k i \neq k i = k ε > 0 \varepsilon > 0 ε > 0 R i ′ + ε ∣ a k ∣ < ∣ a n ∣ R_{i}^{\prime} + \varepsilon |a_{k}| < |a_{n}| R i ′ + ε ∣ a k ∣ < ∣ a n ∣ i ≠ k i \neq k i = k z = 0 z = 0 z = 0 G ( D − 1 A D ) G(D^{-1}AD) G ( D − 1 A D ) A A A
Gersgorin 定理及其各种变形给出了 A A A A A A S − 1 A S S^{-1}AS S − 1 A S A A A
⋂ D G ( D − 1 A D ) , D = d i a g ( p 1 , … , p n ) , 所 有 p i > 0 (6.1.12) \bigcap_ {D} G (D ^ {- 1} A D), \quad D = \mathrm {d i a g} (p _ {1}, \dots , p _ {n}), \quad \text {所 有} p _ {i} > 0 \tag {6.1.12} D ⋂ G ( D − 1 A D ) , D = diag ( p 1 , … , p n ) , 所 有 p i > 0 ( 6.1.12 ) 包含 A ∈ M n A \in M_{n} A ∈ M n
回答是否定的,其理由如下:设 z z z B = [ b i j ] ∈ M n B = [b_{ij}] \in M_n B = [ b ij ] ∈ M n i − 1 , ⋯ , n i - 1, \cdots, n i − 1 , ⋯ , n b n = a n b_n = a_n b n = a n i , j = 1 , ⋯ , n i, j = 1, \cdots, n i , j = 1 , ⋯ , n ∣ b i ∣ = ∣ a j ∣ |b_i| = |a_j| ∣ b i ∣ = ∣ a j ∣ z z z B B B
习题 350
考虑 n × n n \times n n × n A x = y Ax = y A x = y A A A y y y
(i)定义 B ≡ I − A B \equiv I - A B ≡ I − A x = B x + y x = Bx + y x = B x + y
(ii)按你所需要的任一方式选择解的初始逼近 x ( 0 ) x^{(0)} x ( 0 )
(Ⅲ)对 m = 0 , 1 , 2 , … m = 0,1,2,\dots m = 0 , 1 , 2 , … x ( m + 1 ) = B x ( m ) + y . x^{(m + 1)} = Bx^{(m)} + y. x ( m + 1 ) = B x ( m ) + y .
(iv)可以指望,当 m → ∞ m \to \infty m → ∞ x ( m ) → x x^{(m)} \to x x ( m ) → x
(a) 试用 ε ( m ) = x ( m ) − x \varepsilon^{(m)} = x^{(m)} - x ε ( m ) = x ( m ) − x m m m ε ( m ) = B m ( x ( 0 ) − x ) \varepsilon^{(m)} = B^{m}(x^{(0)} - x) ε ( m ) = B m ( x ( 0 ) − x ) ρ ( I − A ) < 1 \rho(I - A) < 1 ρ ( I − A ) < 1 x ( 0 ) x^{(0)} x ( 0 ) m → ∞ m \to \infty m → ∞ x ( m ) → x x^{(m)} \to x x ( m ) → x A A A
证明, ⋂ S G ( S − 1 A S ) = σ ( A ) \bigcap_{S} G(S^{-1}AS) = \sigma(A) ⋂ S G ( S − 1 A S ) = σ ( A ) S S S
利用(6.1.5)证明,对任意 A ∈ M n A \in M_{n} A ∈ M n
∣ det A ∣ ⩽ ∏ i = 1 n ( ∑ j = 1 n ∣ a i j ∣ ) , \mid \det A \mid \leqslant \prod_ {i = 1} ^ {n} \left(\sum_ {j = 1} ^ {n} \mid a _ {i j} \mid\right), ∣ det A ∣ ⩽ i = 1 ∏ n ( j = 1 ∑ n ∣ a ij ∣ ) , 且对列也有类似的不等式。提示:如果 A A A A A A B B B A A A ρ ( B ) ⩽ 1 \rho(B) \leqslant 1 ρ ( B ) ⩽ 1 ∣ det B ∣ ⩽ 1 |\det B| \leqslant 1 ∣ det B ∣ ⩽ 1
∣ det A ∣ ⩽ ∏ i = 1 n ∥ a i ∥ 1 , \mid \det A \mid \leqslant \prod_ {i = 1} ^ {n} \| a _ {i} \| _ {1}, ∣ det A ∣ ⩽ i = 1 ∏ n ∥ a i ∥ 1 , 其中向量 a i a_{i} a i A A A
在正文中,由 Gersgerin 定理 (6.1.1) 导出了定理 (6.1.10a)-Levy-Desplanques 定理。证明,由 (6.1.10) 的 (a) 部分可推出 (6.1.1) 的前一部分 [区域 (6.1.2) 包含 A A A λ I − A \lambda I - A λ I − A
假定 A ∈ M n A \in M_{n} A ∈ M n n n n A A A A ∈ M n A \in M_{n} A ∈ M n n n n A A A
证明,如果 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n i i i k k k ∣ a n ∣ > R i ′ |a_n| > R_i' ∣ a n ∣ > R i ′ k ⩽ rank A k \leqslant \operatorname{rank} A k ⩽ rank A
假定 A ∈ M n A \in M_{n} A ∈ M n ( A 2 = A ) (A^{2} = A) ( A 2 = A ) A ≠ I A \neq I A = I A A A
假定 A ∈ M n A \in M_{n} A ∈ M n ∣ a n ∣ > R i ′ \left|a_{n}\right| > R_{i}^{\prime} ∣ a n ∣ > R i ′ i = 1 , ⋯ , n i = 1, \cdots, n i = 1 , ⋯ , n ∣ a k ∣ > C k ′ \left|a_{k}\right| > C_{k}^{\prime} ∣ a k ∣ > C k ′ k = 1 , ⋯ , n k = 1, \cdots, n k = 1 , ⋯ , n
假定 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n D = d i a g ( a 11 , a 22 , … , a n n ) D = \mathrm{diag}(a_{11}, a_{22}, \dots, a_{nn}) D = diag ( a 11 , a 22 , … , a nn ) D D D ρ ( I − D − 1 A ) < 1 \rho(I - D^{-1}A) < 1 ρ ( I − D − 1 A ) < 1
设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n R i − R i ′ + ∣ a n ∣ R_i - R_i' + |a_n| R i − R i ′ + ∣ a n ∣ A A A i i i
rank A ⩾ ∑ i = 1 n ∣ a i n ∣ R i , \operatorname {r a n k} A \geqslant \sum_ {i = 1} ^ {n} \frac {\left| a _ {i n} \right|}{R _ {i}}, rank A ⩾ i = 1 ∑ n R i ∣ a in ∣ , 其中约定在这个和中 0 / 0 = 0 0 / 0 = 0 0/0 = 0 a n ⩾ 0 a_{n} \geqslant 0 a n ⩾ 0 R i R_{i} R i A A A
rank A ⩾ ∑ i = 1 n a i . \operatorname {r a n k} A \geqslant \sum_ {i = 1} ^ {n} a _ {i}. rank A ⩾ i = 1 ∑ n a i . 证明, ∑ a n = tr A = ∑ λ i ⩽ ∑ ∣ λ i ∣ ⩽ A \sum a_{n} = \operatorname{tr} A = \sum \lambda_{i} \leqslant \sum |\lambda_{i}| \leqslant A ∑ a n = tr A = ∑ λ i ⩽ ∑ ∣ λ i ∣ ⩽ A ⩽ rank A \leqslant \operatorname{rank} A ⩽ rank A
如果 A = [ a i j ] = [ a 1 a 2 ⋯ a n ] ∈ M n A = [a_{ij}] = [a_1 a_2 \cdots a_n] \in M_n A = [ a ij ] = [ a 1 a 2 ⋯ a n ] ∈ M n
rank A ⩾ ∑ i = 1 n ∣ a n ∣ 2 ∥ a i ∥ 2 2 , \operatorname {r a n k} A \geqslant \sum_ {i = 1} ^ {n} \frac {\left| a _ {n} \right| ^ {2}}{\left\| a _ {i} \right\| _ {2} ^ {2}}, rank A ⩾ i = 1 ∑ n ∥ a i ∥ 2 2 ∣ a n ∣ 2 , 其中约定在这个和中 0 / 0 = 0 0 / 0 = 0 0/0 = 0 A A A ∣ a t ∣ 2 = 1 \mid a_{t}\mid_{2} = 1 ∣ a t ∣ 2 = 1
rank A ⩾ ∑ i = 1 n ∣ a i ∣ 2 = ∑ i = 1 n ∣ e i ∗ a i ∣ 2 , \operatorname {r a n k} A \geqslant \sum_ {i = 1} ^ {n} | a _ {i} | ^ {2} = \sum_ {i = 1} ^ {n} | e _ {i} ^ {*} a _ {i} | ^ {2}, rank A ⩾ i = 1 ∑ n ∣ a i ∣ 2 = i = 1 ∑ n ∣ e i ∗ a i ∣ 2 , 其中 { e 1 , e 2 , … , e n } \{e_1, e_2, \dots, e_n\} { e 1 , e 2 , … , e n } C n \mathbf{C}^n C n A A A k k k k k k v 1 , … , v k ∈ C n v_1, \dots, v_k \in \mathbf{C}^n v 1 , … , v k ∈ C n Span { v 1 , … , v k } = Span { a 1 , … , a n } \operatorname{Span}\{v_1, \dots, v_k\} = \operatorname{Span}\{a_1, \dots, a_n\} Span { v 1 , … , v k } = Span { a 1 , … , a n }
a i = ∑ j = 1 k ( v j ∗ a i ) v j , 因 而 e i ∗ a i = ∑ j = 1 k ( v j ∗ a i ) ( e i ∗ v j ) , a _ {i} = \sum_ {j = 1} ^ {k} (v _ {j} ^ {*} a _ {i}) v _ {j}, \quad \text {因 而} \quad e _ {i} ^ {*} a _ {i} = \sum_ {j = 1} ^ {k} (v _ {j} ^ {*} a _ {i}) (e _ {i} ^ {*} v _ {j}), a i = j = 1 ∑ k ( v j ∗ a i ) v j , 因 而 e i ∗ a i = j = 1 ∑ k ( v j ∗ a i ) ( e i ∗ v j ) , 且
∑ i = 1 n ∣ e i ∗ a i ∣ 2 ⩽ ∑ i = 1 n [ ( ∑ j = 1 k ∣ v j ∗ a i ∣ 2 ) ( ∑ j = 1 k ∣ e i ∗ v j ∣ 2 ) ] = ∑ j = 1 k ∑ i = 1 n ∣ e i ∗ v j ∣ 2 = ∑ j = 1 k 1 = k = rank A . \begin{array}{l} \sum_ {i = 1} ^ {n} \left| e _ {i} ^ {*} a _ {i} \right| ^ {2} \leqslant \sum_ {i = 1} ^ {n} \left[ \left(\sum_ {j = 1} ^ {k} \left| v _ {j} ^ {*} a _ {i} \right| ^ {2}\right) \left(\sum_ {j = 1} ^ {k} \left| e _ {i} ^ {*} v _ {j} \right| ^ {2}\right) \right] = \sum_ {j = 1} ^ {k} \sum_ {i = 1} ^ {n} \left| e _ {i} ^ {*} v _ {j} \right| ^ {2} = \sum_ {j = 1} ^ {k} 1 \\ = k = \operatorname {r a n k} A. \\ \end{array} ∑ i = 1 n ∣ e i ∗ a i ∣ 2 ⩽ ∑ i = 1 n [ ( ∑ j = 1 k v j ∗ a i 2 ) ( ∑ j = 1 k ∣ e i ∗ v j ∣ 2 ) ] = ∑ j = 1 k ∑ i = 1 n ∣ e i ∗ v j ∣ 2 = ∑ j = 1 k 1 = k = rank A . 进一步阅读 用数值例子讨论Gersgorin定理可以在[Stc]中找到。原始资料可参看S. Gersgorin, “Uber die Abgrenzung der Eigenwerte einer Matrix,” Izv. Akad. Nauk. S. S. S. R. 7(1931), 749-754. Gersgorin定理有一个推广,它给出了关于广义特征值问题 A x = λ B x Ax = \lambda Bx A x = λ B x B B B
6.2 Gersgorin 圆盘——更细致的讨论 我们已经看到,严格对角占优性对于可逆性是充分的,但对角占优性则不是。某些 2 × 2 2 \times 2 2 × 2
; a n ∣ > ∑ i = 1 n ∣ a n ∣ 对 i = 1 , … , n 中 至 少 一 个 值 成 立 (6.2.1) ; a _ {n} \mid > \sum_ {i = 1} ^ {n} \mid a _ {n} \mid \quad \text {对} i = 1, \dots , n \text {中 至 少 一 个 值 成 立} \tag {6.2.1} ; a n ∣> i = 1 ∑ n ∣ a n ∣ 对 i = 1 , … , n 中 至 少 一 个 值 成 立 ( 6.2.1 ) 可能是可逆性的充分条件。令人失望的是,正如例子
[ 4 2 1 0 1 1 0 1 1 ] (6.2.2) \left[ \begin{array}{l l l} 4 & 2 & 1 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array} \right] \tag {6.2.2} 4 0 0 2 1 1 1 1 1 ( 6.2.2 ) 所说明的那样,情况并非如此。这里究竟会出现什么情形呢?
但是,关于对角占优矩阵,存在一些普通条件,在这些条件下,(6.2.1)足以保证可逆性,并且它们在图论中诱导出一些很有意义的想法。一个重要论断是,如果 A A A
练习 证明,如果一个给定点 λ \lambda λ A A A
∣ λ − a n ∣ ⩾ R i ′ = ∑ j = 1 n ∣ a i j ∣ (6.2.2a) \mid \lambda - a _ {n} \mid \geqslant R _ {i} ^ {\prime} = \sum_ {j = 1} ^ {n} \mid a _ {i j} \mid \tag {6.2.2a} ∣ λ − a n ∣ ⩾ R i ′ = j = 1 ∑ n ∣ a ij ∣ ( 6.2.2a ) 对所有 i = 1 , ⋯ , n i = 1, \cdots, n i = 1 , ⋯ , n G ( A ) G(A) G ( A ) λ \lambda λ λ = 0 \lambda = 0 λ = 0 A = [ 1 1 1 i ] ⊕ [ − 1 1 1 − i ] A = \left[ \begin{array}{cc}1 & 1 \\ 1 & i\end{array} \right] \oplus \left[ \begin{array}{cc}-1 & 1 \\ 1 & -i\end{array} \right] A = [ 1 1 1 i ] ⊕ [ − 1 1 1 − i ] G ( A ) G(A) G ( A )
仔细分析定理(6.1.1)的证明,当 A A A
6.2.3 引理 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n λ \lambda λ A A A G ( A ) G(A) G ( A ) A x = λ x Ax = \lambda x A x = λ x x = [ x t ] ≠ 0 x = [x_t] \neq 0 x = [ x t ] = 0 p p p ∣ x p ∣ = max 1 ≤ i < j ≤ n ∣ x i ∣ = ∥ x ∥ n ≠ 0 |x_p| = \max_{1 \leq i < j \leq n} |x_i| = \|x\|_n \neq 0 ∣ x p ∣ = max 1 ≤ i < j ≤ n ∣ x i ∣ = ∥ x ∥ n = 0
(a) 如果 k k k ∣ x k ∣ = ∣ x p ∣ \left|x_{k}\right| = \left|x_{p}\right| ∣ x k ∣ = ∣ x p ∣ ∣ λ − a k k ∣ = R k ′ \left|\lambda - a_{kk}\right| = R_{k}^{\prime} ∣ λ − a kk ∣ = R k ′ k k k λ \lambda λ k = 1 , … , n k = 1,\dots ,n k = 1 , … , n ∣ x k ∣ = ∣ x p ∣ \mid x_{k}\mid = \mid x_{p}\mid ∣ x k ∣=∣ x p ∣ j ≠ k j\neq k j = k a k j ≠ 0 a_{kj}\neq 0 a kj = 0
∣ x j ∣ = ∣ x p ∣ . \mid x _ {j} \mid = \mid x _ {p} \mid . ∣ x j ∣=∣ x p ∣ . 证明:正如在Gersgorin定理的证明中所证明的,有
( λ − a u ) x i = ∑ j = 1 j ≠ i n a i j x j (\lambda - a _ {u}) x _ {i} = \sum_ {\substack {j = 1 \\ j \neq i}} ^ {n} a _ {i j} x _ {j} ( λ − a u ) x i = j = 1 j = i ∑ n a ij x j 对所有 i = 1 , … , n i = 1, \dots, n i = 1 , … , n
∣ λ − a n ∣ ∣ x 1 = ∣ ∑ j = 1 n a i j x j ∣ ⩽ ∑ j = 1 n ∣ a i j x j ∣ = ∑ j = 1 n ∣ a i j ∣ ∣ x j ∣ ⩽ ∑ i = 1 n ∣ a i j ∣ ∣ x p ∣ = R i ′ ∣ x p ∣ . (6.2.4) \begin{array}{l} \left| \lambda - a _ {n} \right| | x _ {1} = \left| \sum_ {j = 1} ^ {n} a _ {i j} x _ {j} \right| \leqslant \sum_ {j = 1} ^ {n} | a _ {i j} x _ {j} | = \sum_ {j = 1} ^ {n} | a _ {i j} | | x _ {j} | \\ \leqslant \sum_ {i = 1} ^ {n} | a _ {i j} | | x _ {p} | = R _ {i} ^ {\prime} | x _ {p} |. \tag {6.2.4} \\ \end{array} ∣ λ − a n ∣ ∣ x 1 = ∑ j = 1 n a ij x j ⩽ ∑ j = 1 n ∣ a ij x j ∣ = ∑ j = 1 n ∣ a ij ∣∣ x j ∣ ⩽ ∑ i = 1 n ∣ a ij ∣∣ x p ∣ = R i ′ ∣ x p ∣. ( 6.2.4 ) 因此,如果 k k k ∣ x k ∣ = ∣ x p ∣ \left|x_{k}\right| = \left|x_{p}\right| ∣ x k ∣ = ∣ x p ∣ ∣ λ − a k k ∣ ⩽ R k ′ \left|\lambda - a_{kk}\right| \leqslant R_{k}^{\prime} ∣ λ − a kk ∣ ⩽ R k ′ i = 1 , ⋯ , n i = 1, \cdots, n i = 1 , ⋯ , n ∣ λ − a n ∣ ⩾ R n ′ \left|\lambda - a_{n}\right| \geqslant R_{n}^{\prime} ∣ λ − a n ∣ ⩾ R n ′ i = k i = k i = k
∣ λ − a k k ∣ ∣ x k ∣ = ∑ j = 1 j ≠ k n ∣ a k j ∣ ∣ x j ∣ = ∑ j = 1 j ≠ k n ∣ a k j ∣ ∣ x k ∣ = R k ′ ∣ x k ∣ . \mid \lambda - a _ {k k} \mid \mid x _ {k} \mid = \sum_ {\substack {j = 1 \\ j \neq k}} ^ {n} \mid a _ {k j} \mid \mid x _ {j} \mid = \sum_ {\substack {j = 1 \\ j \neq k}} ^ {n} \mid a _ {k j} \mid \mid x _ {k} \mid = R _ {k} ^ {\prime} \mid x _ {k} \mid . ∣ λ − a kk ∣∣ x k ∣= j = 1 j = k ∑ n ∣ a kj ∣∣ x j ∣= j = 1 j = k ∑ n ∣ a kj ∣∣ x k ∣= R k ′ ∣ x k ∣ . 因为 ∣ x k ∣ = ∥ x ∥ ∞ > 0 |x_k| = \| x\|_{\infty} > 0 ∣ x k ∣ = ∥ x ∥ ∞ > 0
∣ λ − a k k ∣ ∣ x k ∣ = R k ′ ∣ x k ∣ \left| \lambda - a _ {k k} \right| \left| x _ {k} \right| = R _ {k} ^ {\prime} \left| x _ {k} \right| ∣ λ − a kk ∣ ∣ x k ∣ = R k ′ ∣ x k ∣ 推出. 论断(b)可从(f)中的中间恒等式
∑ j = 1 j ≠ k n ∣ a k j ∣ ( ∣ x k ∣ − ∣ x j ∣ ) = 0 \sum_ {j = 1 \atop j \neq k} ^ {n} | a _ {k j} | (| x _ {k} | - | x _ {j} |) = 0 j = k j = 1 ∑ n ∣ a kj ∣ ( ∣ x k ∣ − ∣ x j ∣ ) = 0 推出,因为在这个和中每一项必是非负的。
□
这个引理看起来更偏重于技巧,但是它有下述有用的结果及其推论作为直接推论。
6.2.5 定理 设 A ∈ M n A \in M_{n} A ∈ M n λ \lambda λ A A A λ \lambda λ G ( A ) G(A) G ( A ) λ \lambda λ A A A
(a) A A A λ \lambda λ A x = λ x Ax = \lambda x A x = λ x x = [ x i ] ≠ 0 x = [x_{i}] \neq 0 x = [ x i ] = 0 i i i j = 1 , … , n j = 1, \dots, n j = 1 , … , n ∣ x i ∣ = ∣ x j ∣ |x_{i}| = |x_{j}| ∣ x i ∣ = ∣ x j ∣
练习 从引理(6.2.3)推导定理(6.2.5).
6.2.6 推论 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n A A A A A A i = 1 , … , n i = 1, \dots, n i = 1 , … , n ∣ a i i ∣ > R i ′ |a_{ii}| > R_i' ∣ a ii ∣ > R i ′ A A A
证明:假如 A A A A A A A A A G ( A ) G(A) G ( A ) ∣ a n ∣ > R 1 ′ \left|a_{n}\right| > R_{1}^{\prime} ∣ a n ∣ > R 1 ′ i i i
前一个结果既实用,也有意义,不过,如果利用引理(6.2.3)中更细致的结果,还可以得到更好的结论(不涉及 A A A
6.2.7 定义 我们称矩阵 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n 1 ⩽ p , q ⩽ n 1 \leqslant p, q \leqslant n 1 ⩽ p , q ⩽ n p , q p, q p , q k 1 = p , k 2 , k 3 , … , k m − 1 , k m = q , 1 ⩽ m ⩽ n k_1 = p, k_2, k_3, \dots, k_{m-1}, k_m = q, 1 \leqslant m \leqslant n k 1 = p , k 2 , k 3 , … , k m − 1 , k m = q , 1 ⩽ m ⩽ n
354
有矩阵元素 a k 1 k n , a k n k 3 , … , a k m … k m a_{k_1k_n}, a_{k_nk_3}, \dots, a_{k_m\dots k_m} a k 1 k n , a k n k 3 , … , a k m … k m
例如,矩阵(6.2.2)不具有性质 S C SC SC
利用这个概念和引理(6.2.3),可以得到关于(6.2.5)的下述改进
6.2.8 较好定理 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n λ \lambda λ A A A λ \lambda λ G ( A ) G(A) G ( A ) λ \lambda λ A A A
(a) 每个 Gersgorin 圆经过 λ \lambda λ A x = λ x A x = \lambda x A x = λ x x = [ x i ] ≠ 0 x = [x_{i}] \neq 0 x = [ x i ] = 0 i , j = 1 , … , n i, j = 1, \dots, n i , j = 1 , … , n ∣ x i ∣ = ∣ x j ∣ |x_{i}| = |x_{j}| ∣ x i ∣ = ∣ x j ∣
证明:设 A x = λ x Ax = \lambda x A x = λ x i = 1 , … , n i = 1, \dots, n i = 1 , … , n ∣ x i ∣ ⩽ ∣ x p ∣ = ∥ x ′ ∥ 2 > 0 |x_i| \leqslant |x_p| = \|x'\|^2 > 0 ∣ x i ∣ ⩽ ∣ x p ∣ = ∥ x ′ ∥ 2 > 0 ∣ λ − a p p ′ ∣ = R p ′ |\lambda - a_{pp'}| = R_p' ∣ λ − a p p ′ ∣ = R p ′ q q q 1 ⩽ q ⩽ n 1 \leqslant q \leqslant n 1 ⩽ q ⩽ n q ≠ p q \neq p q = p A A A k 1 = p k_1 = p k 1 = p k 2 = k 3 k_2 = k_3 k 2 = k 3 … \dots … k m = q k_m = q k m = q a k 1 k 2 a_{k_1k_2} a k 1 k 2 … \dots … a k m − 1 k m a_{k_m-1k_m} a k m − 1 k m a k 1 k 2 = a p , q ≠ 0 a_{k_1k_2} = a_{p,q} \neq 0 a k 1 k 2 = a p , q = 0 ∣ x p ∣ = ∣ x k 2 ∣ |x_p| = |x_{k_2}| ∣ x p ∣ = ∣ x k 2 ∣ a k 2 k 1 ≠ 0 a_{k_2k_1} \neq 0 a k 2 k 1 = 0 ∣ x k 3 ∣ = ∣ x k 2 ∣ = ∣ x p ∣ |x_{k_3}| = |x_{k_2}| = |x_p| ∣ x k 3 ∣ = ∣ x k 2 ∣ = ∣ x p ∣ i = 1 , … , m i = 1, \dots, m i = 1 , … , m ∣ x k ∣ = ∣ x p ∣ |x_k| = |x_p| ∣ x k ∣ = ∣ x p ∣ ∣ λ − a k m k m ∣ = ∣ λ − a q i ∣ = R q ′ |\lambda - a_{k_m k_m}| = |\lambda - a_{q_i}| = R_q' ∣ λ − a k m k m ∣ = ∣ λ − a q i ∣ = R q ′ q q q λ \lambda λ ∣ x q ∣ = ∣ x p ∣ |x_q| = |x_p| ∣ x q ∣ = ∣ x p ∣ q q q λ \lambda λ ∣ x i ∣ = ∣ x p ∣ |x_i| = |x_p| ∣ x i ∣ = ∣ x p ∣ i = 1 , … , n i = 1, \dots, n i = 1 , … , n
如同(6.2.6)中那样,从这个结果可以推导出一个关于可逆性的有用充分条件。
6.2.9 较好推论 设 A = [ a n ] ∈ M n A = [a_{n}] \in M_{n} A = [ a n ] ∈ M n A A A Λ \Lambda Λ i = 1 , … , n i = 1, \dots, n i = 1 , … , n ∣ a n ∣ > R i ′ |a_{n}| > R_{i}^{\prime} ∣ a n ∣ > R i ′ Λ \Lambda Λ
练习 由(6.2.8)推导(6.2.9).
练习 证明矩阵(6.2.2)不具有性质SC.
这个陌生的性质SC指的是什么?注意到,它只涉及 A A A A A A
6.2.10 定义 如果 A = [ a i j ] ∈ M m , n A = [a_{ij}] \in M_{m,n} A = [ a ij ] ∈ M m , n ∣ A ∣ = [ ∣ a i j ∣ ] |A| = [|a_{ij}|] ∣ A ∣ = [ ∣ a ij ∣ ] M ( A ) = [ μ i j ] M(A) = [\mu_{ij}] M ( A ) = [ μ ij ] a i j ≠ 0 a_{ij} \neq 0 a ij = 0 μ i j = 1 \mu_{ij} = 1 μ ij = 1 a i j = 0 a_{ij} = 0 a ij = 0 μ i j = 0 \mu_{ij} = 0 μ ij = 0 M ( A ) M(A) M ( A ) A A A
356
练习 证明,矩阵 A ∈ M n A \in M_{n} A ∈ M n ∣ A ∣ |A| ∣ A ∣ M ( A ) M(A) M ( A )
在叙述性质 S C SC SC A A A A A A
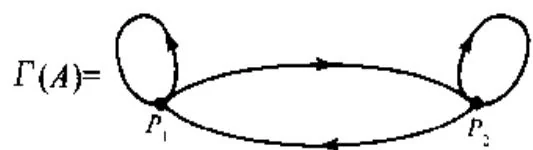
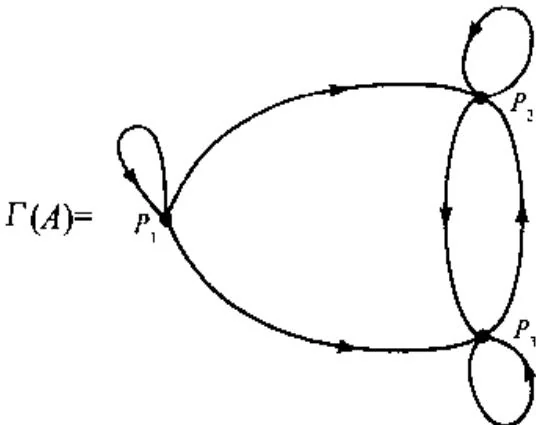
6.2.11 定义 A ∈ M n A \in M_{n} A ∈ M n Γ ( A ) \Gamma(A) Γ ( A ) n n n P 1 , P 2 , ⋯ , P n P_{1}, P_{2}, \cdots, P_{n} P 1 , P 2 , ⋯ , P n Γ ( A ) \Gamma(A) Γ ( A ) P i P_{i} P i P j P_{j} P j a i j ≠ 0 ( μ i j ≠ 0 ) a_{ij} \neq 0 (\mu_{ij} \neq 0) a ij = 0 ( μ ij = 0 )
例
A = [ 1 1 1 1 ] ; A = \left[ \begin{array}{l l} 1 & 1 \\ 1 & 1 \end{array} \right]; A = [ 1 1 1 1 ] ;
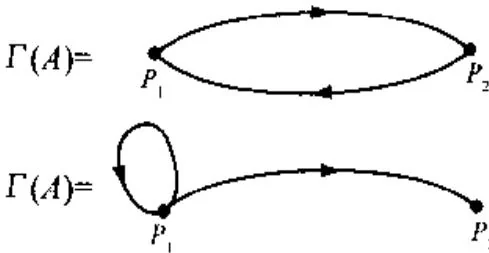
A = [ 0 1 1 0 ] ; A = \left[ \begin{array}{l l} 0 & 1 \\ 1 & 0 \end{array} \right]; A = [ 0 1 1 0 ] ;
A = [ 1 1 0 0 ] ; A = \left[ \begin{array}{c c} 1 & 1 \\ 0 & 0 \end{array} \right]; A = [ 1 0 1 0 ] ; A = [ 4 2 1 0 1 1 0 1 1 ] ; A = \left[ \begin{array}{l l l} 4 & 2 & 1 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array} \right]; A = 4 0 0 2 1 1 1 1 1 ;
6.2.12 定义 图 Γ \Gamma Γ γ \gamma γ Γ \Gamma Γ P t 1 P t 2 P_{t_1}P_{t_2} P t 1 P t 2 P t 2 P t 3 P_{t_2}P_{t_3} P t 2 P t 3 P t 3 P t 1 P_{t_3}P_{t_1} P t 3 P t 1 γ \gamma γ P t 1 P_{t_1} P t 1 P t 2 P_{t_2} P t 2 Γ \Gamma Γ Γ \Gamma Γ P i P_{i} P i P j P_{j} P j P i P_{i} P i P j P_{j} P j A ∈ M A \in M A ∈ M A A A Γ ( A ) \Gamma(A) Γ ( A )
练习 证明定理6.2.14.
练习 证明如果 Γ \Gamma Γ Γ \Gamma Γ
[ 0 1 0 1 0 1 0 1 0 ] . \left[ \begin{array}{l l l} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array} \right]. 0 1 0 1 0 1 0 1 0 . 在有向图的两个结点之间,可能存在多条有向道路,但是具有不同长度的这样两条道路可能没有本质的差别;它们可能包含一条或多条重复出现的子道路。显然,如果我们沿着一条有向道路前进时,曾两次遇到某个结点,那么去掉第一次遇到该结点到第二次遇到该结点间的所有中间弧(去掉的子图是一条回路或包含一条回路),这条有向道路便可以缩短(且两个端点不受影响)。
6.2.15 论断 设 Γ \Gamma Γ n n n Γ \Gamma Γ n − 1 n - 1 n − 1
我们应该怎样说明给定的矩阵 A A A Γ ( A ) \Gamma(A) Γ ( A )
的。如果 n n n M ( A ) M(A) M ( A ) Γ ( A ) \Gamma(A) Γ ( A )
6.2.16 定理 设 A ∈ M n A \in M_{n} A ∈ M n P i P_{i} P i P j P_{j} P j Γ ( A ) \Gamma(A) Γ ( A ) P i P_{i} P i P j P_{j} P j Γ ( A ) \Gamma(A) Γ ( A ) m m m ( ∣ A ∣ m ) i j ≠ 0 (|A|^{m})_{ij} \neq 0 ( ∣ A ∣ m ) ij = 0 [ M ( A ) m ] i j ≠ 0 [M(A)^{m}]_{ij} \neq 0 [ M ( A ) m ] ij = 0
证明:我们用归纳法证明.对 m = 1 m = 1 m = 1 m − 2 m - 2 m − 2
[ ∣ A 12 ] j = ∑ k = 1 n [ ∣ A ∣ ] i k [ ∣ A ∣ ] k j = ∑ k = 1 n ∣ a k ∣ ∣ a k j ∣ , [ \mid A ^ {1 2} ] _ {j} = \sum_ {k = 1} ^ {n} [ \mid A \mid ] _ {i k} [ \mid A \mid ] _ {k j} = \sum_ {k = 1} ^ {n} \left| a _ {k} \right| \left| a _ {k j} \right|, [ ∣ A 12 ] j = k = 1 ∑ n [ ∣ A ∣ ] ik [ ∣ A ∣ ] kj = k = 1 ∑ n ∣ a k ∣ ∣ a kj ∣ , 因而, [ ∣ A ∣ 2 ] i j ≠ 0 [|A|^2]_ij \neq 0 [ ∣ A ∣ 2 ] i j = 0 k k k a i k a_{ik} a ik a k j a_{kj} a kj Γ ( A ) \Gamma(A) Γ ( A ) P i P_i P i P j P_j P j m = q m = q m = q
[ ∣ A ∣ q + 1 ] i j = ∑ k = 1 n [ ∣ A ∣ q ] i k [ ∣ A i ] k j = ∑ k = 1 n [ ∣ A ∣ q ] i k ∣ a k i ∣ ≠ 0 [ | A | ^ {q + 1} ] _ {i j} = \sum_ {k = 1} ^ {n} [ | A | ^ {q} ] _ {i k} [ | A _ {i} ] _ {k j} = \sum_ {k = 1} ^ {n} [ | A | ^ {q} ] _ {i k} | a _ {k i} | \neq 0 [ ∣ A ∣ q + 1 ] ij = k = 1 ∑ n [ ∣ A ∣ q ] ik [ ∣ A i ] kj = k = 1 ∑ n [ ∣ A ∣ q ] ik ∣ a ki ∣ = 0 当且仅当对 k k k [ ∣ A ∣ q ] ∗ \left[ \mid A \mid^q \right]_* [ ∣ A ∣ q ] ∗ ∣ a k j ∣ \left| a_{kj} \right| ∣ a kj ∣ P i P_i P i P k P_k P k q q q P k P_k P k P j P_j P j P i P_i P i P j P_j P j q + 1 q + 1 q + 1 M ( A ) M(A) M ( A )
6.2.17 定义 设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n A ⩾ 0 A \geqslant 0 A ⩾ 0 A A A a i j a_{ij} a ij A > 0 A > 0 A > 0 A A A a i j a_{ij} a ij A ∈ M n A \in M_{n} A ∈ M n ∣ A ∣ m > 0 |A|^{m} > 0 ∣ A ∣ m > 0 Γ ( A ) \Gamma(A) Γ ( A ) P i P_{i} P i P j P_{j} P j Γ ( A ) \Gamma(A) Γ ( A ) m m m M ( A ) m M(A)^{m} M ( A ) m A ∈ M n A \in M_{n} A ∈ M n A A A ( I + ∣ A ∣ ) n − 1 > 0 (I + |A|)^{n-1} > 0 ( I + ∣ A ∣ ) n − 1 > 0 [ I + M ( A ) ] n − 1 > 0 [I + M(A)]^{n-1} > 0 [ I + M ( A ) ] n − 1 > 0
证明: ( I + ∣ A ∣ ) n − 1 = I + ( n − 1 ) ∣ A ∣ + ( n − 1 2 ) ∣ A ∣ 2 + ⋯ + ( n − 1 n − 2 ) ∣ A ∣ n − 1 > 0 (I + |A|)^{n - 1} = I + (n - 1) |A| + \binom{n - 1}{2} |A|^2 + \cdots + \binom{n - 1}{n - 2} |A|^{n - 1} > 0 ( I + ∣ A ∣ ) n − 1 = I + ( n − 1 ) ∣ A ∣ + ( 2 n − 1 ) ∣ A ∣ 2 + ⋯ + ( n − 2 n − 1 ) ∣ A ∣ n − 1 > 0 ( i , j ) (i, j) ( i , j ) i ≠ j i \neq j i = j ∣ A ∣ |A| ∣ A ∣ ∣ A ∣ 2 |A|^2 ∣ A ∣ 2 ∣ A ∣ n − 1 |A|^{n - 1} ∣ A ∣ n − 1 ( i , j ) (i, j) ( i , j ) Γ ( A ) \Gamma(A) Γ ( A ) P i P_i P i P j P_j P j Γ ( A ) \Gamma(A) Γ ( A ) A A A
练习 证明推论(6.2.19)中涉及 M ( A ) M(A) M ( A )
6.2.20推论在 Γ ( A ) \Gamma (A) Γ ( A ) P i P_{i} P i P j P_{j} P j [ I + ∣ a ∣ ) n − 1 ] i j ≠ 0. [I + |a|)^{n - 1}]_{ij}\neq 0. [ I + ∣ a ∣ ) n − 1 ] ij = 0.
练习 试用推论(6.2.19)给出关于性质 S C SC SC log 2 ( n − 1 ) \log_2(n - 1) log 2 ( n − 1 ) n − 2 n - 2 n − 2 ( I + ∣ A ∣ ) 2 (I + |A|)^2 ( I + ∣ A ∣ ) 2
在结束这个论题以前,我们要引进性质SC的另外一个等价的描述。它基于 Γ ( A ) \Gamma(A) Γ ( A ) Γ ( A ) \Gamma(A) Γ ( A ) Γ ( A ) \Gamma(A) Γ ( A ) A A A i i i j j j i i i j j j Γ ( A ) \Gamma(A) Γ ( A ) P i P_{i} P i P j P_{j} P j
一样.
我们知道,转置矩阵 P P P A A A P T = P − 1 P^{\mathrm{T}} = P^{-1} P T = P − 1 P P P i , j i, j i , j p i i = p j j = 1 p_{ii} = p_{jj} = 1 p ii = p jj = 1 P T A P P^{\mathrm{T}}AP P T A P A A A A A A i i i j j j A A A i i i j j j A A A P P P A A A A A A P T A P P^{\mathrm{T}}AP P T A P A A A A A A
6.2.21 定义 矩阵 A A A
(a) n = 1 n = 1 n = 1 A = 0 A = 0 A = 0
(b) n ⩾ 2 n \geqslant 2 n ⩾ 2 P ∈ M n P \in M_{n} P ∈ M n 1 ⩽ r ⩽ n − 1 1 \leqslant r \leqslant n - 1 1 ⩽ r ⩽ n − 1 r r r
P T A P = [ B C 0 D ] , P ^ {T} A P = \left[ \begin{array}{c c} B & C \\ 0 & D \end{array} \right], P T A P = [ B 0 C D ] , 其中, B ∈ M r B\in M_r B ∈ M r D ∈ M n − r D\in M_{n - r} D ∈ M n − r C ∈ M r , n − r C\in M_{r,n - r} C ∈ M r , n − r 0 ∈ M n − r 0\in M_{n - r} 0 ∈ M n − r
注意,我们并没要求子块 B B B C C C D D D ( n − r ) × r (n - r)\times r ( n − r ) × r ∣ A ∣ > 0 \mid A\mid >0 ∣ A ∣> 0 A A A A A A ( n − 1 ) (n - 1) ( n − 1 )
附注假如想解线性方程组 A x = y Ax = y A x = y A A A A ~ = P T A P = [ B C 0 D ] \widetilde{A} = P^T A P = \left[ \begin{array}{cc}B & C\\ 0 & D \end{array} \right] A = P T A P = [ B 0 C D ] Λ x = P A ~ P T x = y \Lambda x = P\widetilde{A} P^{T}x = y Λ x = P A P T x = y A ~ ( P T x ) = P T y \widetilde{A} (P^T x) = P^T y A ( P T x ) = P T y P T x = x ^ = [ z T : ζ T ] T P^T x = \widehat{x} = [z^T:\zeta^T ]^T P T x = x = [ z T : ζ T ] T P T y = y ˉ = [ w T : ω T ] T P^T y = \bar{y} = [w^T:\omega^T ]^T P T y = y ˉ = [ w T : ω T ] T z z z ω ∈ C r \omega \in \mathbf{C}^{r} ω ∈ C r ζ , ω ∈ C n − r \zeta ,\omega \in \mathbf{C}^{n - r} ζ , ω ∈ C n − r A ~ x ~ = y ~ = [ B C 0 D ] [ z ζ ] = [ ω ω ] \widetilde{A}\widetilde{x} = \widetilde{y} = \left[ \begin{array}{ll}B & C\\ 0 & D \end{array} \right]\left[ \begin{array}{l}z\\ \zeta \end{array} \right] = \left[ \begin{array}{l}\omega \\ \omega \end{array} \right] A x = y = [ B 0 C D ] [ z ζ ] = [ ω ω ]
B z + C ζ = w , D ζ = ω . \begin{array}{l} B z + C \zeta = w, \\ D \zeta = \omega . \\ \end{array} B z + Cζ = w , D ζ = ω . 如果首先对 ζ \zeta ζ D ζ = ω D\zeta = \omega D ζ = ω ζ \zeta ζ z z z B z = w − C ζ Bz = w - C\zeta B z = w − Cζ
6.2.22 定义 如果矩阵 A ∈ M n A \in M_{n} A ∈ M n A A A
6.2.23 定理 矩阵 A ∈ M n A \in M_{n} A ∈ M n
( I + ∣ A ∣ ) n − 1 > 0 , (I + \mid A \mid) ^ {n - 1} > 0, ( I + ∣ A ∣ ) n − 1 > 0 , 或等价地,如果 [ I + M ( A ) ] n > 0 [I + M(A)]^n > 0 [ I + M ( A ) ] n > 0
证明:我们实际上要证明, A A A ( I + ∣ A ∣ ) n − 1 (I + |A|)^{n - 1} ( I + ∣ A ∣ ) n − 1 A A A P P P
A = P [ B C 0 D ] P T = P A ~ P T , A = P \left[ \begin{array}{l l} B & C \\ 0 & D \end{array} \right] P ^ {T} = P \tilde {A} P ^ {T}, A = P [ B 0 C D ] P T = P A ~ P T , 360
其中 B , C , 0 B, C, 0 B , C , 0 D D D P P P ∣ A ∣ = ∣ P A ~ P T ∣ = P ∣ A ~ ∣ P T |A| = |P\widetilde{A} P^{\mathrm{T}}| = P|\widetilde{A}|P^{\mathrm{T}} ∣ A ∣ = ∣ P A P T ∣ = P ∣ A ∣ P T ∣ A ~ ∣ 2 , ∣ A ~ ∣ 3 , ⋯ , ∣ A ~ ∣ n |\widetilde{A}|^{2}, |\widetilde{A}|^{3}, \cdots, |\widetilde{A}|^{n} ∣ A ∣ 2 , ∣ A ∣ 3 , ⋯ , ∣ A ∣ n A ~ \widetilde{A} A ( n − r ) × r (n - r)\times r ( n − r ) × r
( I + ∣ A ∣ ) n − 1 = ( I + P ∣ Λ ~ ∣ P T ) n − 1 = ( P [ I + ∣ Λ ~ ∣ ] P T ) n − 1 = P ( I + ∣ Λ ~ ∣ ) n − 1 P T = P [ I + ( n − 1 ) ∣ A ~ ∣ + ( n − 1 2 ) ∣ A ~ ∣ 2 + ⋯ + ( n − 1 n − 1 ) ∣ A ~ ∣ n − 1 ] P T , \begin{array}{l} (I + | A |) ^ {n - 1} = (I + P | \tilde {\Lambda} | P ^ {T}) ^ {n - 1} = (P [ I + | \tilde {\Lambda} | ] P ^ {T}) ^ {n - 1} = P (I + | \tilde {\Lambda} |) ^ {n - 1} P ^ {T} \\ = P \left[ I + (n - 1) \mid \tilde {A} \mid + \binom {n - 1} {2} \mid \tilde {A} \mid^ {2} + \dots + \binom {n - 1} {n - 1} \mid \tilde {A} \mid^ {n - 1} \right] P ^ {T}, \\ \end{array} ( I + ∣ A ∣ ) n − 1 = ( I + P ∣ Λ ~ ∣ P T ) n − 1 = ( P [ I + ∣ Λ ~ ∣ ] P T ) n − 1 = P ( I + ∣ Λ ~ ∣ ) n − 1 P T = P [ I + ( n − 1 ) ∣ A ~ ∣ + ( 2 n − 1 ) ∣ A ~ ∣ 2 + ⋯ + ( n − 1 n − 1 ) ∣ A ~ ∣ n − 1 ] P T , 361
且上述方括号中的所有项在其左下角都有 ( n − r ) × r (n - r) \times r ( n − r ) × r ( I + ∣ A ∣ ) n − 1 (I + |A|)^{n-1} ( I + ∣ A ∣ ) n − 1
反之,假定对某个 p ≠ q p \neq q p = q ( I + ∣ A ∣ ) n − 1 (I + |A|)^{n-1} ( I + ∣ A ∣ ) n − 1 ( p , q ) (p, q) ( p , q ) Γ ( A ) \Gamma(A) Γ ( A ) P p P_p P p P q P_q P q
S 1 ≡ { P i : P i = P q 或 在 Γ ( A ) 中 有 一 条 从 P i 到 P q 的 道 路 } S _ {1} \equiv \{P _ {i}: P _ {i} = P _ {q} \text {或 在} \Gamma (A) \text {中 有 一 条 从} P _ {i} \text {到} P _ {q} \text {的 道 路} \} S 1 ≡ { P i : P i = P q 或 在 Γ ( A ) 中 有 一 条 从 P i 到 P q 的 道 路 } 又设 S 2 S_{2} S 2 Γ ( A ) \Gamma(A) Γ ( A ) S 1 S_{1} S 1 S 1 ∪ S 2 = { P 1 , ⋯ , P n } S_{1} \cup S_{2} = \{P_{1}, \cdots, P_{n}\} S 1 ∪ S 2 = { P 1 , ⋯ , P n } P ˙ q ∈ S 1 ≠ ∅ \dot{P}_{q} \in S_{1} \neq \emptyset P ˙ q ∈ S 1 = ∅ S 2 ≠ { P 1 , ⋯ , P n } S_{2} \neq \{P_{1}, \cdots, P_{n}\} S 2 = { P 1 , ⋯ , P n } S 2 S_{2} S 2 P i P_{i} P i S 1 S_{1} S 1 P j P_{j} P j S 1 S_{1} S 1 P i P_{i} P i P q P_{q} P q P i P_{i} P i S 1 S_{1} S 1 S 2 S_{2} S 2 S 1 S_{1} S 1 S 1 = { P ~ 1 , ⋯ , P ~ n } S_{1} = \{\tilde{P}_{1}, \cdots, \tilde{P}_{n}\} S 1 = { P ~ 1 , ⋯ , P ~ n } S 2 = { P ~ i + 1 , ⋯ , P ~ n } S_{2} = \{\tilde{P}_{i+1}, \cdots, \tilde{P}_{n}\} S 2 = { P ~ i + 1 , ⋯ , P ~ n }
A ~ = P T A P = [ B C 0 D ] , B ∈ M r , 0 ∈ M n − r , r , \tilde {A} = P ^ {T} A P = \left[ \begin{array}{l l} B & C \\ 0 & D \end{array} \right], \quad B \in M _ {r}, \quad 0 \in M _ {n - r, r}, A ~ = P T A P = [ B 0 C D ] , B ∈ M r , 0 ∈ M n − r , r , 因此 A A A [ I + M ( A ) ] n > 0 [I + M(A)]^{n} > 0 [ I + M ( A ) ] n > 0
我们作一下总结.
6.2.24 定理 设 A ∈ M n A \in M_{n} A ∈ M n
(a) A A A ( I + ∣ A ∣ ) n − 1 > 0 (I + |A|)^{n - 1} > 0 ( I + ∣ A ∣ ) n − 1 > 0 [ I + M ( A ) ] n − 1 > 0 [I + M(A)]^{n - 1} > 0 [ I + M ( A ) ] n − 1 > 0 Γ ( A ) \Gamma(A) Γ ( A ) A A A
6.2.25 定义 设 A ∈ M n A \in M_{n} A ∈ M n A A A A A A
(a) A A A A A A i = 1 , … , n i = 1, \dots, n i = 1 , … , n ∣ a n ∣ ⩾ R i ′ ( A ) |a_{n}| \geqslant R_{i}^{\prime}(A) ∣ a n ∣ ⩾ R i ′ ( A ) i i i ∣ a n ∣ > R r ′ ( A ) \left|a_{n}\right| > R_{r}^{\prime}(A) ∣ a n ∣ > R r ′ ( A )
练习 用例子说明,一个矩阵可能是不可约的和对角占优的,但不是不可约对角占优的。
采用现在的术语,可以重新表述“较好定理”(6.2.8)及其推论如下:
6.2.26 定理 设 A ∈ M n A \in M_{n} A ∈ M n λ \lambda λ G ( A ) G(A) G ( A ) λ \lambda λ A A A
6.2.27 推论(Taussky)设 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n
(a) A A A
(b) 如果所有 a n > 0 a_{n} > 0 a n > 0 A A A λ i \lambda_{i} λ i Re ( λ i ) > 0 \operatorname{Re}(\lambda_i) > 0 Re ( λ i ) > 0
(c) 如果 A A A A A A A A A A A A
6.2.28 推论 设 A ∈ M n A \in M_{n} A ∈ M n i i i
R i = ∑ j = 1 n ∣ a i j ∣ < ∥ A ∥ r , R _ {i} = \sum_ {j = 1} ^ {n} | a _ {i j} | < \| A \| _ {r}, R i = j = 1 ∑ n ∣ a ij ∣ < ∥ A ∥ r , 即不是所有绝对行和等于极大绝对行和. 则 ρ ( A ) < ∥ A ∥ ∞ \rho(A) < \|A\|_{\infty} ρ ( A ) < ∥ A ∥ ∞ p 1 , ⋯ , p n > 0 p_1, \cdots, p_n > 0 p 1 , ⋯ , p n > 0
D = diag ( p 1 , p 2 , … , p n ) , D = \operatorname {d i a g} \left(p _ {1}, p _ {2}, \dots , p _ {n}\right), D = diag ( p 1 , p 2 , … , p n ) , 又如果对 i i i R i ( D − 1 A D ) < ∥ D − 1 A D ∥ R_{i}(D^{-1}AD) < \left\| D^{-1}AD\right\| R i ( D − 1 A D ) < D − 1 A D ρ ( A ) < ∥ D − 1 A D ∥ ∞ \rho(A) < \left\| D^{-1}AD\right\|_{\infty} ρ ( A ) < D − 1 A D ∞
证明:我们总有界 ρ ( A ) ⩽ ∥ A ∥ ∞ \rho(A) \leqslant \|A\|_{\infty} ρ ( A ) ⩽ ∥ A ∥ ∞ A A A λ \lambda λ ∣ λ ∣ = ∥ A ∥ ∞ |\lambda| = \|A\|_{\infty} ∣ λ ∣ = ∥ A ∥ ∞ λ \lambda λ R t < ∥ A ∥ ∞ R_t < \|A\|_{\infty} R t < ∥ A ∥ ∞ D − 1 A D D^{-1}AD D − 1 A D □ \square □
习题 证明不可约矩阵不可能有0行和0列
用例子说明推论(6.2.28)中的不可约性假设是必不可少的。
假定 A = [ a i j ] ∈ M n A = [a_{ij}] \in M_n A = [ a ij ] ∈ M n λ \lambda λ ∣ A ∣ ≡ [ ∣ a i j ∣ ] |A| \equiv [\mid a_{ij} \mid] ∣ A ∣ ≡ [ ∣ a ij ∣ ] x i > 0 x_i > 0 x i > 0 x = [ x 1 ] ∈ R n x = [x_1] \in \mathbb{R}^n x = [ x 1 ] ∈ R n ∣ A ∣ x = λ x |A| x = \lambda x ∣ A ∣ x = λ x D = diag ( x 1 , x 2 , … , x n ) D = \operatorname{diag}(x_1, x_2, \dots, x_n) D = diag ( x 1 , x 2 , … , x n ) D ′ ∣ A ∣ D D' \mid A \mid D D ′ ∣ A ∣ D λ \lambda λ D ′ A D D'AD D ′ A D
在第8章中将证明,具有正元素的方阵总有正特征值和相应的正特征向量。利用这一事实和上一个习题证明,只要 A A A
ρ ( A ) ⩽ ρ ( ∣ A ∣ ) . \rho (A) \leqslant \rho (\mid A \mid). ρ ( A ) ⩽ ρ ( ∣ A ∣ ) . 试用连续性证明, A A A A ∈ M n A \in M_{n} A ∈ M n
ρ ( A ) ⩽ ρ ( ∣ A ∣ ) . \rho (A) \leqslant \rho (\mid A \mid). ρ ( A ) ⩽ ρ ( ∣ A ∣ ) . 试用推论(6.2.28)证明,关于多项式
p ( z ) = z n + a n − 1 z n − 1 + ⋯ + a 1 z + a 0 , a 0 ≠ 0 p (z) = z ^ {n} + a _ {n - 1} z ^ {n - 1} + \dots + a _ {1} z + a _ {0}, \quad a _ {0} \neq 0 p ( z ) = z n + a n − 1 z n − 1 + ⋯ + a 1 z + a 0 , a 0 = 0 的根的 Cauchy 界 (5.6.40) 在不出现下述情形
∣ a 0 ∣ = ∣ a 1 ∣ + 1 = ∣ a 2 ∣ + 1 = ⋯ = ∣ a n − 1 ∣ + 1 \left| a _ {0} \right| = \left| a _ {1} \right| + 1 = \left| a _ {2} \right| + 1 = \dots = \left| a _ {n - 1} \right| + 1 ∣ a 0 ∣ = ∣ a 1 ∣ + 1 = ∣ a 2 ∣ + 1 = ⋯ = ∣ a n − 1 ∣ + 1 的假设下可稍许改进为
∣ z ˉ ∣ < max { ∣ a 0 ∣ , ∣ a 1 ∣ + 1 , ∣ a 2 ∣ + 1 , … , ∣ a n − 1 ∣ + 1 } . | \bar {z} | < \max \left\{\left| a _ {0} \right|, \left| a _ {1} \right| + 1, \left| a _ {2} \right| + 1, \dots , \left| a _ {n - 1} \right| + 1 \right\}. ∣ z ˉ ∣ < max { ∣ a 0 ∣ , ∣ a 1 ∣ + 1 , ∣ a 2 ∣ + 1 , … , ∣ a n − 1 ∣ + 1 } . 提示:证明,若 a 0 ≠ 0 a_0 \neq 0 a 0 = 0 C ( p ) C(p) C ( p )
进一步阅读 关于Levy-Desplanques定理的讨论以及许多有关的参考文献可参看O. Taussky, “A Recurring Theorem on Determinants,” Amer. Math. Monthly 56 (1949), 672-676.