7.4 收敛性分析

7.4.1 CG的收敛性

设 $x_{*}$ 是解析解, $x^{(m)} \in x^{(0)} + \mathcal{K}_m$ 是CG算法在 $x^{(0)} + \mathcal{K}_m$ 中找到的近似解, 即

x ^ {(m)} = \arg \min _ {x \in x ^ {(0)} + \mathcal {K} _ {m}} \| x - x _ {*} \| _ {A}.

记 $\mathbb{P}_k$ 为所有次数不超过 $k$ 的多项式的集合. 对任意 $x \in x^{(0)} + \mathcal{K}_m$ , 存在 $p(t) \in \mathbb{P}_{m-1}$ , 使得

x = x ^ {(0)} + p (A) r _ {0}.

于是有

x - x _ {*} = \varepsilon_ {0} + p (A) (b - A x ^ {(0)}) = \varepsilon_ {0} + p (A) (A x _ {*} - A x ^ {(0)}) = (I - A p (A)) \varepsilon_ {0} \triangleq q (A) \varepsilon_ {0},

其中 $\varepsilon_0 = x^{(0)} - x_*$ ，多项式 $q(t) = 1 - tp(t)\in \mathbb{P}_m$ 且 $q(0) = 1$ .所以

\left\| x - x _ {*} \right\| _ {A} ^ {2} = \varepsilon_ {0} ^ {\mathsf {T}} q (A) ^ {\mathsf {T}} A q (A) \varepsilon_ {0}.

设 $A = Q\Lambda Q^{\mathsf{T}}$ 是 $A$ 的特征值分解, 其中 $Q$ 是正交矩阵, $\Lambda = \mathrm{diag}(\lambda_1,\lambda_2,\dots ,\lambda_n)$ 是对角阵, 且 $\lambda_{i} > 0.$ 记 $y = [y_{1},y_{2},\ldots ,y_{n}]^{\mathsf{T}}\triangleq Q^{\mathsf{T}}\varepsilon_{0}$ , 则

\begin{array}{l} \| x ^ {(m)} - x _ {*} \| _ {A} ^ {2} = \min _ {x \in x ^ {(0)} + \mathcal {K} _ {m}} \| x - x _ {*} \| _ {A} ^ {2} \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \varepsilon_ {0} ^ {\top} q (A) ^ {\top} A q (A) \varepsilon_ {0} \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \varepsilon_ {0} ^ {\mathsf {T}} Q q (\Lambda) ^ {\mathsf {T}} \Lambda q (\Lambda) Q ^ {\mathsf {T}} \varepsilon_ {0} \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} y ^ {\mathsf {T}} q (\Lambda) ^ {\mathsf {T}} \Lambda q (\Lambda) y \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \sum_ {i = 1} ^ {n} y _ {i} ^ {2} \lambda_ {i} q (\lambda_ {i}) ^ {2} \\ \leq \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} \left\{q \left(\lambda_ {i}\right) ^ {2} \right\} \sum_ {i = 1} ^ {n} y _ {i} ^ {2} \lambda_ {i} \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} \left\{q \left(\lambda_ {i}\right) ^ {2} \right\} y ^ {\mathsf {T}} \Lambda y \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} \left\{q \left(\lambda_ {i}\right) ^ {2} \right\} \varepsilon_ {0} ^ {\top} A \varepsilon_ {0} \\ = \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} \left\{q \left(\lambda_ {i}\right) ^ {2} \right\} \| \varepsilon_ {0} \| _ {A} ^ {2}, \\ \end{array}

即

\frac {\left\| x ^ {(m)} - x _ {*} \right\| _ {A} ^ {2}}{\left\| x ^ {(0)} - x _ {*} \right\| _ {A} ^ {2}} \leq \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} \left\{q \left(\lambda_ {i}\right) ^ {2} \right\}.

因此, 我们有下面的结论

引理7.8 设 $A \in \mathbb{R}^{n \times n}$ 对称正定, $x^{(m)}$ 是CG算法迭代 $m$ 步后得到的近似解. 则

\frac {\left\| x ^ {(m)} - x _ {*} \right\| _ {A}}{\left\| x ^ {(0)} - x _ {*} \right\| _ {A}} \leq \min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {1 \leq i \leq n} | q (\lambda_ {i}) |. \tag {7.20}

由于 $A$ 的特征值通常是不知道的, 因此不等式 (7.19) 右端通常难以计算. 但在许多情况下, 我们可以通过一些近似方法估计出 $A$ 的最大特征值 $\lambda_{1}$ 和最小特征值 $\lambda_{n}$ . 假设 $\lambda_{1}$ 和 $\lambda_{n}$ 已知, 则不等式 (7.19) 右端可以放缩为

\min _ {q \in \mathbb {P} _ {m}, q (0) = 1} \max _ {\lambda_ {n} \leq \lambda \leq \lambda_ {1}} | q (\lambda) |. \tag {7.21}

由 Chebyshev 多项式的最佳逼近性质 (定理 6.33) 可知, 最小最大问题 (7.20) 的解为

q _ {*} (t) = \frac {T _ {m} \left(\frac {2 t - (\lambda_ {1} + \lambda_ {n})}{\lambda_ {1} - \lambda_ {n}}\right)}{T _ {m} \left(- \frac {\lambda_ {1} + \lambda_ {n}}{\lambda_ {1} - \lambda_ {n}}\right)},

其中 $T_{m}$ 为 $m$ 次 Chebyshev 多项式. 由于 $T_{m}(t) = (-1)^{m} T_{m}(t)$ , 且当 $|t| \leq 1$ 时有 $|T_{m}(t)| \leq 1$ , 所以

| q _ {*} (t) | \leq \frac {1}{T _ {m} \left(\frac {\lambda_ {1} + \lambda_ {n}}{\lambda_ {1} - \lambda_ {n}}\right)}.

又当 $|t| > 1$ 时

T _ {m} (t) = \frac {1}{2} \left[ \left(t + \sqrt {t ^ {2} - 1}\right) ^ {m} + \left(t + \sqrt {t ^ {2} - 1}\right) ^ {- m} \right] \geq \frac {1}{2} \left(t + \sqrt {t ^ {2} - 1}\right) ^ {m},

所以

\begin{array}{l} T _ {m} \left(\frac {\lambda_ {1} + \lambda_ {n}}{\lambda_ {1} - \lambda_ {n}}\right) \geq \frac {1}{2} \left(\frac {\lambda_ {1} + \lambda_ {n}}{\lambda_ {1} - \lambda_ {n}} + \sqrt {\frac {(\lambda_ {1} + \lambda_ {n}) ^ {2}}{(\lambda_ {1} - \lambda_ {n}) ^ {2}} - 1}\right) ^ {m} \\ = \frac {1}{2} \left(\frac {\lambda_ {1} + \lambda_ {n}}{\lambda_ {1} - \lambda_ {n}} + \frac {2 \sqrt {\lambda_ {1} \lambda_ {n}}}{\lambda_ {1} - \lambda_ {n}}\right) ^ {m} \\ = \frac {1}{2} \left(\frac {\sqrt {\lambda_ {1}} + \sqrt {\lambda_ {n}}}{\sqrt {\lambda_ {1}} - \sqrt {\lambda_ {n}}}\right) ^ {m} \\ = \frac {1}{2} \left(\frac {\sqrt {\kappa (A)} + 1}{\sqrt {\kappa (A)} - 1}\right) ^ {m}. \\ \end{array}

其中 $\kappa(A) = \frac{\lambda_1}{\lambda_n}$ 为 $A$ 的条件数. 因此我们可以得到下面的收敛性定理

定理7.9 设 $A \in \mathbb{R}^{n \times n}$ 对称正定, $x^{(m)}$ 是CG算法迭代 $m$ 步后得到的近似解. 则

\frac {\left\| x ^ {(m)} - x _ {*} \right\| _ {A}}{\left\| x ^ {(0)} - x _ {*} \right\| _ {A}} \leq 2 \left(\frac {\sqrt {\kappa (A)} - 1}{\sqrt {\kappa (A)} + 1}\right) ^ {m}. \tag {7.22}

7.4.2 CG的超收敛性

如果我们能够获得 $A$ 的更多的特征值信息, 则能得到更好的误差限 [6].

定理7.10 设 $A$ 对称正定, 特征值为

0 < \lambda_ {n} \leq \dots \leq \lambda_ {n + 1 - i} \leq b _ {1} \leq \lambda_ {n - i} \leq \dots \leq \lambda_ {j + 1} \leq b _ {2} \leq \lambda_ {j} \leq \dots \leq \lambda_ {1}.

则当 $m \geq i + j$ 时有

\frac {\left\| x ^ {(m)} - x _ {*} \right\| _ {A}}{\left\| x ^ {(0)} - x _ {*} \right\| _ {A}} \leq 2 \left(\frac {b - 1}{b + 1}\right) ^ {m - i - j} \max _ {\lambda \in [ b _ {1}, b _ {2} ]} \left\{\prod_ {k = n + 1 - i} ^ {n} \left(\frac {\lambda - \lambda_ {k}}{\lambda_ {k}}\right) \prod_ {k = 1} ^ {j} \left(\frac {\lambda_ {k} - \lambda}{\lambda_ {k}}\right) \right\}, \tag {7.23}

其中

b = \left(\frac {b _ {2}}{b _ {1}}\right) ^ {\frac {1}{2}} \geq 1.

由此可知, 当 $b_{1}$ 与 $b_{2}$ 非常接近时, 迭代 $i + j$ 步后, CG 算法收敛会非常快.

推论7.11 设 $A$ 对称正定, 特征值为

0 < \delta \leq \lambda_ {n} \leq \dots \leq \lambda_ {n + 1 - i} \leq 1 - \varepsilon \leq \lambda_ {n - i} \leq \dots \leq \lambda_ {j + 1} \leq 1 + \varepsilon \leq \lambda_ {j} \leq \dots \leq \lambda_ {1}.

则当 $m \geq i + j$ 时有

\frac {\left\| x ^ {(m)} - x _ {*} \right\| _ {A}}{\left\| x ^ {(0)} - x _ {*} \right\| _ {A}} \leq 2 \left(\frac {1 + \varepsilon}{\delta}\right) ^ {i} \varepsilon^ {m - i - j}. \tag {7.24}

7.4.3 GMRES的收敛性

正规矩阵情形

设 $A$ 是正规矩阵, 即

A = U \Lambda U ^ {*},

其中 $\Lambda = \mathrm{diag}(\lambda_1,\lambda_2,\ldots ,\lambda_n)$ 的对角线元素 $\lambda_{2}\in \mathbb{C}$ 为 $A$ 的特征值

设 $x \in x^{(0)} + \mathcal{K}_k(A, r_0)$ , 则存在多项式 $p(t) \in \mathbb{P}_{k-1}$ 使得 $x = x^{(0)} + p(A)r_0$ . 于是

b - A x = b - A x ^ {(0)} - A p (A) r _ {0} = (I - A p (A)) r _ {0} \triangleq q (A) r _ {0}, \tag {7.25}

其中 $q(t) = 1 - tp(t)\in \mathbb{P}_k$ 满足 $q(0) = 1$ .直接计算可知

\| b - A x \| _ {2} = \| q (A) r _ {0} \| _ {2} = \| U q (\Lambda) U ^ {*} r _ {0} \| _ {2} \leq \| U \| _ {2} \| U ^ {*} \| _ {2} \| q (\Lambda) \| _ {2} \| r _ {0} \| _ {2} = \| q (\Lambda) \| _ {2} \| r _ {0} \| _ {2}.

又 $\Lambda$ 是对角矩阵，所以

\| q(\Lambda)\|_{2} = \max_{1\leq i\leq n}|q(\lambda_{i})|.

设 $x^{(k)}$ 是近似解, 则由GMRES方法的最优性可知, $x^{(k)}$ 极小化残量的2-范数. 因此,

\begin{array}{l} \| b - A x ^ {(k)} \| _ {2} = \min _ {x \in x ^ {(0)} + \mathcal {K} _ {k} (A, r _ {0})} \| b - A x \| _ {2} \\ = \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \| q (A) r _ {0} \| _ {2} \\ \leq \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \| q (\Lambda) \| _ {2} \| r _ {0} \| _ {2} \\ = \| r_{0}\|_{2}\min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{1\leq i\leq n}|q(\lambda_{i})|. \\ \end{array}

于是, 我们有下面的结论

定理7.12 设 $A \in \mathbb{R}^{n \times n}$ 是正规矩阵, $x^{(k)}$ 是GMRES方法得到的近似解, 则

\frac {\| b - A x ^ {(k)} \| _ {2}}{\| r _ {0} \| _ {2}} \leq \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \max _ {1 \leq i \leq n} | q (\lambda_ {i}) |. \tag {7.26}

需要指出的是, 上界 (7.28) 是紧凑的 [60, 79]. 与 CG 算法类似, 我们也可以选取一个包含 $A$ 的所有特征值的区域 $\Omega \subset \mathbb{C}$ , 然后将定理 7.12 中的上界缩放为

\min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \max _ {\lambda \in \Omega} | q (\lambda) |. \tag {7.27}

通常 $\Omega$ 必须是连通的, 否则 (7.26) 的求解非常困难. 即使是两个区间的并都没法求解 [45]. 另外, $\Omega$ 不能包含原点.

我们首先考虑一种最简单的情形, 即 $\Omega$ 是复平面上的一个圆盘, 圆心为 $C(c,0)$ , 半径 $r > 0$ . 这里假定 $r < c$ , 因此原点不在 $\Omega$ 内.

定义复系数多项式 $q_{k}(z) = ((c - z) / c)^{k}$ ，则 $q_{k}(z)\in \mathbb{P}_{k}$ 且 $q_{k}(0) = 1$ .所以

\min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{1\leq i\leq n}|q(\lambda_{i})|\leq \max_{1\leq i\leq n}|q_{k}(\lambda_{i})| = \max_{1\leq i\leq n}\left|\frac{(c - \lambda_{i})^{k}}{c^{k}}\right|\leq \frac{r^{k}}{|c|^{k}}.

由此可见, 当 $r$ 越小或 $c$ 越大时, 右式趋向于 0 的速度就越快.

设 $A$ 是正规矩阵, 其特征值包含在一个圆盘内, 则圆盘的半径越小或者圆心离原点越远, 则 GMRES 收敛越快.

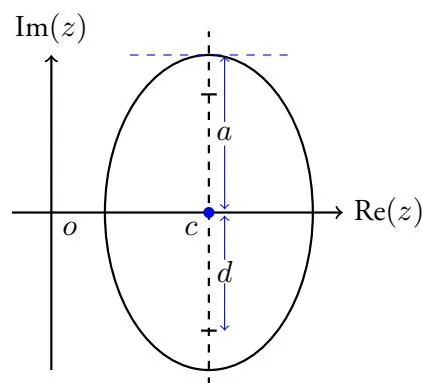
如果用椭圆来代替圆盘, 则可得出更紧凑的上界. 设 $A$ 的特征值全部包含在椭圆 $E(c, d, a)$ 内, 其中 $d > 0$ 为焦距, $a > 0$ 为半长轴长, $C(c, 0)$ 为椭圆中心. 并且假定原点不在椭圆内. 如下图所示.

令 $T_{k}$ 为 $k$ 次复 Chebyshev 多项式, 则多项式

\tilde {T} _ {k} (z) = \frac {T _ {k} (\frac {c - z}{d})}{T _ {k} (\frac {c}{d})}

就是极小极大问题

\min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \max _ {\lambda \in E (c, d, a)} | q (\lambda) | \tag {7.28}

的渐进最优解. 于是

\min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{1\leq i\leq n}|q(\lambda_{i})|\leq \min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{\lambda \in E(c,d,a)}|q(\lambda)|\leq \max_{\lambda \in E(c,d,a)}|\tilde{T}_{k}(\lambda)|.

由复 Chebyshev 多项式的性质可知

\max _ {\lambda \in E (c, d, a)} | \tilde {T} _ {k} (\lambda) | = \frac {T _ {k} (\frac {a}{d})}{| T _ {k} (\frac {c}{d}) |}.

因此

\min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{1\leq i\leq n}|q(\lambda_{i})|\leq \frac{T_{k}(\frac{a}{d})}{|T_{k}(\frac{c}{d})|}.

所以我们可得下面的结论

推论7.13 设 $A \in \mathbb{R}^{n \times n}$ 是正规矩阵, $x^{(k)}$ 是由GMRES得到的近似解, 则

\frac {\left\| b - A x ^ {(k)} \right\| _ {2}}{\left\| r _ {0} \right\| _ {2}} \leq \frac {T _ {k} \left(\frac {a}{d}\right)}{\left| T _ {k} \left(\frac {c}{d}\right) \right|}. \tag {7.29}

虽然 $\tilde{T}_k(z)$ 通常不是极小极大问题 (7.27) 的解, 但上界 (7.28) 却往往能给出 GMRES 方法收敛速度的一个很好的估计 [92].

非正规情形

当 $A$ 不是正规矩阵时, 在一般情况下, GMRES 方法的收敛性很难分析.

如果 $A\in \mathbb{R}^{n\times n}$ 是可对角化的，即

A = X \Lambda X ^ {- 1},

其中 $X\in \mathbb{C}^{n\times n}$ 非奇异, $\Lambda = \mathrm{diag}(\lambda_1,\lambda_2,\ldots ,\lambda_n)$ 的对角线元素 $\lambda_{i}\in \mathbb{C}$ 为 $A$ 的特征值, 则

\| b - A x ^ {(k)} \| _ {2} = \min _ {x \in x ^ {(0)} + \mathcal {K} _ {k} (A, r _ {0})} \| b - A x \| _ {2} = \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \| q (A) r _ {0} \| _ {2}. \tag {7.30}

相类似地, 我们可以得到下面的结论 [111].

定理7.14 设 $A = X \Lambda X^{-1}$ , 其中 $X \in \mathbb{C}^{n \times n}$ 非奇异, $\Lambda$ 是对角矩阵, $x^{(k)}$ 是GMRES方法得到的近似解, 则

\begin{array}{l} \frac{\|b - A x ^{(k)}\|_{2}}{\|r_{0}\|_{2}}\leq \| X\|_{2}\| X^{-1}\|_{2}\min_{q\in \mathbb{P}_{k}, q(0) = 1}\max_{1\leq i\leq n}|q(\lambda_{i})| \\ = \kappa (X) \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \max _ {1 \leq i \leq n} | q (\lambda_ {i}) |, \tag {7.31} \\ \end{array}

其中 $\kappa(X)$ 是 $X$ 的谱条件数.

如果 $A$ 接近正规, 则 $\kappa(X) \approx 1$ . 此时上界 (7.30) 在一定程度上能描述 GMRES 的收敛速度. 当如果 $X$ 远非正交, 则 $\kappa(X)$ 会很大, 此时该上界就失去实际意义了.

需要指出的是, 上面的分析并不意味着非正规矩阵就一定比正规矩阵收敛慢. 事实上, 对任意一个非正规矩阵, 总存在一个相应的正规矩阵, 使得 GMRES 方法的收敛速度是一样的 (假定初始残量相同) [3, 61, 62, 91].

虽然GMRES方法的收敛性与系数矩阵的特征值有关, 但显然并不仅仅取决于特征值的分布. 事实上, 我们有下面的结论.

定理7.15 对于任意给定的特征值分布和一条不增的收敛曲线, 则总存在一个矩阵 $A$ 和一个右端项 $b$ , 使得 $A$ 具有指定的特征值分布, 且 GMRES 方法的收敛曲线与给定的收敛曲线相同.

例7.1 考虑线性方程组 $Ax = b$ 其中

A = \left[ \begin{array}{c c c c c} 0 & 1 & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1 \\ a _ {0} & a _ {1} & a _ {2} & \dots & a _ {n - 1} \end{array} \right], \qquad b = e _ {1}.

当 $a_0 \neq 0$ 时, $A$ 非奇异. 易知, $A$ 的特征值多项式为

p (x) = \lambda^ {n} - a _ {n - 1} \lambda^ {n - 1} - a _ {n - 2} \lambda^ {n - 2} - \dots - a _ {1} \lambda - a _ {0}.

方程组的精确解为

x = \left[ - a _ {1} / a _ {0}, 1, 0, \dots , 0 \right] ^ {\mathsf {T}}.

以零向量为迭代初值, 则 GMRES 迭代到第 $n$ 步时才收敛. (前 $n - 1$ 步残量范数不变).

(GMRES_example01.m)

如果 $A$ 不可以对角化, 我们在分析 GMRES 方法的收敛性时, 通常会想办法用一个新的极小化问题来近似原来的极小化问题 (7.29). 当然, 这个新的极小化问题应该是比较容易求解的.

事实上, 我们有

\begin{array}{l} \frac {\| b - A x ^ {(k)} \| _ {2}}{\| r _ {0} \| _ {2}} = \frac {\min _ {q \in \mathbb {P} _ {k} , q (0) = 1} \| q (A) r _ {0} \| _ {2}}{\| r _ {0} \| _ {2}} \\ \leq \max _ {\| v \| _ {2} = 1} \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \| q (A) v \| _ {2} (7.32) \\ \leq \min _ {q \in \mathbb {P} _ {k}, q (0) = 1} \| q (A) \| _ {2}. (7.33) \\ \end{array}

不等式 (7.31) 右端代表的是在最坏情况下的 GMRES 收敛性, 而且是紧凑的, 即它是所能找到的不依赖于 $r_0$ 的最好上界. 但我们仍然不清楚, 到底是 $A$ 的那些性质决定着这个上界 [43].

可以证明, 当 $A$ 是正规矩阵时, 上界 (7.31) 和 (7.32) 是相等的 [60, 79]. 但是, 对于大多数非正规矩阵而言, 这两者是否相等或者非常接近, 迄今仍不太清楚.