5.4 分而治之法 分而治之 (Divide-and-Conquer, DC) 算法是由 Cuppen [28] 于 1981 年首次提出, 但直到 1995 年才出现稳定的实现方式 [66]. 该算法是目前计算大规模矩阵的所有特征值和特征向量的最快算法. 下面我们介绍该算法.
考虑不可约对称三对角矩阵
T = [ a 1 b 1 b 1 ⋱ ⋱ ⋱ a m − 1 b m − 1 b m − 1 a m b m b m a m + 1 b m + 1 b m + 1 ⋱ ⋱ ⋱ ⋱ b n − 1 b n − 1 a n ] = [ a 1 b 1 b 1 ⋱ ⋱ ⋱ a m − 1 b m − 1 b m − 1 a m − b m a m + 1 − b m b m + 1 b m + 1 ⋱ ⋱ b n − 1 b n − 1 ] + [ b m b m b m b m b n − 1 ] = [ T 1 0 0 T 2 ] + b m v v T , \begin{array}{l} T = \left[ \begin{array}{c c c c c c c c} a _ {1} & b _ {1} & & & \\ b _ {1} & \ddots & \ddots & & \\ & \ddots & a _ {m - 1} & b _ {m - 1} \\ & & b _ {m - 1} & a _ {m} & b _ {m} & & \\ \hline & & & b _ {m} & a _ {m + 1} & b _ {m + 1} & & \\ & & & & b _ {m + 1} & \ddots & \ddots & \\ & & & & & \ddots & \ddots & b _ {n - 1} \\ & & & & & & b _ {n - 1} & a _ {n} \end{array} \right] \\ = \left[ \begin{array}{c c c c c} a _ {1} & b _ {1} & & & \\ b _ {1} & \ddots & \ddots & & \\ & \ddots & a _ {m - 1} & b _ {m - 1} \\ & & b _ {m - 1} & a _ {m} - b _ {m} \\ \hline & & & a _ {m + 1} - b _ {m} & b _ {m + 1} \\ & & & b _ {m + 1} & \ddots \\ & & & & \ddots \\ & & & & b _ {n - 1} \\ & & & & b _ {n - 1} \end{array} \right] + \left[ \begin{array}{c c c c c} & & & \\ & & & \\ & & & \\ & b _ {m} & b _ {m} \\ \hline & b _ {m} & b _ {m} \\ & & \\ & b _ {n - 1} \end{array} \right] \\ = \left[ \begin{array}{c c} T _ {1} & 0 \\ \hline 0 & T _ {2} \end{array} \right] + b _ {m} v v ^ {\mathsf {T}}, \\ \end{array} T = a 1 b 1 b 1 ⋱ ⋱ ⋱ a m − 1 b m − 1 b m − 1 a m b m b m a m + 1 b m + 1 b m + 1 ⋱ ⋱ ⋱ ⋱ b n − 1 b n − 1 a n = a 1 b 1 b 1 ⋱ ⋱ ⋱ a m − 1 b m − 1 b m − 1 a m − b m a m + 1 − b m b m + 1 b m + 1 ⋱ ⋱ b n − 1 b n − 1 + b m b m b n − 1 b m b m = [ T 1 0 0 T 2 ] + b m v v T , 其中 v = [ 0 , … , 0 , 1 , 1 , 0 , … , 0 ] T v = [0,\dots ,0,1,1,0,\dots ,0]^{\mathsf{T}} v = [ 0 , … , 0 , 1 , 1 , 0 , … , 0 ] T T 1 T_{1} T 1 T 2 T_{2} T 2 T 1 = Q 1 Λ 1 Q 1 T , T_{1} = Q_{1}\Lambda_{1}Q_{1}^{\mathsf{T}}, T 1 = Q 1 Λ 1 Q 1 T , T 2 = Q 2 Λ 2 Q 2 T T_{2} = Q_{2}\Lambda_{2}Q_{2}^{\mathsf{T}} T 2 = Q 2 Λ 2 Q 2 T T T T
引理5.8 设 x , y ∈ R n x, y \in \mathbb{R}^n x , y ∈ R n det ( I + x y T ) = 1 + y T x \operatorname*{det}(I + xy^{\mathsf{T}}) = 1 + y^{\mathsf{T}}x det ( I + x y T ) = 1 + y T x
(留作练习)
我们首先考虑 T T T T 1 T_{1} T 1 T 2 T_{2} T 2
T = [ T 1 0 0 T 2 ] + b m v v T = [ Q 1 Λ 1 Q 1 T 0 0 Q 2 Λ 2 Q 2 T ] + b m v v T = [ Q 1 0 0 Q 2 ] ( [ Λ 1 0 0 Λ 2 ] + b m u u T ) [ Q 1 0 0 Q 2 ] T , \begin{array}{l} T = \left[ \begin{array}{c c} T _ {1} & 0 \\ 0 & T _ {2} \end{array} \right] + b _ {m} v v ^ {\mathsf {T}} = \left[ \begin{array}{c c} Q _ {1} \Lambda_ {1} Q _ {1} ^ {\mathsf {T}} & 0 \\ 0 & Q _ {2} \Lambda_ {2} Q _ {2} ^ {\mathsf {T}} \end{array} \right] + b _ {m} v v ^ {\mathsf {T}} \\ = \left[ \begin{array}{c c} Q _ {1} & 0 \\ 0 & Q _ {2} \end{array} \right] \left(\left[ \begin{array}{c c} \Lambda_ {1} & 0 \\ 0 & \Lambda_ {2} \end{array} \right] + b _ {m} u u ^ {\mathsf {T}}\right) \left[ \begin{array}{c c} Q _ {1} & 0 \\ 0 & Q _ {2} \end{array} \right] ^ {\mathsf {T}}, \\ \end{array} T = [ T 1 0 0 T 2 ] + b m v v T = [ Q 1 Λ 1 Q 1 T 0 0 Q 2 Λ 2 Q 2 T ] + b m v v T = [ Q 1 0 0 Q 2 ] ( [ Λ 1 0 0 Λ 2 ] + b m u u T ) [ Q 1 0 0 Q 2 ] T , 其中
u = [ Q 1 0 0 Q 2 ] T v = [ Q 1 T 的 最 后 一 列 Q 2 T 的 第 一 列 ] . u = \left[ \begin{array}{c c} {{Q _ {1}}} & {{0}} \\ {{0}} & {{Q _ {2}}} \end{array} \right] ^ {\mathsf {T}} v = \left[ \begin{array}{c} {{Q _ {1} ^ {\mathsf {T}} \text {的 最 后 一 列}}} \\ {{Q _ {2} ^ {\mathsf {T}} \text {的 第 一 列}}} \end{array} \right]. u = [ Q 1 0 0 Q 2 ] T v = [ Q 1 T 的 最 后 一 列 Q 2 T 的 第 一 列 ] . 令 α = b m , D = d i a g ( Λ 1 , Λ 2 ) = d i a g ( d 1 , d 2 , … , d n ) \alpha = b_{m}, D = \mathrm{diag}(\Lambda_{1},\Lambda_{2}) = \mathrm{diag}(d_{1},d_{2},\ldots ,d_{n}) α = b m , D = diag ( Λ 1 , Λ 2 ) = diag ( d 1 , d 2 , … , d n ) d 1 ≥ d 2 ≥ ⋯ ≥ d n d_1\geq d_2\geq \dots \geq d_n d 1 ≥ d 2 ≥ ⋯ ≥ d n T T T D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T
下面计算 D + α u u ⊤ D + \alpha uu^{\top} D + αu u ⊤ λ \lambda λ D + α u u ⊤ D + \alpha uu^{\top} D + αu u ⊤ D − λ I D - \lambda I D − λ I
det ( D + α u u T − λ I ) = det ( D − λ I ) ⋅ det ( I + α ( D − λ I ) − 1 u u T ) . \det (D + \alpha u u ^ {\mathsf {T}} - \lambda I) = \det (D - \lambda I) \cdot \det (I + \alpha (D - \lambda I) ^ {- 1} u u ^ {\mathsf {T}}). det ( D + αu u T − λ I ) = det ( D − λ I ) ⋅ det ( I + α ( D − λ I ) − 1 u u T ) . 故 det ( I + α ( D − λ I ) − 1 u u T ) = 0. \operatorname{det}(I + \alpha (D - \lambda I)^{-1}uu^{\mathsf{T}}) = 0. det ( I + α ( D − λ I ) − 1 u u T ) = 0.
det ( I + α ( D − λ I ) − 1 u u T ) = 1 + α u T ( D − λ I ) − 1 u = 1 + α ∑ i = 1 n u i 2 d i − λ ≜ f ( λ ) . \det (I + \alpha (D - \lambda I) ^ {- 1} u u ^ {\mathsf {T}}) = 1 + \alpha u ^ {\mathsf {T}} (D - \lambda I) ^ {- 1} u = 1 + \alpha \sum_ {i = 1} ^ {n} \frac {u _ {i} ^ {2}}{d _ {i} - \lambda} \triangleq f (\lambda). det ( I + α ( D − λ I ) − 1 u u T ) = 1 + α u T ( D − λ I ) − 1 u = 1 + α i = 1 ∑ n d i − λ u i 2 ≜ f ( λ ) . 故求 A A A f ( λ ) = 0 f(\lambda) = 0 f ( λ ) = 0
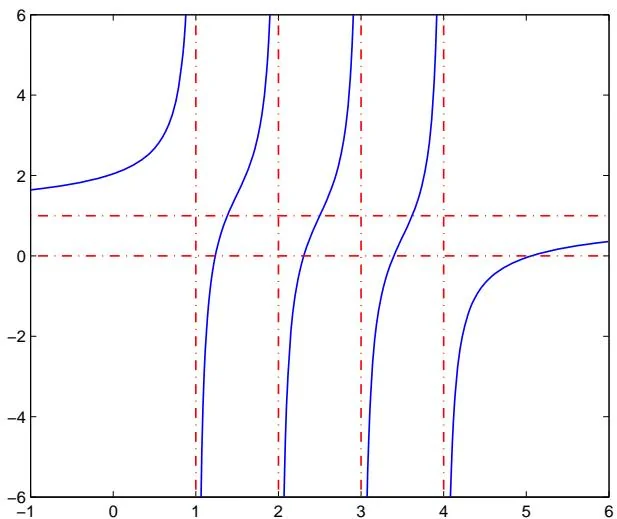
f ′ ( λ ) = α ∑ i = 1 n u i 2 ( d i − λ ) 2 , f ^ {\prime} (\lambda) = \alpha \sum_ {i = 1} ^ {n} \frac {u _ {i} ^ {2}}{(d _ {i} - \lambda) ^ {2}}, f ′ ( λ ) = α i = 1 ∑ n ( d i − λ ) 2 u i 2 , 当所有的 d i d_{i} d i u i u_{i} u i f ( λ ) f(\lambda) f ( λ ) λ ≠ d i \lambda \neq d_{i} λ = d i
f ( λ ) = 1 + 0.5 ( 1 4 − λ + 1 3 − λ + 1 2 − λ + 1 1 − λ ) f(\lambda) = 1 + 0.5\left(\frac{1}{4 - \lambda} +\frac{1}{3 - \lambda} +\frac{1}{2 - \lambda} +\frac{1}{1 - \lambda}\right) f ( λ ) = 1 + 0.5 ( 4 − λ 1 + 3 − λ 1 + 2 − λ 1 + 1 − λ 1 )
所以 f ( λ ) f(\lambda) f ( λ ) ( d i + 1 , d i ) (d_{i + 1},d_i) ( d i + 1 , d i ) n − 1 n - 1 n − 1 ( d 1 , ∞ ) (d_1,\infty) ( d 1 , ∞ ) α > 0 \alpha >0 α > 0 ( − ∞ , d n ) (- \infty ,d_n) ( − ∞ , d n ) α < 0 \alpha < 0 α < 0 f ( λ ) f(\lambda) f ( λ ) ( d i + 1 , d i ) (d_{i + 1},d_i) ( d i + 1 , d i ) ( α > 0 ) (\alpha >0) ( α > 0 ) ( α < 0 ) (\alpha < 0) ( α < 0 ) O ( n ) \mathcal{O}(n) O ( n ) D + α u u ⊤ D + \alpha uu^{\top} D + αu u ⊤ O ( n 2 ) \mathcal{O}(n^2) O ( n 2 )
当所有特征值计算出来后, 我们可以利用下面的引理来计算特征向量.
引理5.9设 D ∈ R n × n D\in \mathbb{R}^{n\times n} D ∈ R n × n u ∈ R n u\in \mathbb{R}^n u ∈ R n α ∈ R , \alpha \in \mathbb{R}, α ∈ R , λ \lambda λ D + α u u ⊤ D + \alpha uu^{\top} D + αu u ⊤ λ ≠ d i , \lambda \neq d_{i}, λ = d i , i = 1 , 2 , … , n , i = 1,2,\ldots ,n, i = 1 , 2 , … , n , ( D − λ I ) − 1 u (D - \lambda I)^{-1}u ( D − λ I ) − 1 u
证明. 由引理5.8可知
0 = det ( D + α u u T − λ I ) = det ( D − λ I ) ⋅ det ( I + α ( D − λ I ) − 1 u u T ) = det ( D − λ I ) ⋅ ( 1 + α u T ( D − λ I ) − 1 u ) , \begin{array}{l} 0 = \det (D + \alpha u u ^ {\mathsf {T}} - \lambda I) = \det (D - \lambda I) \cdot \det \left(I + \alpha (D - \lambda I) ^ {- 1} u u ^ {\mathsf {T}}\right) \\ = \det (D - \lambda I) \cdot \left(1 + \alpha u ^ {\mathsf {T}} (D - \lambda I) ^ {- 1} u\right), \\ \end{array} 0 = det ( D + αu u T − λ I ) = det ( D − λ I ) ⋅ det ( I + α ( D − λ I ) − 1 u u T ) = det ( D − λ I ) ⋅ ( 1 + α u T ( D − λ I ) − 1 u ) , 故 1 + α u T ( D − λ I ) − 1 u = 0 1 + \alpha u^{\mathsf{T}}(D - \lambda I)^{-1}u = 0 1 + α u T ( D − λ I ) − 1 u = 0 α u T ( D − λ I ) − 1 u = − 1. \alpha u^{\mathsf{T}}(D - \lambda I)^{-1}u = -1. α u T ( D − λ I ) − 1 u = − 1.
( D + α u u T ) ( ( D − λ I ) − 1 u ) = ( D − λ I + λ I + α u u T ) ( D − λ I ) − 1 u = u + λ ( D − λ I ) − 1 u + ( α u T ( D − λ I ) − 1 u ) u = u + λ ( D − λ I ) − 1 u − u = λ ( D − λ I ) − 1 u , \begin{array}{l} \left(D + \alpha u u ^ {\mathsf {T}}\right) \left(\left(D - \lambda I\right) ^ {- 1} u\right) = \left(D - \lambda I + \lambda I + \alpha u u ^ {\mathsf {T}}\right) \left(D - \lambda I\right) ^ {- 1} u \\ = u + \lambda (D - \lambda I) ^ {- 1} u + (\alpha u ^ {\mathsf {T}} (D - \lambda I) ^ {- 1} u) u \\ = u + \lambda (D - \lambda I) ^ {- 1} u - u \\ = \lambda (D - \lambda I) ^ {- 1} u, \\ \end{array} ( D + αu u T ) ( ( D − λ I ) − 1 u ) = ( D − λ I + λ I + αu u T ) ( D − λ I ) − 1 u = u + λ ( D − λ I ) − 1 u + ( α u T ( D − λ I ) − 1 u ) u = u + λ ( D − λ I ) − 1 u − u = λ ( D − λ I ) − 1 u , 即引理结论成立.
算法5.5.计算对称三对角矩阵的特征值和特征向量的分而治之法(函数形式)
1: function [ Q , Λ ] = e i g _ d c ( T ) % T = Q Λ Q ⊤ [Q, \Lambda] = \mathbf{eig\_dc}(T) \quad \% T = Q\Lambda Q^{\top} [ Q , Λ ] = eig_dc ( T ) % T = Q Λ Q ⊤ T T T 1 × 1 1 \times 1 1 × 1 Q = 1 , Λ = T Q = 1, \Lambda = T Q = 1 , Λ = T T = [ T 1 0 0 T 2 ] + b m v v T T = \left[ \begin{array}{cc}T_{1} & 0\\ 0 & T_{2} \end{array} \right] + b_{m}vv^{\mathsf{T}} T = [ T 1 0 0 T 2 ] + b m v v T [ Q 1 , Λ 1 ] = e i g _ d c ( T 1 ) [Q_1, \Lambda_1] = \mathbf{eig\_dc}(T_1) [ Q 1 , Λ 1 ] = eig_dc ( T 1 ) [ Q 2 , Λ 2 ] = e i g _ d c ( T 2 ) [Q_2, \Lambda_2] = \mathbf{eig\_dc}(T_2) [ Q 2 , Λ 2 ] = eig_dc ( T 2 ) D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T Λ 1 , Λ 2 , Q 1 , Q 2 \Lambda_1, \Lambda_2, Q_1, Q_2 Λ 1 , Λ 2 , Q 1 , Q 2 Λ \Lambda Λ Q ^ \hat{Q} Q ^ D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T T T T Q = [ Q 1 0 0 Q 2 ] ⋅ Q ^ Q = \begin{bmatrix} Q_1 & 0 \\ 0 & Q_2 \end{bmatrix} \cdot \hat{Q} Q = [ Q 1 0 0 Q 2 ] ⋅ Q ^
在分而治之法中, 特征值和特征向量是同时计算的.
实施细节 在实际使用分而治之算法时, 我们需要考虑以下几个细节问题:
(1) 如何减小运算量;f ( λ ) = 0 f(\lambda) = 0 f ( λ ) = 0
(1) 如何减小运算量——收缩技巧 (deflation)
分而治之算法的计算复杂性分析: 用 t ( n ) t(n) t ( n ) n n n
t ( n ) = 2 t ( n / 2 ) t(n) = 2t(n / 2) t ( n ) = 2 t ( n /2 ) + c ⋅ n 3 +c\cdot n^{3} + c ⋅ n 3 Q Q Q
如果计算 Q Q Q c = 2 c = 2 c = 2
若不计 O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) t ( n ) = 2 t ( n / 2 ) + c ⋅ n 3 t(n) = 2t(n / 2) + c\cdot n^{3} t ( n ) = 2 t ( n /2 ) + c ⋅ n 3 t ( n ) ≈ c ⋅ 4 n 3 / 3. t(n)\approx c\cdot 4n^{3} / 3. t ( n ) ≈ c ⋅ 4 n 3 /3.
但事实上, 由于收缩 (deflation) 现象的存在, 常数 c c c
在前面的算法描述过程中, 我们假定 d i d_{i} d i u i u_{i} u i d i = d i + 1 d_{i} = d_{i + 1} d i = d i + 1 u i = 0 u_{i} = 0 u i = 0 d i d_{i} d i D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T d i − d i + 1 d_{i} - d_{i + 1} d i − d i + 1 ∣ u i ∣ |u_{i}| ∣ u i ∣ d i d_{i} d i D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T
在实际计算中, 收缩现象会经常发生, 而且非常频繁, 所以我们可以而且应该利用这种优点加快分而治之算法的速度 [28, 110].
由于主要的计算量集中在计算 Q Q Q u i = 0 u_{i} = 0 u i = 0 d i d_{i} d i e i e_i e i Q ^ \hat{Q} Q ^ i i i e i e_i e i Q Q Q i i i d i = d i + 1 d_{i} = d_{i + 1} d i = d i + 1
(2) 特征方程求解 通常我们可以使用牛顿法来计算特征方程 f ( λ ) = 0 f(\lambda) = 0 f ( λ ) = 0
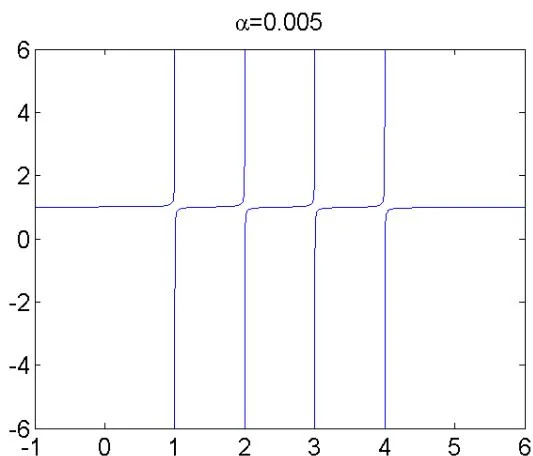
当 d i ≠ d i + 1 d_{i} \neq d_{i+1} d i = d i + 1 u i ≠ 0 u_{i} \neq 0 u i = 0 f ( λ ) f(\lambda) f ( λ ) ( d i + 1 , d i ) (d_{i+1}, d_{i}) ( d i + 1 , d i ) λ i \lambda_{i} λ i ∣ u i ∣ |u_{i}| ∣ u i ∣ d i d_{i} d i λ i \lambda_{i} λ i u i u_{i} u i f ( λ ) f(\lambda) f ( λ ) [ d i + 1 , d i ] [d_{i+1}, d_{i}] [ d i + 1 , d i ] [ d i + 1 , d i ] [d_{i+1}, d_{i}] [ d i + 1 , d i ] [ d i + 1 , d i ] [d_{i+1}, d_{i}] [ d i + 1 , d i ]
f ( λ ) = 1 + 0.005 ( 1 4 − λ + 1 3 − λ + 1 2 − λ + 1 1 − λ ) f(\lambda) = 1 + 0.005\left(\frac{1}{4 - \lambda} +\frac{1}{3 - \lambda} +\frac{1}{2 - \lambda} +\frac{1}{1 - \lambda}\right) f ( λ ) = 1 + 0.005 ( 4 − λ 1 + 3 − λ 1 + 2 − λ 1 + 1 − λ 1 )
这时需要采用修正的牛顿法. 假设我们已经计算出 λ i \lambda_{i} λ i λ ~ \tilde{\lambda} λ ~ λ ~ \tilde{\lambda} λ ~ f ( λ ) f(\lambda) f ( λ ) λ ~ \tilde{\lambda} λ ~ f ( λ ) f(\lambda) f ( λ ) f ( λ ) f(\lambda) f ( λ )
当 u i u_{i} u i h ( λ ) h(\lambda) h ( λ ) f ( λ ) f(\lambda) f ( λ ) h ( λ ) h(\lambda) h ( λ ) f ( λ ) f(\lambda) f ( λ )
关于 h ( λ ) h(\lambda) h ( λ ) h ( λ ) h(\lambda) h ( λ ) h ( λ ) h(\lambda) h ( λ ) h ( λ ) h(\lambda) h ( λ ) f ( λ ) f(\lambda) f ( λ )
当然, 这样的 h ( λ ) h(\lambda) h ( λ ) f ( λ ) f(\lambda) f ( λ ) ( d i + 1 , d i ) (d_{i+1}, d_i) ( d i + 1 , d i ) λ i \lambda_i λ i d i d_i d i d i + 1 d_{i+1} d i + 1 f ( λ ) f(\lambda) f ( λ )
h ( λ ) = c 1 d i − λ + c 2 d i + 1 − λ + c 3 , h (\lambda) = \frac {c _ {1}}{d _ {i} - \lambda} + \frac {c _ {2}}{d _ {i + 1} - \lambda} + c _ {3}, h ( λ ) = d i − λ c 1 + d i + 1 − λ c 2 + c 3 , 其中 c 1 , c 2 , c 3 c_{1}, c_{2}, c_{3} c 1 , c 2 , c 3 h ( λ ) h(\lambda) h ( λ ) c 1 , c 2 , c 3 c_{1}, c_{2}, c_{3} c 1 , c 2 , c 3 h ( λ ) h(\lambda) h ( λ ) λ ~ \tilde{\lambda} λ ~ f ( λ ) f(\lambda) f ( λ ) f ( λ ) f(\lambda) f ( λ )
f ( λ ) = 1 + α ∑ k = 1 n u k 2 d k − λ = 1 + α ( ∑ k = 1 i u k 2 d k − λ + ∑ k = i + 1 n u k 2 d k − λ ) ≜ 1 + α ( Ψ 1 ( λ ) + Ψ 2 ( λ ) ) . f (\lambda) = 1 + \alpha \sum_ {k = 1} ^ {n} \frac {u _ {k} ^ {2}}{d _ {k} - \lambda} = 1 + \alpha \left(\sum_ {k = 1} ^ {i} \frac {u _ {k} ^ {2}}{d _ {k} - \lambda} + \sum_ {k = i + 1} ^ {n} \frac {u _ {k} ^ {2}}{d _ {k} - \lambda}\right) \triangleq 1 + \alpha \big (\Psi_ {1} (\lambda) + \Psi_ {2} (\lambda) \big). f ( λ ) = 1 + α k = 1 ∑ n d k − λ u k 2 = 1 + α ( k = 1 ∑ i d k − λ u k 2 + k = i + 1 ∑ n d k − λ u k 2 ) ≜ 1 + α ( Ψ 1 ( λ ) + Ψ 2 ( λ ) ) . 当 λ ∈ ( d i + 1 , d i ) \lambda \in (d_{i + 1}, d_i) λ ∈ ( d i + 1 , d i ) Ψ 1 ( λ ) \Psi_1(\lambda) Ψ 1 ( λ ) Ψ 2 ( λ ) \Psi_2(\lambda) Ψ 2 ( λ ) h ( λ ) h(\lambda) h ( λ )
h ( λ ) = 1 + α ( h 1 ( λ ) + h 2 ( λ ) ) , h (\lambda) = 1 + \alpha \big (h _ {1} (\lambda) + h _ {2} (\lambda) \big), h ( λ ) = 1 + α ( h 1 ( λ ) + h 2 ( λ ) ) , 其中
h 1 ( λ ) = c 1 d i − λ + c ^ 1 , h 2 ( λ ) = c 2 d i + 1 − λ + c ^ 2 h _ {1} (\lambda) = \frac {c _ {1}}{d _ {i} - \lambda} + \hat {c} _ {1}, \quad h _ {2} (\lambda) = \frac {c _ {2}}{d _ {i + 1} - \lambda} + \hat {c} _ {2} h 1 ( λ ) = d i − λ c 1 + c ^ 1 , h 2 ( λ ) = d i + 1 − λ c 2 + c ^ 2 满足
h 1 ( λ ~ ) = Ψ 1 ( λ ~ ) , h 1 ′ ( λ ~ ) = Ψ 1 ′ ( λ ~ ) , h _ {1} (\tilde {\lambda}) = \Psi_ {1} (\tilde {\lambda}), \quad h _ {1} ^ {\prime} (\tilde {\lambda}) = \Psi_ {1} ^ {\prime} (\tilde {\lambda}), h 1 ( λ ~ ) = Ψ 1 ( λ ~ ) , h 1 ′ ( λ ~ ) = Ψ 1 ′ ( λ ~ ) , h 2 ( λ ~ ) = Ψ 2 ( λ ~ ) , h 2 ′ ( λ ~ ) = Ψ 2 ′ ( λ ~ ) . h _ {2} (\tilde {\lambda}) = \Psi_ {2} (\tilde {\lambda}), \quad h _ {2} ^ {\prime} (\tilde {\lambda}) = \Psi_ {2} ^ {\prime} (\tilde {\lambda}). h 2 ( λ ~ ) = Ψ 2 ( λ ~ ) , h 2 ′ ( λ ~ ) = Ψ 2 ′ ( λ ~ ) . 即 h 1 ( λ ) h_1(\lambda) h 1 ( λ ) h 2 ( λ ) h_2(\lambda) h 2 ( λ ) Ψ 1 ( λ ) \Psi_1(\lambda) Ψ 1 ( λ ) Ψ 2 ( λ ) \Psi_2(\lambda) Ψ 2 ( λ )
{ c 1 = Ψ 1 ′ ( λ ~ ) ( d i − λ ~ ) 2 , c ^ 1 = Ψ 1 ( λ ~ ) − Ψ 1 ′ ( λ ~ ) ( d i − λ ~ ) , c 2 = Ψ 2 ′ ( λ ~ ) ( d i + 1 − λ ~ ) 2 , c ^ 2 = Ψ 2 ( λ ~ ) − Ψ 2 ′ ( λ ~ ) ( d i + 1 − λ ~ ) . (5.3) \left\{ \begin{array}{l} c _ {1} = \Psi_ {1} ^ {\prime} (\tilde {\lambda}) \left(d _ {i} - \tilde {\lambda}\right) ^ {2}, \quad \hat {c} _ {1} = \Psi_ {1} (\tilde {\lambda}) - \Psi_ {1} ^ {\prime} (\tilde {\lambda}) \left(d _ {i} - \tilde {\lambda}\right), \\ c _ {2} = \Psi_ {2} ^ {\prime} (\tilde {\lambda}) \left(d _ {i + 1} - \tilde {\lambda}\right) ^ {2}, \quad \hat {c} _ {2} = \Psi_ {2} (\tilde {\lambda}) - \Psi_ {2} ^ {\prime} (\tilde {\lambda}) \left(d _ {i + 1} - \tilde {\lambda}\right). \end{array} \right. \tag {5.3} ⎩ ⎨ ⎧ c 1 = Ψ 1 ′ ( λ ~ ) ( d i − λ ~ ) 2 , c ^ 1 = Ψ 1 ( λ ~ ) − Ψ 1 ′ ( λ ~ ) ( d i − λ ~ ) , c 2 = Ψ 2 ′ ( λ ~ ) ( d i + 1 − λ ~ ) 2 , c ^ 2 = Ψ 2 ( λ ~ ) − Ψ 2 ′ ( λ ~ ) ( d i + 1 − λ ~ ) . ( 5.3 ) 所以
h ( λ ) = 1 + α ( c ^ 1 + c ^ 2 ) + α ( c 1 d i − λ + c 2 d i + 1 − λ ) . (5.4) h (\lambda) = 1 + \alpha \left(\hat {c} _ {1} + \hat {c} _ {2}\right) + \alpha \left(\frac {c _ {1}}{d _ {i} - \lambda} + \frac {c _ {2}}{d _ {i + 1} - \lambda}\right). \tag {5.4} h ( λ ) = 1 + α ( c ^ 1 + c ^ 2 ) + α ( d i − λ c 1 + d i + 1 − λ c 2 ) . ( 5.4 ) 这就是迭代函数.
算法5.6.修正的Newton算法 1: set k = 0 k = 0 k = 0 λ 0 ∈ [ d i + 1 , d i ] \lambda_0\in [d_{i + 1},d_i] λ 0 ∈ [ d i + 1 , d i ] λ ~ = λ k \tilde{\lambda} = \lambda_{k} λ ~ = λ k c 1 , c 2 , c ^ 1 , c ^ 2 c_{1}, c_{2}, \hat{c}_{1}, \hat{c}_{2} c 1 , c 2 , c ^ 1 , c ^ 2 k = k + 1 k = k + 1 k = k + 1
6: compute the solution λ k \lambda_{k} λ k h ( λ ) h(\lambda) h ( λ )
(3) 计算特征向量的稳定算法 设 λ i \lambda_{i} λ i D + α u u ⊤ D + \alpha uu^{\top} D + αu u ⊤ ( D − λ i I ) − 1 u (D - \lambda_{i}I)^{-1}u ( D − λ i I ) − 1 u λ i \lambda_{i} λ i λ i + 1 \lambda_{i+1} λ i + 1 d i + 1 d_{i+1} d i + 1 λ i ∈ ( d i + 1 , d i ) \lambda_{i} \in (d_{i+1}, d_{i}) λ i ∈ ( d i + 1 , d i ) λ i + 1 ∈ ( d i + 2 , d i + 1 ) \lambda_{i+1} \in (d_{i+2}, d_{i+1}) λ i + 1 ∈ ( d i + 2 , d i + 1 ) d i + 1 − λ i d_{i+1} - \lambda_{i} d i + 1 − λ i d i + 1 − λ i + 1 d_{i+1} - \lambda_{i+1} d i + 1 − λ i + 1 ( D − λ i I ) − 1 u (D - \lambda_{i}I)^{-1}u ( D − λ i I ) − 1 u ( D − λ i + 1 I ) − 1 u (D - \lambda_{i+1}I)^{-1}u ( D − λ i + 1 I ) − 1 u
下面的定理可以解决这个问题. 详情参见 [64, 146].
定理5.10 (Löwner) 设对角阵 D = d i a g ( d 1 , d 2 , … , d n ) D = \mathrm{diag}(d_1, d_2, \ldots, d_n) D = diag ( d 1 , d 2 , … , d n ) d 1 > d 2 > ⋯ > d n d_1 > d_2 > \dots > d_n d 1 > d 2 > ⋯ > d n D ^ = D + u ^ u ^ ⊤ \hat{D} = D + \hat{u}\hat{u}^{\top} D ^ = D + u ^ u ^ ⊤ λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ 1 , λ 2 , … , λ n
λ 1 > d 1 > λ 2 > d 2 > ⋯ > λ n > d n , (5.5) \lambda_ {1} > d _ {1} > \lambda_ {2} > d _ {2} > \dots > \lambda_ {n} > d _ {n}, \tag {5.5} λ 1 > d 1 > λ 2 > d 2 > ⋯ > λ n > d n , ( 5.5 ) 则向量 u ^ \hat{u} u ^
∣ u ^ i ∣ = ( ∏ k = 1 n ( λ k − d i ) ∏ k = 1 , k ≠ i n ( d k − d i ) ) 1 / 2 . (5.6) \left| \hat {u} _ {i} \right| = \left(\frac {\prod_ {k = 1} ^ {n} \left(\lambda_ {k} - d _ {i}\right)}{\prod_ {k = 1 , k \neq i} ^ {n} \left(d _ {k} - d _ {i}\right)}\right) ^ {1 / 2}. \tag {5.6} ∣ u ^ i ∣ = ( ∏ k = 1 , k = i n ( d k − d i ) ∏ k = 1 n ( λ k − d i ) ) 1/2 . ( 5.6 ) (留作课外自习)
证明. 由引理5.8可知 D ^ \hat{D} D ^ λ ≠ d i , i = 1 , 2 , … , n \lambda \neq d_{i}, i = 1,2,\dots,n λ = d i , i = 1 , 2 , … , n
p ( λ ) = det ( D ^ − λ I ) = det ( D − λ I + u ^ u ^ T ) = det ( D − λ I ) ⋅ det ( I + ( D − λ I ) − 1 u ^ u ^ T ) = det ( D − λ I ) ⋅ ( 1 + u ^ ⊤ ( D − λ I ) − 1 u ^ ) = ( ∏ k = 1 n ( d k − λ ) ) ⋅ ( 1 + ∑ i = 1 n u ^ i 2 d i − λ ) = ∏ k = 1 n ( d k − λ ) + ∑ i = 1 n ( ∏ k = 1 , k ≠ i n ( d k − λ ) u ^ i 2 ) . (5.7) \begin{array}{l} p (\lambda) = \det (\hat {D} - \lambda I) = \det (D - \lambda I + \hat {u} \hat {u} ^ {\mathsf {T}}) \\ = \det (D - \lambda I) \cdot \det (I + (D - \lambda I) ^ {- 1} \hat {u} \hat {u} ^ {\mathsf {T}}) \\ = \det (D - \lambda I) \cdot \left(1 + \hat {u} ^ {\top} (D - \lambda I) ^ {- 1} \hat {u}\right) \\ = \left(\prod_ {k = 1} ^ {n} \left(d _ {k} - \lambda\right)\right) \cdot \left(1 + \sum_ {i = 1} ^ {n} \frac {\hat {u} _ {i} ^ {2}}{d _ {i} - \lambda}\right) \\ = \prod_ {k = 1} ^ {n} \left(d _ {k} - \lambda\right) + \sum_ {i = 1} ^ {n} \left(\prod_ {k = 1, k \neq i} ^ {n} \left(d _ {k} - \lambda\right) \hat {u} _ {i} ^ {2}\right). \tag {5.7} \\ \end{array} p ( λ ) = det ( D ^ − λ I ) = det ( D − λ I + u ^ u ^ T ) = det ( D − λ I ) ⋅ det ( I + ( D − λ I ) − 1 u ^ u ^ T ) = det ( D − λ I ) ⋅ ( 1 + u ^ ⊤ ( D − λ I ) − 1 u ^ ) = ( ∏ k = 1 n ( d k − λ ) ) ⋅ ( 1 + ∑ i = 1 n d i − λ u ^ i 2 ) = ∏ k = 1 n ( d k − λ ) + ∑ i = 1 n ( ∏ k = 1 , k = i n ( d k − λ ) u ^ i 2 ) . ( 5.7 ) 由于等式 ( \ref e q : 1 ) (\ref{eq:1}) ( \ref e q : 1 ) λ \lambda λ λ = d i \lambda = d_{i} λ = d i ( \ref e q : 2 ) (\ref{eq:2}) ( \ref e q : 2 )
又 λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ 1 , λ 2 , … , λ n D ^ \hat{D} D ^ p ( λ ) = ∏ k = 1 n ( λ k − λ ) p(\lambda) = \prod_{k=1}^{n} (\lambda_k - \lambda) p ( λ ) = ∏ k = 1 n ( λ k − λ )
det ( D ^ − λ I ) = ∏ k = 1 n ( λ k − λ ) . \det (\hat {D} - \lambda I) = \prod_ {k = 1} ^ {n} (\lambda_ {k} - \lambda). det ( D ^ − λ I ) = k = 1 ∏ n ( λ k − λ ) . 取 λ = d i \lambda = d_{i} λ = d i det ( D ^ − λ I ) \operatorname{det}(\hat{D} - \lambda I) det ( D ^ − λ I )
∏ k = 1 , k ≠ i n ( d k − d i ) u ^ i 2 = ∏ k = 1 n ( λ k − d i ) , \prod_ {k = 1, k \neq i} ^ {n} (d _ {k} - d _ {i}) \hat {u} _ {i} ^ {2} = \prod_ {k = 1} ^ {n} (\lambda_ {k} - d _ {i}), k = 1 , k = i ∏ n ( d k − d i ) u ^ i 2 = k = 1 ∏ n ( λ k − d i ) , 即
u ^ i 2 = ∏ k = 1 n ( λ k − d i ) ∏ k = 1 , k ≠ i n ( d k − d i ) . \hat {u} _ {i} ^ {2} = \frac {\prod_ {k = 1} ^ {n} (\lambda_ {k} - d _ {i})}{\prod_ {k = 1 , k \neq i} ^ {n} (d _ {k} - d _ {i})}. u ^ i 2 = ∏ k = 1 , k = i n ( d k − d i ) ∏ k = 1 n ( λ k − d i ) . 由交错性质可知,上式右边是正的,故定理结论成立
设 λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ 1 , λ 2 , … , λ n D + α u u T D + \alpha uu^{\mathsf{T}} D + αu u T α > 0 \alpha > 0 α > 0 α u \sqrt{\alpha} u α u
思考:如果 α < 0 \alpha < 0 α < 0
因此, 我们可以采用公式 (5.4) 来计算特征向量. 这样就尽可能地避免了出现分母很小的情形.
下面是计算矩阵 D + u u T D + uu^{\mathsf{T}} D + u u T
算法5.7. 计算矩阵 D + u u T D + uu^{\mathsf{T}} D + u u T 1: Compute the eigenvalues λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ 1 , λ 2 , … , λ n f ( λ ) = 0 f(\lambda) = 0 f ( λ ) = 0 u ^ i \hat{u}_i u ^ i λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ 1 , λ 2 , … , λ n D + u ^ u ^ T D + \hat{u}\hat{u}^{\mathsf{T}} D + u ^ u ^ T D + u ^ u ^ T D + \hat{u}\hat{u}^{\mathsf{T}} D + u ^ u ^ T
通过分析可以说明上述算法计算出来的 D + u ^ u ^ T D + \hat{u}\hat{u}^{\mathrm{T}} D + u ^ u ^ T D + u ^ u ^ T D + \hat{u}\hat{u}^{\mathrm{T}} D + u ^ u ^ T D + u u T D + uu^{\mathrm{T}} D + u u T
箭型分而治之法 分而治之算法于1981年被首次提出, 但直到1995年才由Gu和Eisenstat给出了一种快速稳定的实现方式, 称为箭型分而治之法 (Arrowhead Divide-and-Conquer, ADC). 他们做了大量的数值试验, 在试验中, 当矩阵规模不超过6时, 就采用对称QR迭代来计算特征值和特征向量. 在对特征方程求解时, 他们采用的是修正的有理逼近法. 数值结果表明, ADC算法的计算精度可以与其他算法媲美, 而计算速度通常比对称QR迭代快5至10倍, 比Cuppen的分而治之法快2倍. 详细介绍见[65, 66].