12.5_本章小结
12.5 本章小结
这就是本书的所有内容。即使在读完了前11章的内容后,还有许多的资源可以下载、阅读、思考和编译。随着异构计算平台的日趋成熟,学习GPU计算也显得非常重要。我们希望你能学习并掌握当前最主流的并行编程环境之一CUDA。而且,我们希望你能够进一步研究出一些新方法来与计算机交互,以及处理软件面临的日益增加的信息量。你的这些研究思想和技术将把GPU计算推向更高境地。
附录
高级原子操作
在第9章中介绍了原子操作的一些使用方法,以及如何通过原子操作使数百个线程对共享数据进行安全地并发修改。在本附录中,我们将介绍原子操作的一种高级用法,即实现锁定数据结构。表面上来看,这个主题似乎与之前介绍的内容一样,事实也确实如此。在本书中你已经学习了许多复杂的主题,而锁定数据结构也不会比这些主题更难。然而,为什么要把这部分内容放到附录中?我们暂时先不透露任何原因,如果你感兴趣,那么可以继续读下去,我们将在附录中给出解释。
A.1 回顾点积运算
在第5章中,我们看到了如何通过CUDA C来实现矢量点积运算。点积算法是归约算法的一种,这个算法通过以下步骤来计算两个输入矢量的点积:
1)线程块中的每个线程将输入矢量中的两个对应元素相乘,并将结果保存在共享内存中。
2)在一个线程块中将计算得到多个乘积,然后通过线程将这些乘积结果两两相加,并将结果保存回共享内存。每执行完一次相加后,得到结果的数量将是计算之前结果数量的一半(这正是“归约”这个名字的含义)。
3)最终,每个线程块都将得到一个临时和值,它会把这个值保存到全局内存中并退出。
4)如果共有N个并行线程块运行核函数,那么CPU将把N个值相加起来从而得到最终的点积。
如果你对这里给出的点积算法步感到有些陌生,那么可以花点时间重新回顾第5章的内容。如果你已经熟悉了点积运算的代码,那么可以将主要注意力放到算法的第4步。虽然该算法并不需要将大量数据复制到主机,也不需要在CPU上执行任何的计算,但将最终结果的计算步骤移到CPU完成却似乎是一种低效方式。
然而,这里的问题并不只是低效。考虑一种情况,其中点积运算只是某个操作序列中的一步。如果CPU正在执行其他的任务或者计算,并需要将每个操作都放在GPU上执行,那么将出现问题。、此时,程序将不得不停止GPU上的计算,将中间结果复制回到主机,在CPU上完成计算,并最终将结果再传回GPU,然后继续计算下一个核函数。
由于本附录的内容主要是关于原子操作的使用,并且我们已经指出了在最初点积算法中的问题,因此你应该能预计到接下来将要介绍的内容。我们尝试使用原子操作来解决点积运算中的问题,使得整个运算都可以在GPU上执行,而CPU则可以不受干扰地执行其他任务。在理想情况下,不是在步骤3中退出核函数并在步骤4中返回到CPU,而是每个线程块都将自己的临时结果相加到全局内存中的最终总和。如果每个临时结果都以原子方式相加起来,那么就不用担心可能发生冲突或者得到不确定的结果。由于我们已经在直方图运算中使用了一个atomicAdd()操作,因此看上去似乎可以选择这个操作来实现我们的设想。
然而,在计算功能集2.0之前,atomicAdd()只能在整数上运算。如果只计算整数矢量的点积,那么是没有问题的,但浮点矢量的计算却更为常见。然而,大部分的NVIDIA硬件并不支持在浮点数值上进行原子运算!但这种做法是有原因的,因此暂时还不要将GPU弃之不用。
原子操作只能确保,每个线程在完成读取-修改-写入的序列之前,将不会有其他的线程读取或者写入目标内存。然而,原子操作并不能确保这些线程将按照何种顺序执行,例如当有三个线程都执行加法运算时,加法运行的执行顺序可以为 ,也可以为 。这对于
整数来说是可以接受的,因为整数数学运算是可结合的,因此 。然而,浮点算法并非可结合的,因为中间结果可能被截断,因此 通常并不等于 。因此,浮点数值上的原子数学运算是否有用就值得怀疑,因为在像GPU这种多线程的环境中,这种运算将带来不确定的结果。许多应用程序都不允许在运行两次时得到不同的结果,因此在早期的硬件中,浮点数学运算并不是优先支持的功能。
然而,如果可以容忍在计算结果中存在某种程度的不确定性,那么仍然可以完全在GPU上实现归约运算。但是,我们首先需要通过某种方式来绕开原子浮点数学运算。在这个解决方案中仍将使用原子操作,但不是用于算术本身。
A.1.1 原子锁
在构建GPU直方图中,我们使用了atomicAdd()函数,这个函数在执行读取-修改-写入操作时不会被其他线程中断。你可以想象底层硬件是如何执行这个运算的:硬件锁定目标内存位置,并且当锁定时,其他任何线程都不能读取或者写入这个位置上的值。如果可以通过某种方式在CUDA C核函数中模拟这种锁定行为,那么就可以在相应的内存位置或者数据结构上执行任意运算。锁定机制的行为与CPU互斥体非常相似。如果你不熟悉互斥行为,也不要苦恼,互斥体并不比你到目前为止学到的内容复杂。
基本思想是:分配一小块内存作为互斥体。互斥体的行为就像控制对某个资源访问的交通信号灯。这个资源可以是一个数据结构,一个缓冲区,或者是一个需要以原子方式修改的内存位置。当某个线程从这个互斥体中读到0时,它会把这个值解释为“绿灯”,表示没有其他线程正在使用这块内存。因此,该线程可以锁定这块内存,并执行想要的修改,而不会受到其他线程的干扰。要锁定这个内存位置,线程将1写入到互斥体。1就表示“红灯”,这将防止其他竞争的线程锁定这个内存。然后,其他竞争线程必须等待直到互斥体的所有者线程将0写入到互斥体后才能尝试修改被锁定的内存。
实现锁定过程的代码可以像下面这样:
void lock(void){if( \*bufex $= = 0$ ){\*bufex $= 1$ ;//将1保存到锁}遗憾的是,在这段代码中存在着一个严重问题,这也是我们熟悉的一个问题:如果在线程读取到0并且还没有修改这个值之前,另一个线程将1写入到互斥体,那么会发生什么情况?也就是说,这两个线程都将检查mutex上的值,并判断其是否为0。然后,它们都将1写入到这个位置,从而告诉其他的线程,该结构已经被锁定了并不能修改。之后,这两个线程都认为它们拥有相应内存或者数据结构的所有,然后开始执行并不安全的修改操作。这肯定会
造成严重后果!
我们想要完成的操作很简单:将latex的值与0相比较,如果latex等于0时,则将1写入到这个位置。要正确地实现这个操作,整个运算都需要以原子方式执行,这样就可以确保当线程检查和更新latex的值时,不会有其他的线程进行干扰。在CUDA C中,这个操作可以通过函数atomicCAS()来实现,这是一个原子的比较-交换操作(Compare-and-Swap)。函数atomicCAS()的参数包括一个指向目标内存的指针,一个与内存中的值进行比较的值,以及一个当比较相等时保存到目标内存上的值。通过这个操作,我们可以实现一个GPU锁定函数,如下所示:
__device__void lock(void){ while(atomicCAS(mutex,0,1) $! = 0$ ); }调用atomicCAS()将返回位于mutex地址上的值。因此,while()循环会不断运行,直到atomicCAS发现mutex的值为0。当发现为0时,比较操作成功,并线程将把1写入到mutext。本质上来看,这个线程将在while()循环中自旋,直到它成功地锁定这个数据结构。我们将使用这种锁定机制来实现GPU散列表。然而,我们首先需要把代码封装在一个结构中,这样在点积应用程序中使用起来就更为整洁:
struct Lock {
int * mutex;
Lock( void ) {
int state = 0;
HANDLE_ERROR(udaMalloc( (void**)& mutex, sizeof(int) ) );
HANDLE_ERROR(udaMemcpy( mutex, &state, sizeof(int),udaMemcpyHostToDevice ) );
}
-Lock( void ) {
udaFree( mutex );
}
__device__ void lock( void ) {
while( atomicCAS( mutex, 0, 1) != 0 );
}
__device__ void unlock( void ) {
atomicExch( mutex, 0 );
}
};注意,在代码中通过atomicExch(mutex, 1)来重置 mutex的值。函数atomicExch()将读取 mutex的值,将其与第二个参数(在这里是1)进行交换,并返回它读到的值。为什么要使用一个原子函数来实现这个操作,而不是使用某种更简单的方法来重置 mutex的值?例如:
\*mutex $= 0$如果你认为不采用这种简单方法是因为某个复杂的原因,那我们将告诉你这种想法是错误的,因为这种简单的方法同样是有效的。那么为什么不使用这种更简单的方法?原子事务和常规的全局内存操作将采用不同的执行路径。如果同时使用原子操作和标准的全局内存操作,那么将使得unlock()与后面的lock()调用看上去似乎没有被同步。虽然这种混合使用的方式仍可以实现正确的功能,但为了增加应用程序的可读性,对于所有对互斥体的访问都应该使用相同的方式。因此,在使用原子语句来锁定资源后,同样应用使用原子语句来解锁资源。
A.1.2 修改点积运算:原子锁
在最早的点积运算示例中,唯一要修改的部分就是最后在CPU上执行的归约部分。在前一节中,我们介绍了如何在GPU上实现互斥体。Lock结构位于lock.h中,在修改后的点积示例中将包含这个头文件:
include "/common/book.h" #include "lock.h" #define imin(a,b) (a<b?a:b) const int $\mathrm{N} = 33\ast 1024\ast 1024$ const int threadsPerBlock $= 256$ const int blocksPerGrid $\equiv$ imin(32,(N+threadsPerBlock-1)/ threadsPerBlock);除了两处不同的地方外,点积核函数的开头部分与第5章中使用的核函数完全相同。其中一个不同之处是核函数的原型:
globalvoid dot( Lock lock, float \*a, float \*b, float \*c)在修改后的点积函数中,将Lock类型的变量,以及输入矢量和输出缓冲区传递给核函数。Lock将被用于在最后的累加步骤中控制对输出缓冲区的访问。另一处修改从函数原型中看不出来,但却与原型有关。之前,参数float *c是一个包含N个浮点数的缓冲区,其中每个线程块都将其计算得到的临时结果保存到相应的元素中。这个缓冲区将被复制到CPU以便计算最终的点积值。然而,现在的参数c将不再指向一个缓冲区,而是指向一个浮点数值,这个值表示a和b中矢量的点积。除了这些修改,核函数的开头与第5章完全一样:
__global__ void dot( Lock lock, float *a,float \*b,float \*c){ _shared__ float cache threadsPerBlock]; int tid $=$ threadIdx.x $^+$ blockIdx.x \*blockDim.x; int cacheIndex $=$ threadIdx.x; float temp $= 0$ while(tid $< \mathbb{N}$ { temp $+ =$ a[tid] \*b[tid]; tid $+ =$ blockDim.x \*gridDim.x; } //设置cache中相应位置上的值 cache[cacheIndex] $=$ temp; //对线程块中的线程进行同步 _syncthreads(); //对于归约运算来说,以下代码要求threadPerBlock必须是2的幂 int i $=$ blockDim.x/2; while(i! $= 0$ ){ if (cacheIndex $< \mathrm{i}$ ) cache[cacheIndex] $+ =$ cache[cacheIndex+i]; _syncthreads(); i/=2;在执行的这个位置时,每个线程块中的256个线程都已经把各自计算的乘积相加起来,并且保存到cache[0]中。现在,每个线程块都需要将其临时结果相加到c执行的内存位置上。为了安全地执行这个操作,我们将使用锁来控制对该内存位置的访问,因此每个线程在更新*c的值之前,要先获取这个锁。在将线程块的临时结果与c处的值相加后,将解锁互斥体,这样其他的线程可以继续累加它们的值。在将临时值与最终结果相加后,这个线程块将不再需要任何计算,因此从核函数中返回。
if (cacheIndex == 0) { lock.lock(); $\star c + =$ cache[0]; lock.unlock(); }函数main()非常类似于最初的实现,只是存在两个不同。首先,不需要像第5章那样为临时结果分配一个缓冲区,而只需分配一个浮点大小的空间:
int main(void) {float \*a,\*b,c=0; float \*dev_a,\*dev_b,\*dev_c; //在CPU上分配内存 a=(float\*)malloc(N\*sizeof(float)); b=(float\*)malloc(N\*sizeof(float)); //在GPU上分配内存
HANDLE_ERROR(udaMalloc( $\mathrm{(void**)}$ &dev_a, N\*sizeof(float)));
HANDLE_ERROR(udaMalloc( $\mathrm{(void**)}$ &dev_b, N\*sizeof(float)));
HANDLE_ERROR(udaMalloc( $\mathrm{(void**)}$ &dev_c, sizeof(float)));与第5章一样,初始化输入数组并将它们复制到GPU。但需要注意的是,在这个示例中多了一次复制操作:将0复制到dev_c,我们将在这个位置上累加最终的点积值。由于每个线程块都将读取这个值,然后将这个值与线程块的临时加和相加,并将结果保存回去,因此我们需要将初始值置为0以便得到正确的结果。
//用数据填充主机内存
for(int $\mathrm{i} = 0$ : $\mathrm{i} < \mathrm{N}$ ; $\mathrm{i + + })$ {a[i] $=$ i;b[i] $=$ i\*2;1//将数组‘a’和‘b’复制到GPU
HANDLE_ERROR(udaMemcpy( dev_a, a, N*size(float),udaMemcpyHostToDevice));
HANDLE_ERROR(udaMemcpy( dev_b, b, N*size(float),udaMemcpyHostToDevice));
HANDLE_ERROR(udaMemcpy( dev_c, &c, sizeof(float),udaMemcpyHostToDevice));剩下的工作就是声明Lock,调用核函数,并将结果复制回CPU。
Lock lock;
dot<<blocksPerGrid, threadsPerBlock>>>(lock, dev_a, dev_b, dev_c);
//将数组‘c’从GPU复制到CPU
HANDLE_ERROR(udaMemcpy(&c, dev_c, sizeof(float),udaMemcpyDeviceToHost));在第5章示例程序的这个位置上,我们将执行for()循环把所有临时和值相加起来。然而,这个计算已经在GPU上通过原子锁完成了,因此可以直接跳到结果校验和内存释放的代码:
define sum_squares(x) $(x^{*}(x + 1)^{*}(2^{*}x + 1) / 6)$ printf(“Does GPU value $8.6g = 8.6g?\backslash n$ ,c,2\*sum_squares(float)(N-1)));
//释放GPU上的内存
CUDAFree(dev_a);
CUDAFree(dev_b);
CUDAFree(dev_c);
//释放CPU上的内存
free(a);
free(b);由于我们无法通过某种方式来预测每个线程块按照何种顺序将其临时和值与最终结果相加,因此很可能(几乎是肯定的)最终结果的相加顺序与CPU上的相加顺序不同。由于浮点加法的非结合性,因此GPU上的最终结果与CPU上的最终结果之间很可能存在细微的差异。对于这个问题没有太多的解决方法,除非增加大段的代码来确保各个线程块以某种确定的顺序来获取锁,并且这个顺序与CPU上的求和顺序完全相同。如果你觉得有必要这么做,那么不妨一试。接下来,我们将继续介绍如何使用原子锁来实现另一种多线程的数据结构。
A.2 实现散列表
散列表是计算机科学中最重要也是最常用的数据结构之一,它在大量应用程序中都起着重要的作用。对于还不熟悉散列表的读者来说,我们在这里会简要介绍一下。数据结构的研究远比这里给出的内容要深入,但我们只是为了引出接下来的内容,因此将只做简单介绍。如果你已经熟悉了散列表的相关概念,那么可以直接跳到A.2.2节。
A.2.1 散列表简介
散列表是一种保存键-值二元组的数据结构。例如,词典就可以被视为一个散列表。词典中的每个单词都是一个键,并且每个单词都有一个相关的定义。这个定义就是与单词相关的值,这样,词典中的每个单词及其定义就构成了一个键-值二元组。然而,在使用散列表时,重要的是要将在查找与某个键的对应值时需要的时间降至最低。通常,这应该是一个常量时间。也就是说,给定某个键,无论在散列表中保存了多少个键/值二元组,找出与这个键相对应值的时间应该是不变的。
散列表根据与值相应的键,把值放入“桶(Bucket)”中。这种将键映射到值的方法通常被称为散列函数。好的散列函数可以把键均匀地映射到所有桶中,因为这种方式能够满足定长查找时间的要求,而不论有多少个值被添加到散列表中。
例如,考虑词典散列表。一个很容易想到的散列函数就是使用26个桶,并让每个桶对应于字母表中的一个字母。这个散列函数将查看键的第一个字母,并根据这个字母将放入26个桶中的某一个。在图A.1中给出了这个散列函数如何分配将一些单词放入桶中。
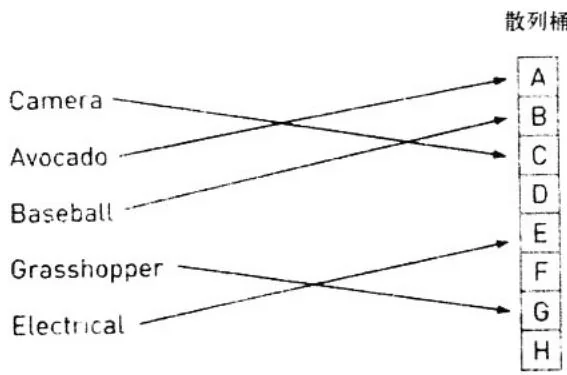
图A.1 通过散列函数将单词分配到各个桶中
我们都知道关于英语中单词的分布情况,这个散列函数远不能令人满意,因为它并不能把单词均匀地映射到26个桶中。在某些桶中包含了很少的键/值二元组,而在另一些桶中又包含大量的二元组。因此,如果某个单词的起始字母是一个常见字母,例如S,那么查找这个单词所花的时间将超过查找以X为起始字母的单词的时间。由于我们希望散列函数对于任意单词都实现定长的查找时间,因此这个结果是不能接受的。国内外有大量关于散列函数的研究,但本书并不会介绍所有这些技术。
散列表数据结构的最后一个问题是关于桶。如果有一个理想的散列函数,那么每个键都会被映射到一个不同的桶。在这种情况中,我们可以只将键/值二元组保存到一个数组中,并且数组中的每个元素都是一个桶。然而,即使这种理想的散列函数存在,在大多数情况下,我们仍需要处理各种冲突。当有多个键被映射到同一个桶时,就会发生冲突,例如将单词avocado和aardvark同时添加到词典散列表中。在一个桶中保存多个值的最简单方式是,将桶中的所有值保存到一个链表。当遇到冲突时,例如将aardvark添加到已经包含avocado的词典中时,只需将aardvark放到桶A的链表末尾,如图A.2所示。
在图A.2中添加了单词avocado后,第一个桶的链表中包含了一个键/值二元组。接下来又添加了aardvark,这个单词与avocado发生了冲突,因为这两个单词的起始字母都是A。你将注意
到,图A.3中的aardvark被放在第一个桶的链表末尾。
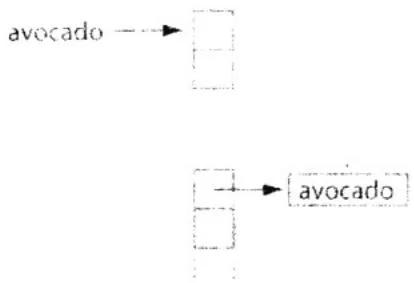
图A.2 将单词avocado插入到散列表
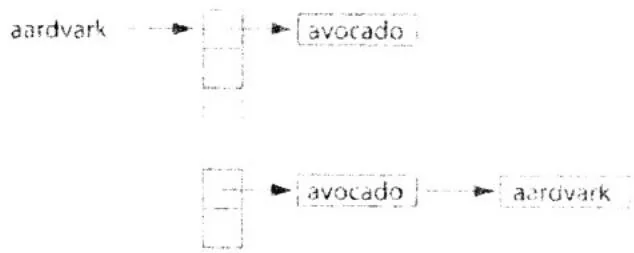
图A.3 解决当添加单词aardvark时发生的冲突
在了解了散列函数的一些概念和解决冲突的方式之后,我们接下来就来看如何实现散列表。
A.2.2 CPU散列表
在A.2.1节中介绍过,散列表主要包含两个部分:一个散列函数和一个表示桶的数据结构。桶的实现与之前完全一样:我们将分配一个长度为N的数组,并且数组中的每个元素都表示一个键/值二元组链表。在介绍散列函数之前,首先来看看数据结构:
include"../common/book.h"
struct Entry{ unsigned int key; void\* value; Entry \*next;
};
struct Table{ size_t count;Entry \*\*entries;
Entry \*pool;
Entry \*firstFree;
};正如在A.2.1节中描述的,Entry结构包含了一个键和一个值。在应用程序中,键是无符号整数。与键相关的值可以是任意数据类型,因此我们将value声明为一个void*变量。由于这个程序重点在于说明如何创建散列表数据结构,因此在value域中实际上不保存任何内容。为了保证完整性,我们将它包含在结构中,从而使你可以在自己的应用程序中使用这段代码。结构Entry的最后一个成员是指向下一个Entry节点的指针。在遇到冲突时,在同一个桶中将包含多个Entry节点,因此我们决定将这些对象保存为一个链表。因此,每个对象都将指向桶中的下一个节点,因而就形成了一个节点链表。最后一个Entry节点的next指针为NULL。
本质上,Table结构本身是一个“桶”数组。这个桶数组是一个长度为count的数组,其中entries中的每个桶都是一个指向某个Entry的指针。如果每添加一个Entry节点时都分配新的内存,那么将对程序的性能产生负面影响,为了避免这种情况,散列表将在成员pool中维持一个可用Entry节点的数组。firstFree这个域指向下一个可用的Entry节点,因此当需要将一个节点添加到散列表时,只需使用由firstFree指向的Entry,然后递增这个指针,就避免了新分配内存。注意,这种方式还将简化释放节点内存的代码,因为只需调用free()一次就可以释放所有这些节点。如果在每添加一个节点时都分配新的内存,那么就必须遍历散列表并依次释放每个节点。
在理解了数据结构后,我们来看一些其他的支持代码:
void initialize_table( Table &table, int entries, int elements ) { table.count = entries; table_entries = (Entry**)malloc( entries, sizeof Entry* ); table.pool = (Entry*)malloc( elements * sizeof Entry ); table.firstFree = table.pool; }在散列表的初始化过程中,主要操作包括为桶数组entries分配内存。我们还为节点池分配了内存,并将指针firstFree初始化为指向节点池数组中的第一个节点。
在程序的末尾,我们将释放已分配的内存,这将释放桶数组和空闲节点池:
void free_table(Table &table) { free(table_entries); free(table.pool); }在对散列表的简介中,我们提到了关于散列函数的不少内容。具体来说,我们讨论了一个好的散列函数在优秀的散列表和糟糕的散列表中将表现出不同的性能。在这个示例中,我们使
用了无符号整数作为键,并且需要将这些键映射到桶数组的索引。实现这个操作的最简单方式就是,将键作为索引。也就是说,将节点e保存在table_entries[e.key]中。然而,我们无法确保键的取值范围将小于桶数组的长度。幸运的是,这个问题的解决方法相对简单:
size_t hash(unsigned int key, size_t count) {
return key & count;
}既然散列函数非常重要,那么这个简单的函数能否实现我们的目标?理想情况是,我们希望将键均匀地映射到表中所有的桶,并且在这里采取的方式是将键对数组长度取模。在实际情况中,散列函数并不会这么简单,但由于这只是一个示例程序,因此将随机地生成我们的键。如果我们假设随机数值生成器生成的值大致是均匀的,那么这个散列函数应该将这些键均匀地映射到散列表的所有桶中。在你自己的散列表中,则可能需要一个更为复杂的散列函数。
在介绍了这个散列表结构以及散列函数后,接下来将介绍如何将键/值二元组添加到散列中。这个过程包括三个基本的步骤:
1)将键放入散列函数中计算出新节点所属的桶。
2)从节点池中取出一个预先分配的Entry节点,将初始化节点的key和value等域。
3)将这个节点插入到计算得到的桶的链表首部。
我们以一种直观的方式将这些步骤转换为代码。
void add_to_table( Table &table, unsigned int key, void* value)
{ //步骤1 size_t hashValue = hash(key, table.count); //步骤2 Entry *location = table.firstFree++; location->key = key; location->value = value; //步骤3 location->next = table_entries[hashValue]; table_entries[hashValue] = location; }如果之前没有见过链表(或者有段时间没见过了),那么在理解步骤3时可能会有些困难。链表的第一个节点被保存在table_entries[hashValue]中。在理解了这点后,就可以通过以下两个步骤在链表的头节点中插入一个新节点:首先,将新节点的next指针设置为指向链表的第一个节点。然后,将这个新节点保存到桶数组中,这样它将成为新链表的第一个节点。
为了判断这段代码能否工作,我们实现了一个函数对散列表执行完好性检查。在检查过程中将首先遍历这张表,并查看每个节点。将节点的键放入散列函数计算,并确认这个节点被保存到了正确的桶中。在检查了每个节点后,还要验证散列表中的节点数量确实等于添加到散列表的元素数量。如果这些数值并不相等,那么要么是无意中将一个节点添加到多个桶,要么没有正确地插入节点。
define SIZE (100*1024*1024)
#define ELEMENTS (SIZE / sizeof(unsigned int))
void verify_table(const Table &table){ int count $= 0$ . for(size_t $\mathrm{i} = 0$ ;i<table.count; $\mathrm{i + + )}$ { Entry \*current $=$ table_entries[i]; while(current != NULL){ ++count; if (hash(current->value, table.count) != i) printf( $"\% d$ hashed to $\% ld$ , but was located " "at $\% ld\backslash n$ ", current->value, hash(current->value, table.count), i); current $=$ current->next; } } if(count != ELEMENTS) printf("%d elements found in hash table.Should be %ld\n", count, ELEMENTS); else printf("All%d elements found in hash table.\n", count);
}暂时不考虑所有基础代码,我们先来看看main()。与书中的许多示例中一样,大部分复杂的功能都被放入辅助函数中,因此这个main()就变得相对简单:
define HASHENTRIES 1024
int main(void){ unsigned int \*buffer $=$ (unsigned int\*)big_random_block(SIZE); clock_t start,stop; start $=$ clock(); Table table; initialize_table(table,HASHENTRIES,ELEMENTS);for (int i=0; i<ELEMENTS; i++) {
add_to_table(table, buffer[i], (void*)NULL);
}
stop = clock();
float elapsedTime = (float)(stop - start) /
(float)CLOCKSEPERSEC * 1000.0f;
printf("Time to hash: %3.1f ms\n", elapsedTime);
verify_table(table);
free_table(table);
free(buffer);
return 0;你可以看到,首先分配了一大块内存来保存随机数值。这些随机生成的无符号整数将被作为插入到散列表中的键。在生成了这些数值后,接下来将读取系统时间以便统计程序的性能。我们对散列表进行初始化,然后通过for()循环将每个随机键插入到散列表。在添加了所有的键后,再次读取系统时间,通过之前读取的系统时间与这次系统时间就可以计算出在初始化和添加键上花费的时间。最后,我们通过完好性检查函数来验证散列表,并且释放了已分配的内存。
你可能已经注意到,每个键/值二元组中的值都是NULL。在应用程序中,键/值二元组中的值通常是某个有用的数据,但由于我们在这里主要关注散列表的实现本身,因此将使用一个无意义的值。
A.2.3 多线程环境下的散列表
在CPU散列表中包含的某些假设在GPU环境下将不再成立。首先,我们假设每次只有一个节点被添加到散列表中,这使得节点的插入操作更加简单。如果有多个线程试图同时将一个节点添加到散列表,那么我们最终将遇到与第9章多线程加法问题中类似的问题。
例如,重新回顾“avocado与aardvark”示例,并且想象一下,有两个线程A和B同时尝试将这些节点添加到散列表中。线程A在avocado上计算一个散列函数,线程B在aardvark计算散列函数。它们都计算得到同一个桶。在将新节点添加到链表时,线程A和B首先将它们新节点的next指针设置为指向线程链表中的第一个节点,如图A.4所示。
然后,这两个线程都尝试用它们各自的新节点替换桶中的节点。然而,只有第二个完成的线程才能将它的添加结果保存下来,因为它将覆盖前一个线程的工作。例如,线程A首先用avocado节点替换altitude节点。在添加完成后,线程B则用它的aardvark节点进行替换,并认为
被替换的节点仍然是altitude。然而,它现在替换的是avocado而不是altitude,结果就导致了图A.5中所示的情况。
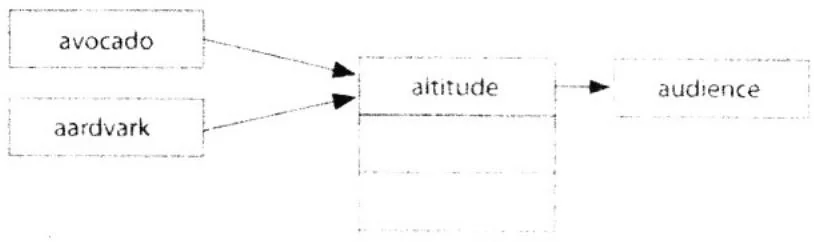
图A.4 多个线程都尝试将一个节点添加到同一个桶
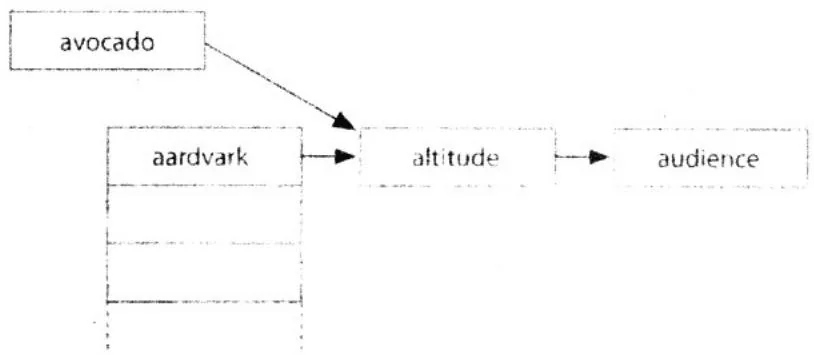
图A.5 在两个线程不正确地并发修改后得到的散列表
线程A的节点“漂浮在”散列表之外。幸运的是,在完好性检查函数中能发现并提示这个问题,因为它统计的节点小于我们预期的节点数量。然而,我们仍然需要回答这个问题:如何在GPU上构建一个散列表?我们观察到,每次只有一个线程可以安全地修改桶。这类似于前面的点积运算示例,在点积示例中,每次只有一个线程可以安全地将它的值与最终结果相加。如果每个桶都有一个相应的原子锁,那么我们可以确保每次只有一个线程对指定的桶进行修改。
A.2.4 GPU散列表
在有了某种方法来确保对散列表实现安全的多线程访问,我们可以继续实现在2.2节中GPU版本的散列表应用程序。我们需要包含头文件lock.h,其中包含了A.1.1节中对Lock结构的实现,我们需要把散列函数_声明为一个_device__函数。除了这些修改外,其他的重要数据结构和散列函数与CPU实现中的都相同。
include“../common/book.h"
include "lock.h"
struct Entry { unsigned int key; void\* value; Entry \*next;
};
struct Table{ size_t count; Entry \*\*entries; Entry \*pool;
}; _device_ host_ size_t hash( unsigned int value, size_t count){ return value & count;在上面的代码中使用了关键字__host__,当这个关键字与__device__一起使用时,将告诉NVIDIA编译器同时生成函数在设备上和主机上的版本。设备版本的函数将在设备上运行,并且只能从设备代码中调用。同样,主机版本的函数将在主机上运行,并且只能从主机代码中调用。如果在编写函数时,希望这个函数既可以在设备上使用,又可以在主机上使用,那么使用关键字__host__将是一种很方便的方式。
在初始化和释放散列表的过程中包含了与CPU版本中相同的步骤,但与之前的示例一样,我们使用CUDA运行时函数来实现这些步骤。我们使用CUDAAlloc()来分配一个桶数组和一个节点池,并使用cudaMemset()将桶数组节点初始化为0。为了在应用程序完成时释放这些内存,我们使用cudaFree()。
void initialize_table( Table &table, int entries, int elements ) { table.count = entries; HANDLE_ERROR(udaMemalloc( (void**)&tableentries, entries * sizeof Entry*)) ); HANDLE_ERROR(udaMemset( tableentries, 0, entries * sizeof Entry*) ); HANDLE_ERROR(udaMemalloc( (void**)&table.pool, elements * sizeof Entry) ); } void free_table( Table &table ) {udaFree( table.pool );udaFree( tableentries ); }在CPU实现中,我们通过一个函数来检查散列表的正确性。在GPU版本中需要一个类似的函数。我们可以编写一个在GPU上执行的verify_table(),或者可以使用在CPU版本中相同的代码,同时增加一个函数将散列表从GPU复制到CPU。虽然这两种方式都可以实现我们需要的功能,但第二种方式看上去更好,原因有两个:首先,它可以重用CPU版本的verify_table()。与其他的代码重用情况一样,这将节约开发时间,并且确保将来对代码进行修改时,对于两个版本的散列表只需修改一个地方。其次,在实现复制函数时将遇到一个有趣的问题,这个问题的解决方案在将来或许对你非常有用。
这里的verify_table()与CPU版本中的实现完全相同:
define SIZE (100*1024*1024)
#define ELEMENTS (SIZE / sizeof(unsigned int))
#define HASH_ENTRIES 1024
void verify_table(const Table &dev_table){ Table table; copy_table_to_host( dev_table, table ); int count $= 0$ . for(size_t i $\coloneqq 0$ ;i<table.count; $\mathrm{i + + }$ { Entry \*current $=$ table_entries[i]; while(current != NULL){ ++count; if (hash(current->value, table.count) != i) printf("%d hashed to %ld,but was located " "at%ld\n", current->value, hash(current->value, table.count), i); current $=$ current->next; } } if(count! $=$ ELEMENTS) printf( $"\% d$ elements found in hash table.Should be $\% l\mathrm{d}\backslash \mathrm{n}^{\prime \prime}$ count, ELEMENTS); else printf(“All%d elements found in hash table.\n",count); free(table.pool); free(table_entries);由于我们选择重用CPU版本中的verify_table(),因此需要一个函数将散列表从GPU内存复制到主机内存。这个函数包括三个步骤,其中前两个步骤相对简单,而第三个步骤则相对复杂一些。前两个步骤包括为散列表数据分配主机内存,并通过CUDAMemcpy()将GPU上的数据复制
到这块内存。我们已经多次编写了这段代码,因此并不困难。
void copy_table_to_host(const Table &table, Table &hostTable) {
hostTable.count = table.count;
hostTable_entries = (Entry**)malloc(table.count, sizeof(Entry));
hostTable.pool = (Entry*)malloc(ELEMENTS * sizeof(Entry));
HANDLE_ERROR(cudaMemcpy(hostTable_entries, table_entries, table.count * sizeof(Entry),udaMemcpyDeviceToHost));
HANDLE_ERROR(cudaMemcpy(hostTable.pool, table.pool, ELEMENTS * sizeof(Entry),udaMemcpyDeviceToHost));这个函数的复杂之处在于,在复制的数据中,有一部分数据是指针。我们不能简单地将这些指针复制到主机,因为这些指针指向的地址是在GPU上,它们在主机上并不是有效的指针。然而,这些指针的相对偏移仍然是有效的。每个指向Entry节点的GPU指针都指向数组table.pool[]中的某个位置,但为了在主机上使用散列表,我们需要它们指向数组hostTable.pool[]中相同的Entry。
给定一个GPU指针X,需要将这个指针相对于table.pool的偏移与hostTable.pool相加,从而获得一个有效的主机指针。也就是说,新指针应该按照以下公式计算:
(X - table.pool) + hostTable.pool对于每个被复制的Entry指针,都要执行这个更新操作:包括hostTable_entries中的Entry指针,以及散列表的节点池中每个Entry的next指针:
for (int i=0; i<table.count; i++) { if(hostTable_entries[i] != NULL) hostTable_entries[i] = (Entry*)(size_t)hostTable_entries[i] - (size_t)table.pool + (size_t)hostTable.pool); } for (int i=0; i<ELEMENTS; i++) { if(hostTable.pool[i].next != NULL) hostTable.pool[i].next = (Entry*)(size_t)hostTable.pool[i].next - (size_t)table.pool + (size_t)hostTable.pool); }在介绍完了数据结构、散列函数、初始化过程、内存释放过程以及验证代码后,还剩下的重要部分就是CUDA C原子语句的使用。核函数add_to_table()的参数包括一个键数组、一个值数组、散列表本身以及一个锁数组,这个数组将被用于锁定散列表中的每个桶。由于输入的数据是两个数组,并且在线程中需要对这两个数组进行索引,因此还需要将索引线性化:
__global__void add_to_table( unsigned int *keys, void **values, Table table, Lock *lock) { int tid = threadIdx.x + blockIdx.x * blockDim.x; int stride = blockDim.x * gridDim.x;线程会像点积示例那样遍历输入数组。对于数组key[]中的每个键,线程都将通过散列函数计算出这个键/值二元组属于哪个桶。在计算出目标桶之后,线程会锁定这个桶,添加它的键/值二元组,然后解锁这个桶。
while (tid < ELEMENTS) { unsigned int key = keys[tid]; size_t hashValue = hash(key, table.count); for (int i=0; i<32; i++) { if ((tid % 32) == i) { Entry *location = &(table.pool[tid]); location->key = key; location->value = values[tid]; lock[hashValue].lock(); location->next = table_entries[hashValue]; table_entries[hashValue] = location; lock[hashValue].unlock(); } } tid += stride; }然而,在这段代码中存在一个非常特别的地方,for()循环和后面的if()语句看上去显然是不必要的。在第6章中引入了线程束的概念。线程束是一个包含32个线程的集合,并且这些线程以步调一致的方式执行。在本书中并不讨论如何在GPU上实现这种步调一致的执行方式,但每次在线程束中只有一个线程可以获取这个锁,并且如果让线程束中的所有32个线程都同时竞争这个锁,那么将发生严重的问题。在这种情况下,最好的方式是在软件中执行一部分工作,遍历线程束中的线程,并给每个线程一次机会来获取数据结构的锁,执行它的工作,然后释放锁。
main()的执行流程看上去与CPU版本的相同。我们首先分配一大块随机数据作为散列表的键。然后,创建起始CUDA事件和停止CUDA事件,并且记录起始事件从而测试程序的性能。
接下来,继续为随机键数组分配GPU内存,将数组复制到GPU设备上并初始化散列表:
int main(void) { unsigned int \*buffer $=$ (unsigned int\*)big_random_block(SIZE);)、 CUDAEvent_t start,stop; HANDLE_ERROR( CUDAEventCreate( &start )); HANDLE_ERROR( CUDAEventCreate( &stop )); HANDLE_ERROR( CUDAEventRecord( start,0 )); unsigned int \*dev_keys; void \*\*dev_values; HANDLE_ERROR( CUDAAlloc( (void\*\*)&dev_keys,SIZE )); HANDLE_ERROR( CUDAAlloc( (void\*\*)&dev_values,SIZE )); HANDLE_ERROR( CUDAMemcpy( dev_keys,buffer,SIZE, CUDAMemcpyHostToDevice )); //在这里将值复制到dev_values Table table; initialize_table( table,HASHENTRIES,ELEMENTS);在构建散列表中的过程中,最后一个步骤就是为散列表的桶准备好锁。我们为散列表中每个桶都分配一个锁。显然,如果对于整个散列表都只使用一个锁,那么将节约大量的内存。但这么做将严重降低性能,因为当一组线程同时将节点添加到散列表时,每个线程都必须竞争散列表的锁。因此,我们声明了一个锁数组,数组中的每个锁对应于中桶数组中的每个桶。然后,我们为这些锁分配了一个GPU数组,并将它们复制到GPU设备上:
Lock lock[HASH_ENTRIES];
Lock *dev_lock;
HANDLE_ERROR(udaMalloc((void**)&dev_lock, HASH_ENTRIES * sizeof(Lock)));
HANDLE_ERROR(udaMemcpy(dev_lock, lock, HASH_ENTRIES * sizeof(Lock),udaMemcpyHostToDevice));main()的剩余部分类似于CPU版本:将键添加到散列表,停止性能计数器,验证散列表的正确性,并且执行内存释放工作。
add_to_table<<<60,256>>>(dev_keys,dev_values, table,dev_lock);
HANDLE_ERROR( CUDAEventRecord(stop,0));HANDLE_ERROR(udaEventSynchronize(stop)); float elapsedTime;
HANDLE_ERROR(udaEventElapsedTime(& elapsedTime, start, stop)); printf("Time to hash: %3.1f ms\n", elapsedTime);
verify_table(table);
HANDLE_ERROR(udaEventDestroy(start));
HANDLE_ERROR(udaEventDestroy(stop)); free_table(table);
CUDAFree(dev_lock);
CUDAFree(dev_keys);
CUDAFree(dev_values);
free(buffer);
return 0;A.2.5 散列表的性能
在Intel Core 2 Duo上,A.2.2节中在100MB的数据中构建散列表时需要360毫秒。在编译代码时使用了编译选项-03,以确保最大限度地优化CPU代码。A.2.4节中的多线程GPU散列表z在完成相同的任务时需要375毫秒。二者的差异小于百分之五,执行时间基本上大致相当,这就引出了一个问题:为什么像GPU这种大规模并行机器的性能还不如在CPU上执行的单线程应用程序?坦白地说,这是因为GPU并不是专门为了提升多线程对复杂数据结构(例如散列表)的访问性能而设计的。基于这个原因,在GPU上构建散列表这种数据结构很少是为了提升性能。因此,如果应用程序需要构建一个散列表或者类似的数据结构,那么最好在CPU上进行实现。
另一方面,你有时候会发现,在某个计算流水线中包括1到2个步骤,这些步骤在GPU上的执行性能并不比在CPU上的执行性能高。在这些情况中,你可以有三种选择:
在GPU上执行流水线的每个步骤。
在CPU上执行流水线的每个步骤。
在GPU上执行一些步骤,同时在GPU上执行另一些步骤。
最后一种方式似乎是最好的方式。然而,这就意味着,每当应用程序需要将计算从GPU移动到CPU,或者从CPU移动到GPU时,都需要对CPU和GPU进行同步。这种同步以及在主机和GPU之间的数据迁移通常会抵消采用混合方法时带来的性能优势。
在这种情况中,更好的方式或许是在GPU上执行每个步骤,即便算法的某些步骤并不适合使用GPU。GPU散列表可以减少一次CPU/GPU同步,这将把主机与GPU之间的数据传输量降至最低,并且使CPU能执行其他的计算。在这种情况中,在GPU的执行性能可能会好于在
CPU/GPU上混合执行的性能,尽管在某些步骤上GPU并不会比GPU更快(或者在某些情况中可能要慢于CPU)。
A.3 小结
我们在附录中介绍了如何使用原子的比较-交换操作来实现GPU互斥体。通过使用基于该互斥体构建的锁,我们介绍了如何将最初的点积应用程序修改为完全在GPU上运行。然后,我们基于这个思想进一步实现了一个多线程的散列表,并使用了一个锁数组来防止多个线程同时进行不安全的修改。事实上,我们实现的互斥体可以在任意并行数据结构中使用,并且通过自己的实践你会发现这个互斥体确实有用。当然,如果在应用程序中使用GPU来实现基于互斥体的数据结构,那么需要对应用程序的性能进行分析。GPU散列表的性能比CPU散列表的性能要更糟糕,因此只有在某些特定情况下,在这种类型的应用程序中使用GPU才是有意义的。在判断是只使用GPU,还是只使用CPU或者使用混合方法才能实现最优性能时,并没有固定的规则可供遵循,但如果知道如何使用原子语句,那么你就能根据具体的情况做出决策。
GPU高性能编程 CUDA实战
CUDA By Example
an Introduction to General-Purpose GPU Programming
对于开发基于GPU加速的并行计算系统的读者来说,本书绝对值得一读。
Jack Dongarra
田纳西大学杰出教授
美国橡树岭国家实验室杰出研究人员
CUDA是一种专门为提高并行程序开发效率而设计的计算架构。在构建高性能应用程序时,与综合性软件平台相结合,CUDA架构能充分发挥GPU的强大计算功能。很长时间以来,GPU一直用于图形和游戏应用程序中。但是现在,使用CUDA可将GPU用于科学计算、工程以及金融等其他应用领域。由于在CUDA中使用的编程语言只是一种对标准C语言进行简单扩展的语言,所以开发人员不需要具备任何计算机图形学的背景知识就可以掌握。
本书由CUDA软件平台小组的两位高级工程师撰写,向广大程序员介绍了如何使用这项新技术。作者通过多个示例详细介绍了CUDA开发中的方方面面。本书首先简要介绍了CUDA平台和架构,并快速介绍了CUDA C,随后详细介绍了CUDA每个功能中的关键技术与权衡因素。通过学习这些内容,你可以很清楚地了解CUDA中每个功能的适用场合,并编写出高性能的CUDA软件。
本书主要内容:
并行编程
线程协作
常量内存与事件
纹理内存
图形互操作
原子操作
流
多GPU上的CUDA
高级原子操作
其他CUDA资源
所需的CUDA软件工具均可以从NVIDIA公司的网站免费下载。
作者简介
Jason Sanders是NVIDIA公司CUDA平台小组的高级软件工程师,他参与了CUDA系统软件早期版本的开发,并参与了OpenCL1.0规范的制定,该规范是一个定义异构计算的行业标准。他曾经在ATI技术公司、Apple公司以及Novell公司工作过。
Edward Kandrot是NVIDIA公司CUDA平台小组的高级软件工程师。他在代码性能优化方面拥有20多年的工作经验,他曾经在Adobe公司、Microsoft公司以及Autodesk公司等工作过。
PEARSON
客服热线:(010)88378991,88361066
购书热线:(010)68326294,88379649,68995259
投稿热线:(010)88379604
读者信箱:hzjsj@hzbook.com

网上购书:www.china-pub.com
封面设计·锡彬

上架指导:计算机/程序设计
ISBN 978-7-111-32679-3
定价:39.00元
[General Information]
书名=GPU高性能编程CUDA实战
作者=(美)桑德斯著;聂雪军等译
页数=201
SS号=12804258
出版日期
出版社=机械工业出版社
原书定价
参考文献格式 (美)桑德斯著.GPU高性能编程CUDA实战.北京市:机械工业出版社,2011.01.
内容提要=CUDA是用来促进并行程序开发的一种计算架构。它与各种广泛的软件平台一起使用,使得程序员在构建高性能的应用程序的时候,可以借助图形处理单元(GPU)的强大力量。尽管GPU在图形和游戏编程领域应用多年,现在,CUDA使得开发其他领域的应用程序的程序员,也能够使用GPU的宝贵资源。本书由CUDA软件平台团队的两位高级成员撰写,介绍程序员如何利用这一新的技术。作者介绍了CUDA的各个方面,及其高级功能,还介绍了如何使用CUDA扩展,以及如何编写真正表现出优秀性能的CUDA软件。