59.4_正弦波的预测
59.4 正弦波的预测
基于以上实现,我们来尝试训练RNN。这里将包含噪声的正弦波作为数据集使用。我们可以使用dezero/datasets.py中的SinCurve类加载数据集,代码如下所示。
import numpy as np
importdezero
import matplotlib.pyplot as plt
train_set $=$ dezero.datasets.SinCurve(train=True)
print(len(train_set))
print(train_set[0])
print(train_set[1])
print(train_set[2])绘制图形
xs = [example[0] for example in train_set]
ts = [example[1] for example in train_set]
plt.plot(np.arange(len(xs)), xs, label='xs')
plt.plot(np.arange(len(ts)), ts, label='ts')
plt.show()运行结果
999
(array([-0.03458701]), array([0.01726473]))
(array([0.01726473]), array([0.04656735]))
(array([0.04656735]), array([0.03284844]))上面的代码输出了train_set的第0个、第1个和第2个数据。这些数据都是元组,元组的第1个元素是输入数据,第2个元素是训练数据(标签)。另外,上面的代码还可以绘制出图59-6这样的图形。
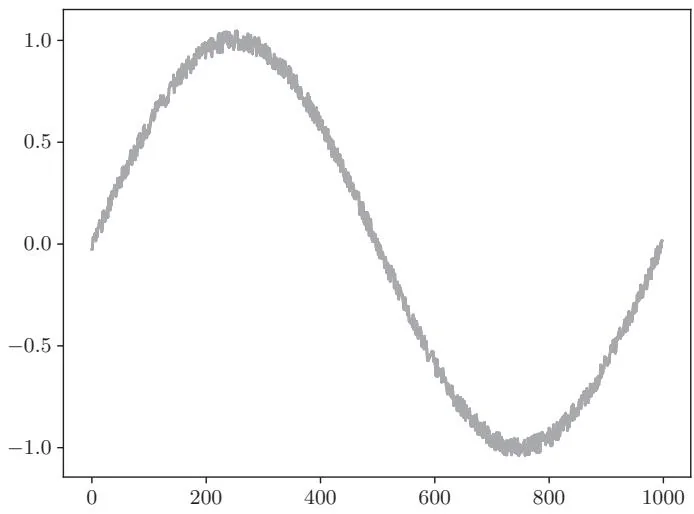
图59-6 正弦波数据集的plot图
从图59-6可以看出这是一个有噪声的正弦波。图中实际上绘制了xs和
ts这两组数据,但我们只能看到一条曲线。其实ts是xs的下一个时间步的数据,因此,图59-6中绘制的两条曲线几乎是相互重叠的。

正弦波数据集的训练数据是输入数据的未来一个时间步的数据。以上面的代码为例,二者的关系是 xs[1:] == ts[: -1]。这样的数据集可以用于预测时间序列数据的问题,即基于过去的数据预测下一个数据的问题。
下面用RNN来训练正弦波数据集,代码如下所示(省略了导入部分)。
steps/step59.py
设置超参数
max_epoch = 100
hidden_size = 100
bptt_length = 30 # BPTT的长度
train_set =dezeroDatasets.SinCurve(train=True)
seqlen = len(train_set)
model = SimpleRNN(hidden_size,1)
optimizer =dezero.trainers.Adam().setup(model)
#训练开始
for epoch in range(max_epoch):
model.reset_state()
loss, count = 0, 0
for x, t in train_set:
x = x.reshape(1,1) #①形状转换为(1,1)
y = model(x)
loss += F.mean_squared_error(y, t)
count += 1
#②调整Truncated_BPTT的时机
if count % bptt_length == 0 or count == seqlen:
model.cleargrads()
loss/backward()
loss.unchain_backward() #③切断连接
optimizer.update()
avg_loss = float(loss.data) / count
print(|epoch %d | loss %f' % (epoch + 1, avg_loss))下面只对以上代码补充3点内容。首先①处将x的形状转换为(1,1)。DeZero神经网络的输入数据必须是二阶张量或四阶张量(在使用CNN时)。因此,即使输入数据只有一个,也必须把它转换为(1,1)。
②处判断调用backward方法的时机——要么在数据流转了30次之后,要么在到达数据集的终点(末尾)时。最后③处通过unchain_backward方法切断RNN隐藏状态的连接。

通过调用 loss.backup_unchain(), 从 loss 开始回溯, 切断所有出现的变量的连接。因此, RNN 的隐藏状态的连接也被切断。
运行上面的代码可知,损失(loss)在稳步下降。下面我们来使用一下训练后的模型。这次将新的(无噪音的)余弦波作为输入数据,并尝试预测下一步的数值。代码如下所示,结果如图59-7所示。
steps/step59.py
import matplotlib.pyplot as plt
xs $=$ np.cos(np.linspace(0,4\*np.pi,1000))
model.reset_state() #重置模型
pred_list $= []$
withdezero.no_grad(): forx in xs: $\mathrm{x} =$ np.array(x).reshape(1,1) y $=$ model(x) pred_list.append(float(y.data))
plt.plot(np.arange(len(xs)),xs, label $\coloneqq$ 'y=cos(x))
plt.plot(np.arange(len(xs)),pred_list, label $\equiv$ 'predict')
plt.xlabel('x')
pltylabel('y')
plt.legend()
plt.show()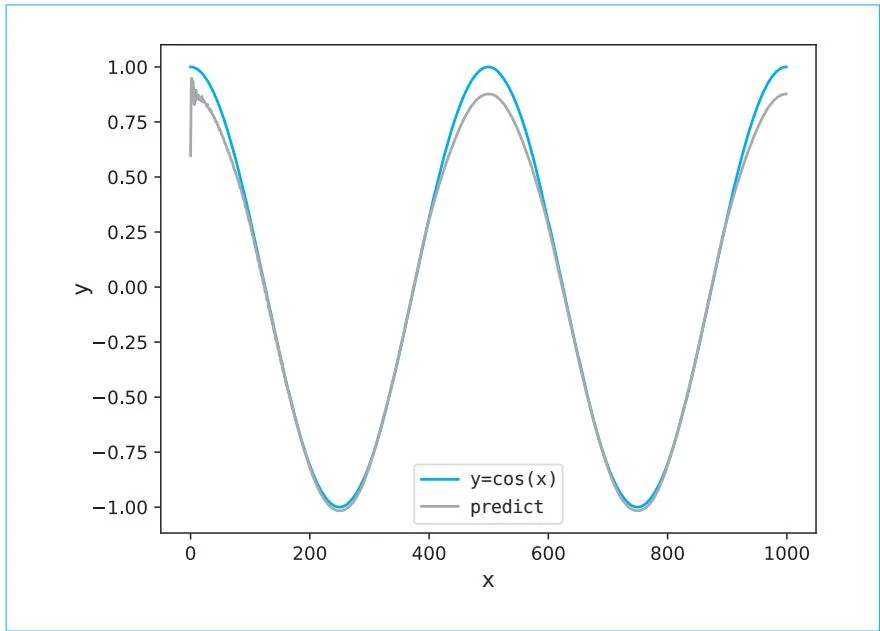
图59-7 模型对新数据的预测结果(y=cos(x))
从图59-7可以看出,预测结果还不错。不过在目前的实现中,数据是一个个处理的(因为批量大小是1),所以处理时间较长。如果增大批量大小,每轮的处理时间将会变短。下一个步骤中我们会修改代码,使数据可以作为小批量数据一次性得到处理,还会使用LSTM层实现更好的模型。
步骤60
LSTM与数据加载器
上一个步骤使用RNN进行了时间序列数据(正弦波)的训练,本步骤将对上一个步骤的代码做两项改进。
第一项改进是编写用于时间序列数据的数据加载器。上一个步骤对一个数据(批量大小为1的数据)进行了模型的正向传播。本步骤将使用针对时间序列数据的数据加载器,对由多个数据组成的小批量数据进行正向传播。
第二项改进是使用LSTM层来代替RNN层。LSTM层的识别精度更高。最后在完成这两项改进之后,我们再次尝试训练正弦波。