28.3_梯度下降法的实现
28.3 梯度下降法的实现
形状复杂的函数,其最大值可能不在梯度指示的方向上(或最小值不在梯度的反方向上)。不过从局部来看,梯度表示函数的输出值最大的方向。重复向梯度方向移动一定距离,然后再次求梯度的过程,可以帮助我们逐渐接近目标位置(最大值或最小值)。这就是梯度下降法。如果从一个好的点开始(给定一个好的初始值),使用梯度下降法就能高效地找到目标值。
下面使用梯度下降法来解决问题。这里的问题是找到Rosenbrock函数
的最小值,因此我们要沿着梯度的反方向前进。考虑到这一点,代码可按下面的方式编写。
steps/step28.py
$\mathbf{x0} =$ Variable(np.array(0.0))
$\mathbf{x1} =$ Variable(np.array(2.0))
lr $= 0.001$ # 学习率
iters $= 1000$ # 迭代次数
for i in range它是:print(x0,x1)
y $=$ rosenbrock(x0,x1)
x0.cleargrad()
x1.cleargrad()
y.backup()
x0.data $- = \text{lr} * \text{x0.deg}$
x1.data $- = \text{lr} * \text{x1.deg}$上面的代码将迭代次数设置为iters。这里的iters是iterations的缩写。与梯度相乘的值是事先设定好的。上面的代码设置了lr=0.001。这里的lr是learning rate的首字母,意思是学习率。

上面代码中的for语句反复使用了Variable实例x0和x1来求导。由于这会使导数值被相继加到x0.gradle和x1.gradle上,所以在计算新的导数时,我们需要重置已经加过其他值的导数。因此,在进行反向传播之前,我们要调用各变量的cleargrad方法来重置导数。
现在运行上面的代码。从输出信息可以看出 的值的更新过程。在终端实际输出的结果如下所示。
运行结果
variable(0.) variable(2.)
variable(0.002) variable(1.6)
variable(0.005276) variable(1.2800008)
...
...
variable(0.68349178) variable(0.4656506)我们可以看到从起点 开始,最小值的位置是如何依次更新的。将计算结果绘制在图上就是图28-2这样。
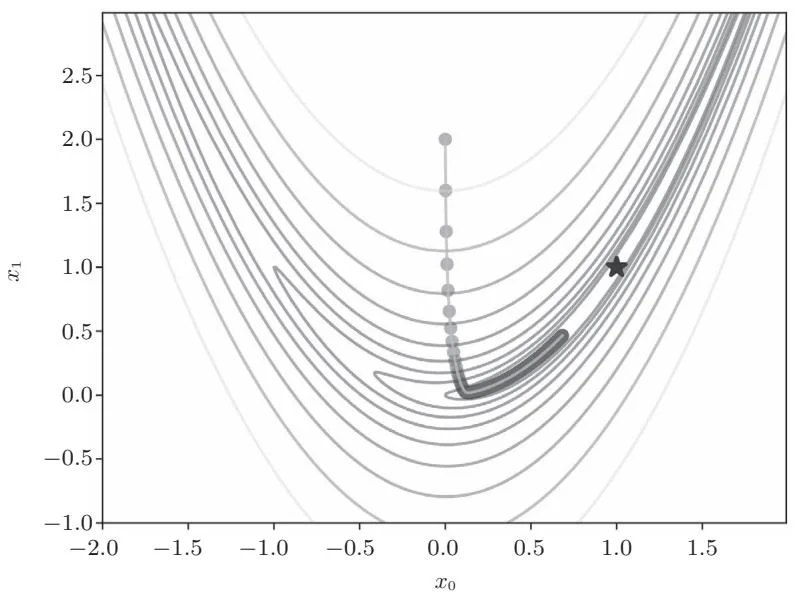
图28-2 更新路径(圆点的轨迹表示更新过程,星号表示最小值的位置)
从图28-2可以看出我们正逐渐接近星号所指的目的地的位置,但尚未到达目的地。所以,我们增加迭代次数,设置iters=10000,结果如图28-3所示。
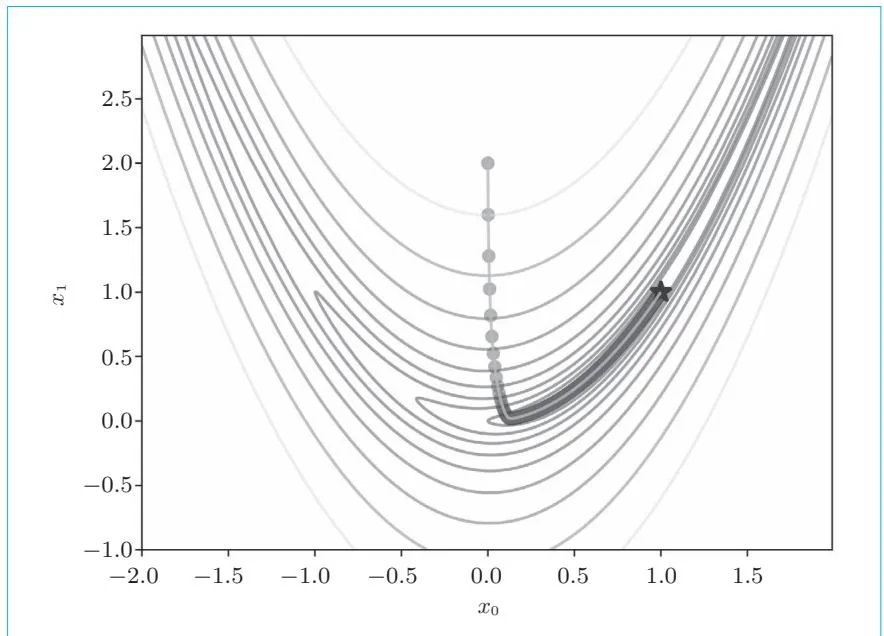
图28-3 iters=10000时的结果
如图28-3所示,这次离目的地更近了。此时 的值为 。如果再增加迭代次数,比如iters=50000,就会抵达 。
本步骤的工作到此结束。在本步骤中,我们使用DeZero实现了梯度下降,找到了Rosenbrock函数的最小值的位置,只是迭代次数实在太多了,有5万次。其实梯度下降法并不擅长处理Rosenbrock这种类型的函数。下一个步骤会介绍并实现另一种优化方法。
步骤29
使用牛顿法进行优化(手动计算)
在上一个步骤中,我们使用梯度下降法求得了Rosenbrock函数的最小值。但在计算过程中,使用梯度下降法要经过近5万次的迭代才能找到梯度。从这个例子可以看出梯度下降法有一个缺点,即在一般情况下,它的收敛速度较慢。
有几种收敛速度较快的方法可用来替代梯度下降法,其中比较有名的是牛顿法。在使用牛顿法进行优化时,我们能以更少的步数获取最优解。以上一个步骤解决的问题为例,我们可以得到如图29-1所示的结果。
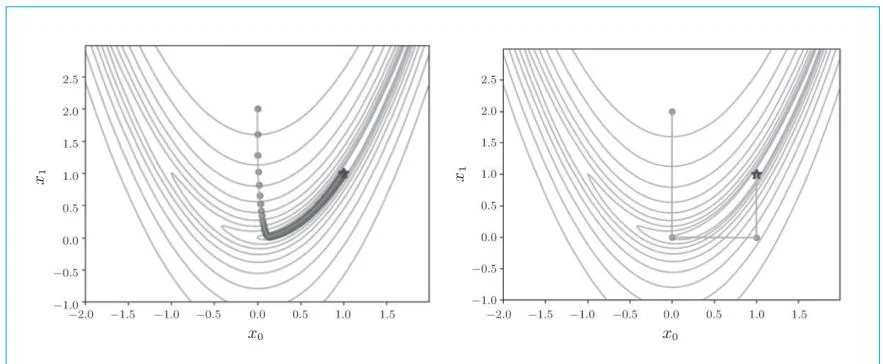
图29-1 采用梯度下降法的更新路径(左图)和采用牛顿法的更新路径(右图)
观察图29-1,可以看到梯度下降法在“山谷”里苦苦寻觅,缓慢地朝着目的地前进,而牛顿法则跳过了“山谷”,一口气到达了目的地。它的迭代
次数仅有6次!梯度下降法需要迭代近5万次,而牛顿法只要6次即可找到目标,二者相差悬殊。

对Rosenbrock函数进行优化时,梯度下降法和牛顿法在迭代次数上有很大的差异。当然因初始值和学习率等设置值的不同,迭代次数也会有很大的变化。在实际问题中,我们一般看不到这么巨大的差异。一般来说,如果初始值与解足够接近,牛顿法会更快收敛。