39.1 sum函数的反向传播

我们已经实现了进行加法运算的函数。当 $y = x_0 + x_1$ 时，加法运算的导数是 $\frac{\partial y}{\partial x_0} = 1$ ， $\frac{\partial y}{\partial x_1} = 1$ 。因此，在反向传播的过程中，从输出端传来的梯度会直接传播到输入端。传播过程如图39-1所示。

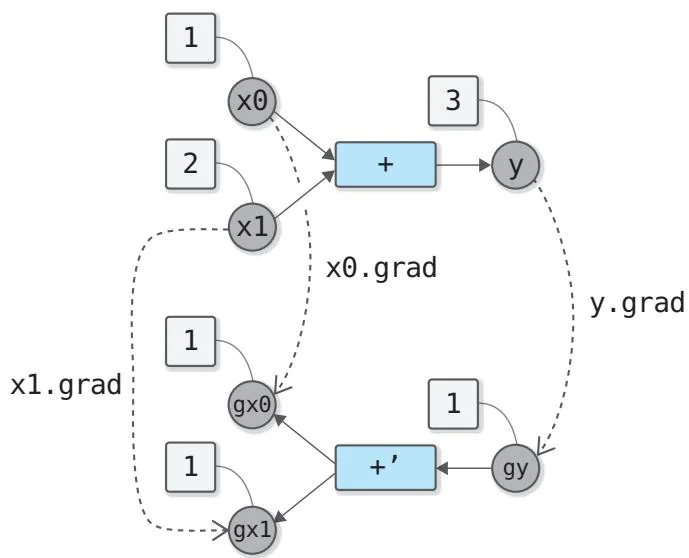
图39-1 加法运算的正向传播和反向传播

从图39-1的计算图可以看出，执行加法运算之后，从变量y开始了反向传播。此时，从输出端传播的梯度值1被复制成两份传给变量 $x0$ 和 $x1$ 。这就是加法运算的反向传播。这种加法运算的反向传播对有两个元素的向量也同样成立。下面请看图39-2。

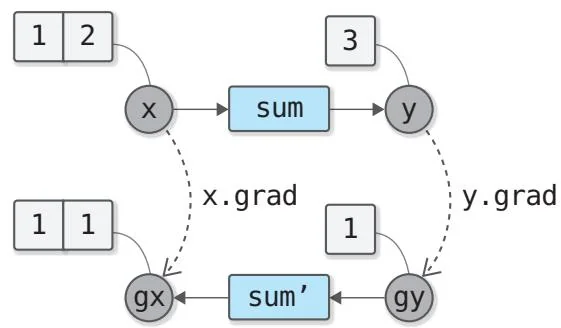
图39-2 sum函数的计算图示例1（用sum'表示执行反向传播的函数）

图39-2中的变量x是一个由两个元素组成的向量。对该向量应用sum函数会输出标量。在反向传播的过程中，从输出端传播的值1被扩展为向量[1, 1]（一维数组）后继续传播。

基于以上内容，我们可以推导出由两个以上元素组成的向量之和的反向传播，关键点就是按向量的元素数量复制梯度。具体如图39-3所示。

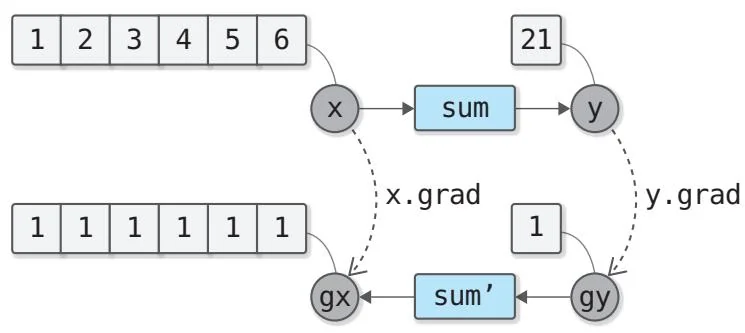
图39-3 sum函数的计算图示例2

如图39-3所示，梯度被复制，其形状与输入变量的形状相同。这就是sum函数的反向传播。它同样适用于输入变量是二维以上数组的情况。下面来实现sum函数。