35.3_高阶导数的计算图可视化
35.3 高阶导数的计算图可视化
在实现了DeZero的tanh函数之后,我们就可以用它来做一些有趣的实验了。具体要做的是计算tanh函数的高阶导数,并将计算图可视化。我们一起去看看随着阶数的增加,计算图会呈现什么样的变化吧。代码如下所示。
steps/step35.py
import numpy as np
fromdezero import Variable
fromdezero.utils import plot.dot_graph
importdezero-functions as F
$\begin{array}{rl} & {\mathbf{x} = \mathrm{Variable}(\mathrm{np.array}(1.0))}\\ & {\mathbf{y} = \mathrm{F.tanh}(\mathbf{x})}\\ & {\mathbf{x.name} = \mathbf{\nabla}^{\prime}\mathbf{x}^{\prime}}\\ & {\mathbf{y.name} = \mathbf{\nabla}^{\prime}\mathbf{y}^{\prime}}\\ & {\mathbf{y-backwardcreate\_graph} = \mathrm{True}} \end{array}$iters $= 0$
for i in range(ifiers): $\mathtt{gx} = \mathtt{x}$ .grad x.cleargrad() gx.backupcreate_graph $\equiv$ True)
#绘制计算图
$\mathtt{gx} = \mathtt{x}$ .grad
gx.name $=$ 'gx' $^+$ str(ifiers+1)
plotDOT_graph(gx,verbose $\equiv$ False,to_file $\equiv$ tanh.png')这段代码与我们之前看到的代码基本相同,都是通过在for语句中重复进行反向传播来求高阶导数的。这里通过iters的值来指定迭代次数:当iters=0时为一阶导数,iters=1时为二阶导数……依此类推,然后将计算图可视化。

在进行计算图的可视化操作时,需要使用步骤26中实现的plot_dodgraph函数。这个函数的实现在dezero/util.py中。
接下来运行上面的代码。首先看一下iters=0时的计算图。结果如图35-2所示。
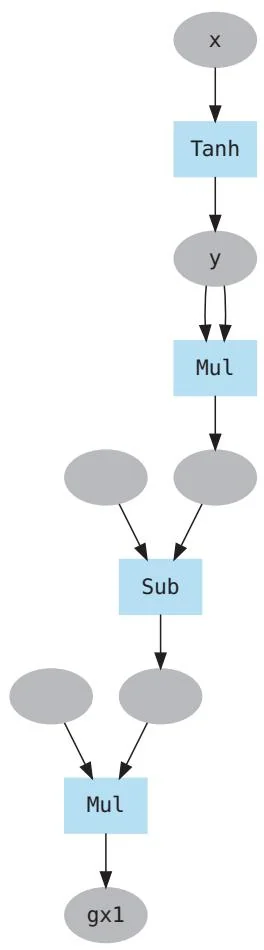
图35-2 的一阶导数的计算图
图35-2是求 的一阶导数的计算图。可以看出图中使用了Tanh、Mul和Sub这些DeZero的函数。接下来改变iters的值,计算二阶导数、三阶导数……由此会产生什么样的计算图呢?结果如图35-3所示。
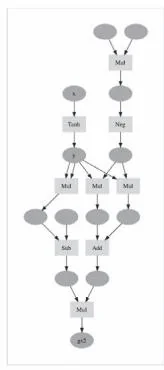
二阶导数
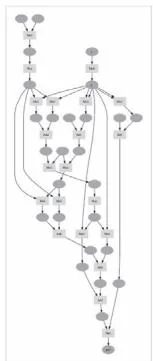
三阶导数
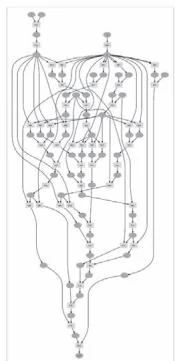
四阶导数
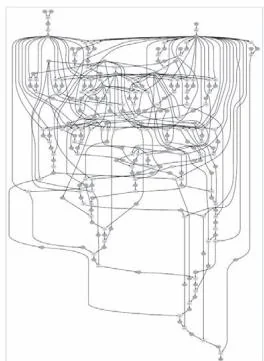
五阶导数
图35-3 阶导数 的计算图
如图35-3所示,随着阶数的增加,计算图的结构也开始变得复杂。通过反向传播,新的计算图在前面计算的基础上被创建,节点的数量因此呈指数增长,我们可以感受到计算图在不断变大。六阶导数和七阶导数的结果如图35-4所示。
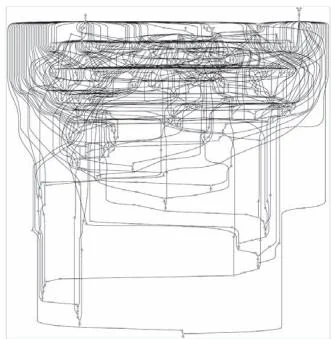
六阶导数
图35-4 阶导数 的计算图
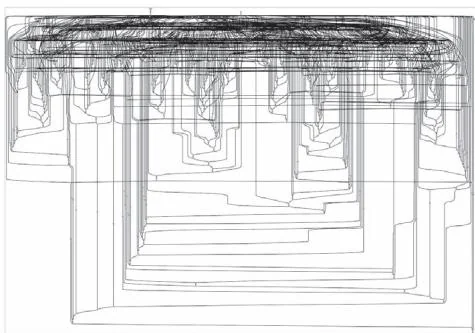
七阶导数
图35-4是相当复杂的计算图,这样复杂的计算图几乎不可能通过人力画出来。DeZero虽然是我们创建的,但它创造出了我们实现不了的东西。从这里我们可以感受到编程的乐趣。
最后以八阶导数为对象进行可视化操作来结束本步骤的内容。结果如图35-5所示。
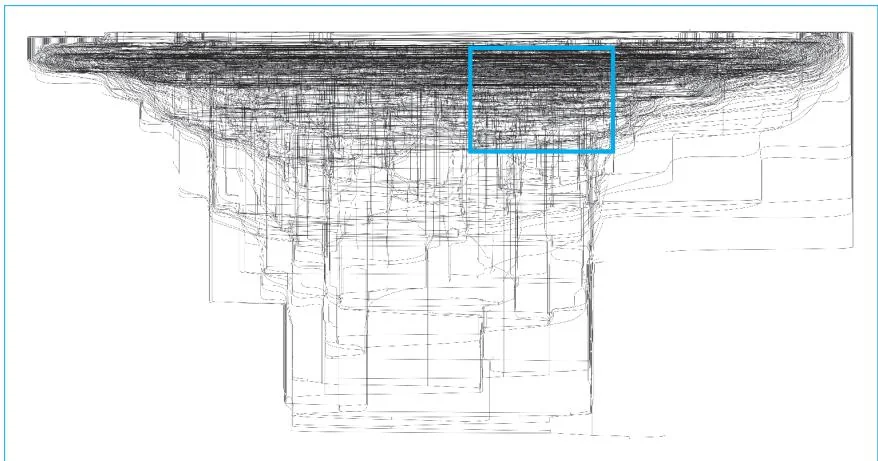
图35-5 八阶导数的计算图
图35-5是一个更为复杂的计算图。我们已经无法在有限的纸面上看清节点的形状了。为了让大家感受到这个计算图有多复杂,下一页放大展示了图35-5方框中的区域。本步骤到此结束。


步骤36
DeZero 的其他用途
前面我们使用了DeZero求高阶导数。其实我们只做了一件事,那就是为反向传播的计算创建连接。其中的重点——为反向传播创建计算图正是DeZero的一个新功能。求高阶导数只不过是DeZero的一个应用示例。本步骤将探索DeZero还有哪些新的用途。

新 DeZero 可以对反向传播进行的计算再次进行反向传播。这个功能叫作 double backpropagation(后面将其称为 double backprop),大多数现代深度学习框架支持这个功能。