29.1 使用牛顿法进行优化的理论知识

本步骤的目标是使用牛顿法实现优化。我们使用牛顿法替代梯度下降法，验证它的确能更快收敛。另外，为了便于说明，我们使用只输入一个变量的函数（Rosenbrock函数要输入两个变量）。

下面推导使用牛顿法进行优化的计算表达式。这里我们思考如何对 $y = f(x)$ 函数求最小值。要推导出计算表达式，首先需要通过泰勒展开将 $y = f(x)$ 变换成如下形式。

通过泰勒展开，我们可以将 $f$ 表示为以某一点 $a$ 为起点的 $x$ 的多项式（关于泰勒展开，笔者已在步骤27中进行了介绍）。在多项式中，一阶导数、二阶导数、三阶导数……各阶导数的项在不断增加，如果我们选择在某一阶结束展开，就可以近似地表示 $f(x)$ 。这里我们选择在二阶导数结束展开。

式子29.2使用到二阶导数为止的项对 $f(x)$ 这个函数进行了近似处理。如果着眼于变量 $x$ ，就可以看出这个表达式是 $x$ 的二次函数。也就是说，“某个函数” $y = f(x)$ 近似为 $x$ 的二次函数。因此，这种近似叫作二次近似。图29-2展示了我们所做的这些工作。

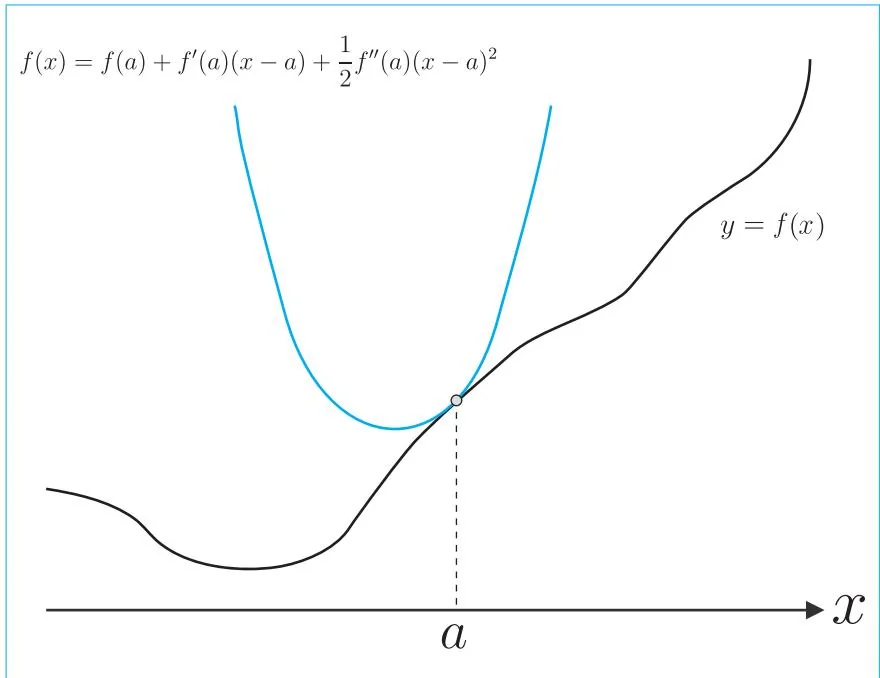
图29-2 以二阶泰勒展开进行近似的示例

如图29-2所示，二次近似函数是一条在点 $a$ 处与 $y = f(x)$ 相交的曲线。让人欣慰的是二次函数的最小值可以通过解析的方式求得。为此，我们要做的就是找到二次函数的导数为0的点。式子如下所示。

从式子29.3可以看出，二次近似函数的最小值位于点 $x = a - \frac{f'(a)}{f''(a)}$ 处。换言之，我们只要将 $a$ 的位置更新为 $-\frac{f'(a)}{f''(a)}$ 即可，如图29-3所示。

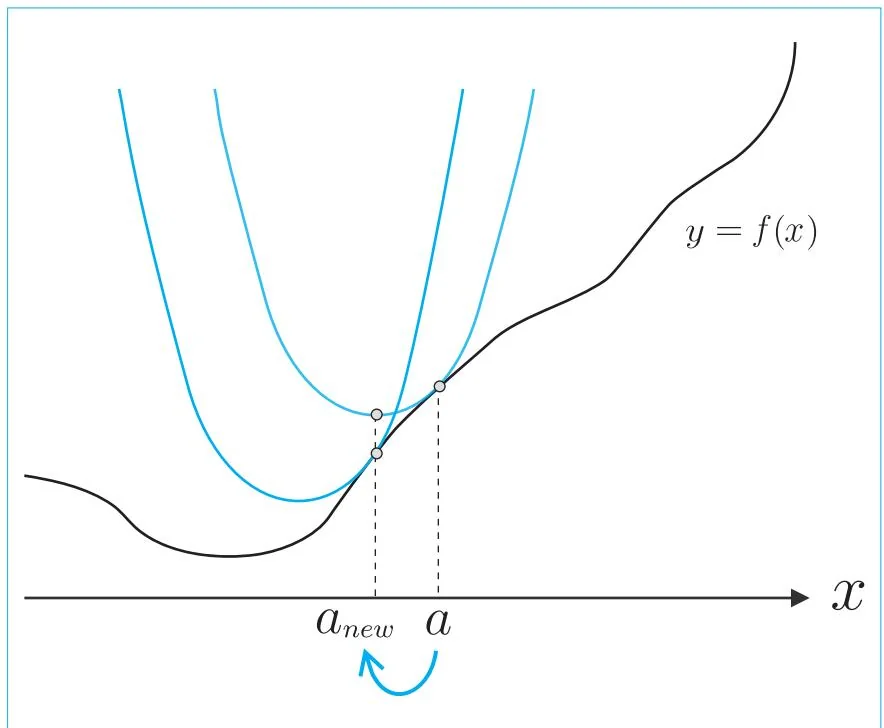
图29-3 更新 $a$ 的位置

将 $a$ 的位置按照图29-3的方式进行更新，在更新后的 $a$ 的位置重复同样的操作。这就是使用牛顿法进行优化的操作。与梯度下降法比较来看的话，牛顿法的特点就更明显了。我们来看下面的式子。

式子29.4为梯度下降法，式子 $29.5$ ① 为牛顿法。从式子可以看出，两种方法都更新了 $x$ ，但更新的方式不同。在梯度下降法中，系数 $\alpha$ 是手动设置

的值， $x$ 的值通过沿着梯度的方向（一阶导数）前进 $\alpha$ 的方式来更新，而牛顿法则通过二阶导数自动调整梯度下降法中的 $\alpha$ 。换言之，我们可以将牛顿法看成 $\alpha = \frac{1}{f''(x)}$ 的方法。

这里探讨的是当函数的输入是标量时的牛顿法。这个理论可以很自然地扩展到函数的输入是向量的情况。不同的是，在向量的情况下要将梯度作为一阶导数，将黑塞矩阵作为二阶导数。详细内容请参考步骤36专栏。

综上所述，梯度下降法只利用一阶导数的信息，而牛顿法还利用了二阶导数的信息。拿物理学中的概念来说就是梯度下降法只使用速度信息，而牛顿法使用速度和加速度的信息。牛顿法有望通过增加的二阶导数的信息来提高搜索效率，从而提高快速到达目的地的概率。

下面使用牛顿法尝试解决一个具体问题——对式子 $y = x^4 - 2x^2$ 执行最小化操作。如图29-4所示，这个函数的图形有两个“凹陷”的地方，取最小值的地方有 $x = -1$ 和 $x = 1$ 两处。这里使用初始值 $x = 2$ ，看看计算能否达到其中一个取最小值的点 $x = 1$ 。

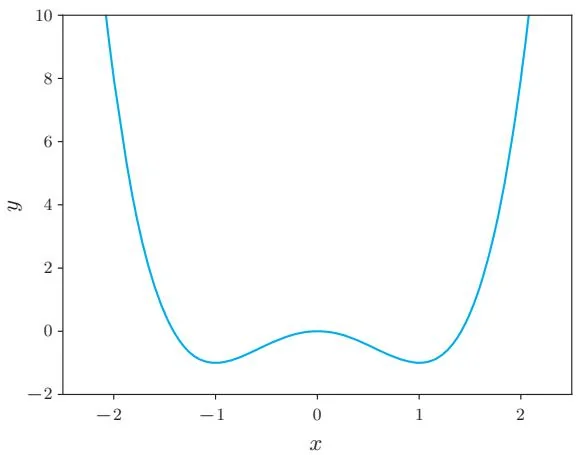
图29-4 $y = x^4 - 2x^2$ 的图形