14.3 重置导数

本步骤要做的唯一修改就是在代码中加上反向传播的导数。不过，我们要注意使用同一个变量进行不同计算的情况。笔者以下面的代码为例进行说明。

第1个计算

$\mathbf{x} =$  Variable(np.array(3.0))   
y  $=$  add(x，x)   
y.backup()   
print(x.grad)

y = add(add(x, x), x)  
y.backup()  
print(x.grad)

2.0
5.0

上面的代码做了2个导数计算。假如为了节省内存要重复使用Variable实例的x，那么在第2次使用x时，x的导数会加在第1次使用x时的导数上。因此，第2次求出的导数5.0是错误的计算结果，正确结果是3.0。

为了解决这个问题，我们要在Variable类中添加一个名为cleargrad的方法来初始化导数。

steps/step14.py

class Variable: def cleargrad(self): self.grad  $=$  None

cleargrad方法用于初始化导数。我们只要在方法中设置self.grad = None即可。这个方法可以帮助我们利用同一个变量求出不同计算的导数。拿前面的例子来说，代码可以写成下面这样。

$\mathbf{x} =$  Variable(np.array(3.0))  
y = add(x, x)  
y.backup()  
print(x.grad) # 2.0

x.cleargrad()  
y = add(add(x, x), x)  
y.backup()  
print(x.grad) # 3.0

2.0
3.0

这次正确求出了第2个计算的导数（第2个计算的导数为3.0，结果正确）。因此，在调用第2个计算的y.backup()之前调用x.cleargrad()，就可以重置变量中保存的导数。这样就可以使用同一个变量来执行其他计算了。

DeZero的cleargrad方法可以用来解决优化问题。优化问题是寻找函数的最小值或最大值的问题。例如，在步骤28中，我们会最小化Rosenbrock函数，届时将使用cleargrad方法。

到这里，本步骤的内容就结束了。通过这个步骤的工作，Variable类进一步得到了提升。不过还有一个重要的问题需要解决。在下一个步骤，我们将解决这个问题。问题解决后，Variable类就完成了。

前面我们处理的都是图15-1这种笔直的计算图。

图15-1 笔直的计算图

然而，变量和函数并不局限于这种简单的连接方式。我们的DeZero已经得到了一定的发展，现在可以创建像图15-2这样的计算图了。

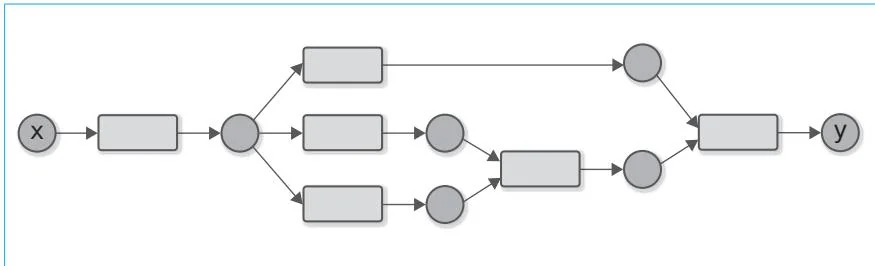
图15-2 更复杂的“连接”的例子

图15-2所示的计算重复使用了同一个变量，也使用了支持多个变量的函数。通过这样的方式，我们可以建立更复杂的“连接”。不过遗憾的是，DeZero不能正确地求出这类计算的导数。准确来说，它无法正确地进行这种复杂“连接”的反向传播。

图的连接方式叫作网络拓扑(topology)。本步骤的目标是支持各种拓扑结构的计算图。我们将引入新的思路，让DeZero不管计算图的连接方式是什么样的，都能正确求导。