55.2 卷积运算

CNN中使用了卷积层。卷积层中执行的处理是卷积运算，它相当于图像处理中的过滤操作。下面笔者以图55-2为例对卷积操作进行说明。

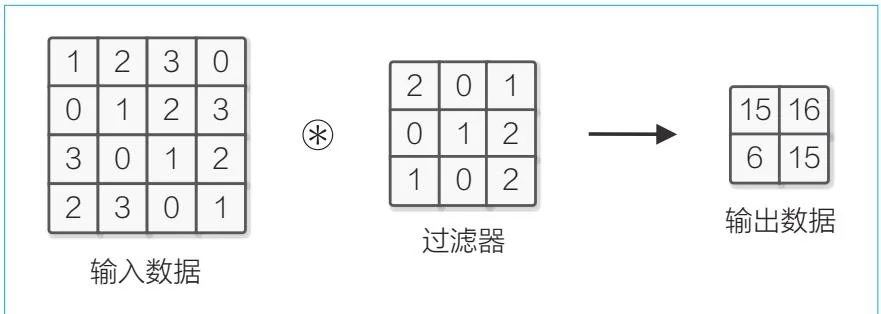
图55-2 卷积运算的例子（卷积运算用 $\text{串}$ 表示）

如图55-2所示，卷积操作对输入数据应用过滤器。在这个例子中，输入数据拥有垂直方向和水平方向这两个维度，过滤器也同样拥有垂直方向和水平方向两个维度。如果按照(width, width)的顺序来描述数据的形状，那么

在这个例子中输入大小为(4，4)，过滤器大小为(3，3)，输出大小为(2，2)。此时的卷积运算会按照图55-3所示的顺序进行。

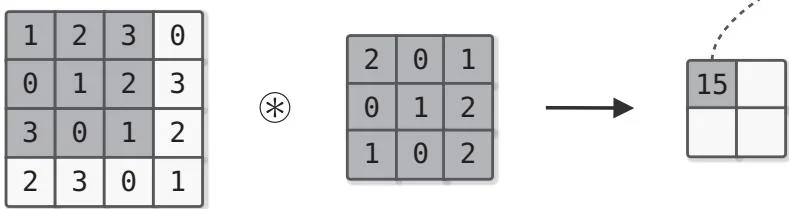
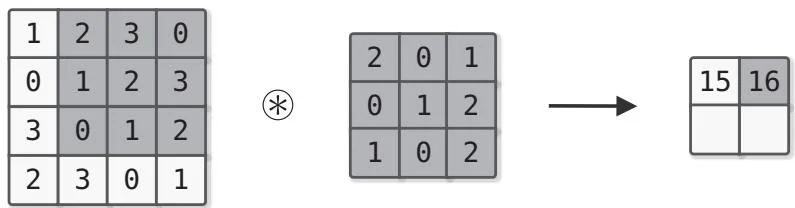
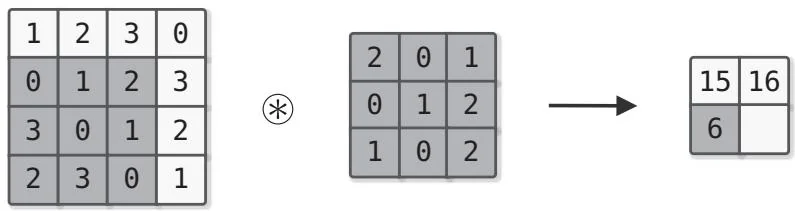
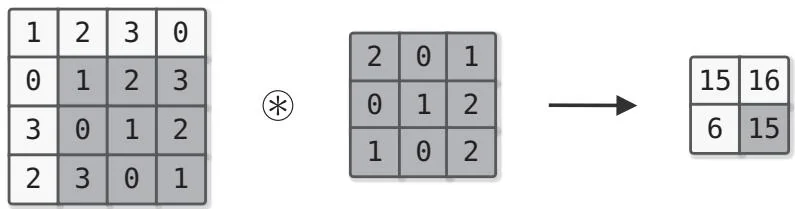
图55-3 卷积运算的计算顺序

卷积运算一边以一定的间隔移动过滤器窗口，一边使用输入数据。如图55-3所示，最终求出的是过滤器和输入的相应元素相乘，然后各项相加的结果。

这个结果会存储在相应的位置。通过对所有位置执行这一过程，可得到卷积运算的输出。另外，这里所说的过滤器在一些资料中用卷积核来表示，本书把过滤器与卷积核看作同一个术语。

仔细观察图55-3中的过滤器，我们会发现它在水平和垂直两个方向上移动。由于这是一个在两个维度上移动的过滤器，所以是二维卷积层。以此类推，如果过滤器只在一个方向移动，就是一维卷积层；如果过滤器在三个方向移动，就是三维卷积层。对于图像，我们主要处理的是二维卷积层。在DeZero中，二维卷积层是以Conv2d这个名字来实现的。

在全连接层的神经网络中，除权重参数之外还有偏置。卷积层也有偏置。包括偏置在内的卷积运算的处理流程如图55-4所示。

图55-4 卷积运算的偏置

如图55-4所示，偏置的加法运算针对的是应用了过滤器之后的数据。请注意，这里只有一个偏置（在这个例子中，应用过滤器之后的数据有4个，偏置只有1个）。在应用过滤器后，该值会加到所有元素中。

接下来介绍卷积层中的填充(padding)和步幅(stride)这两个术语。