42.2 线性回归的理论知识

接下来的目标是找到拟合给定数据的函数。假设 $y$ 和 $x$ 之间的关系是线性的，函数的式子就可以表示为 $y = Wx + b$ （其中 $W$ 是标量）。 $y = Wx + b$ 这条直线如图42-2所示。

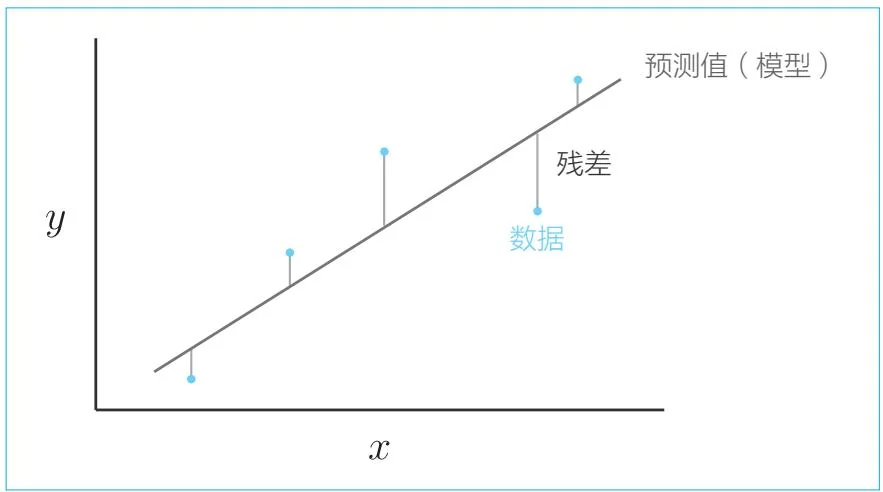
图42-2 线性回归的示例

如图42-2所示，我们的目标是找到一条拟合数据的直线 $y = Wx + b$ 。为此，我们需要尽可能地减小数据和预测值之间的差，这个差叫作残差(residual)。下面是表示预测值(模型)和数据之间的误差指标的式子。

在式子42.1中，先求出这 $N$ 个点中的每个点 $(x_{i},y_{i})$ 的平方误差，然后将它们加起来，之后乘以 $\frac{1}{N}$ 求出平均数。这个式子叫作均方误差（mean squared error）。另外，在式子42.1中求平均数时乘的是 $\frac{1}{N}$ ，但在某些情况下，会乘以 $\frac{1}{2N}$ 。但无论哪种情况，在用梯度下降法求解时，都可以通过调整学习率的值来解决同样的问题。

评估模型好坏的函数叫作损失函数(loss function)。此时，我们可以说线性回归使用均方误差作为损失函数。

我们的目标是找到使式子42.1表示的损失函数的输出最小的 $W$ 和 $b$ 。这就是函数优化问题。我们已经(在步骤28中)用梯度下降法解决了这样的问题。此处同样使用梯度下降法来找到使式子42.1最小化的参数。