0x45点分治

到目前为止，我们用数据结构处理的大多是序列上的问题。这些问题的形式一般是给定序列中的两个位置 $l$ 和 $r$ ，在区间 $[l, r]$ 上执行查询或修改指令。如果给定一棵树，以及树上两个节点 $x$ 和 $y$ ，那么与“序列上的区间”相对应的就是“树上两点之间的路径”。我们先不考虑对路径进行修改的操作。本节中介绍的点分治就是在一棵树上，对具有某些限定条件的路径静态地进行统计的算法。

【例题】Tree FOJ1741

给一棵有 $N$ 个点的树，每条边都有一个权值。树上两个节点 $x$ 与 $y$ 之间的路径长度就是路径上各条边的权值之和。求长度不超过 $K$ 的路径有多少条。

本题树中的边是无向的，即这棵树是一个由 $N$ 个点、 $N - 1$ 条边构成的无向连通图。我们把这种树称为“无根树”，也就是说可以任意指定一个节点为根节点，而不影响问题的答案。

若指定节点 $p$ 为根，则对 $p$ 而言，树上的路径可以分为两类：

1. 经过根节点 $p$ 。

2. 包含于 $p$ 的某一棵子树中（不经过根节点）。

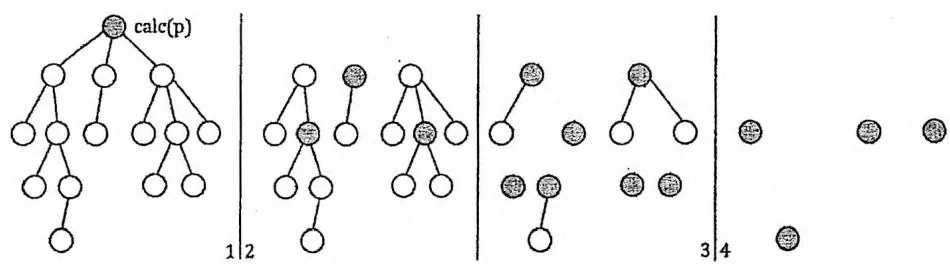
根据分治的思想，对于第2类路径，显然可以把 $p$ 的每棵子树作为子问题，递归进行处理。

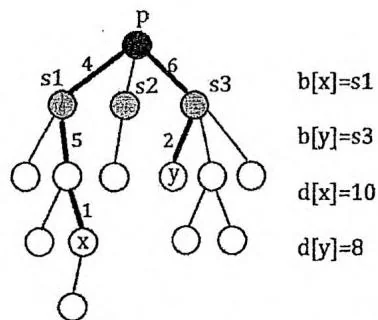
而对于第1类路径，可以从根节点 $p$ 分成“ $x \sim p$ ”与“ $p \sim y$ ”两段。回顾在0x21节所学的知识，我们可以从 $p$ 出发对整棵树进行DFS，求出数组 $d$ ，其中 $d[x]$ 表示点 $x$ 到根节点 $p$ 的距离。同时还可以求出数组 $b$ ，其中 $b[x]$ 表示点 $x$ 属于根节点 $p$ 的哪一棵子树，特别地，令 $b[p] = p$ 。

此时满足题目要求的第1类路径就是满足以下两个条件的点对 $(x,y)$ 的个数：

1. $b[x]\neq b[y]_{\circ}$

2. $d[x] + d[\gamma ]\leq K$

如下图所示。

定义 $Calc(p)$ 表示在以 $p$ 为根的树中统计上述点对的个数（第1类路径的条数）。 $Calc(p)$ 有两种常见的实现方式。针对不同的题目，二者各有优劣。

方法一：树上直接统计

设 $p$ 的子树为 $s_1, s_2, \dots, s_m$ 。

对于 $s_i$ 中的每个节点 $x$ ，把在子树 $s_1, s_2, \dots, s_{i-1}$ 中的满足 $d[x] + d[y] \leq K$ 的节点 $y$ 的个数累加到答案中即可。

具体来说，可以建立一个树状数组，依次处理每棵子树 $s_i$ 。

1. 对 $s_i$ 中的每个节点 $x$ ，查询前缀和 $\operatorname{ask}(K - d[x])$ ，即为所求的 $y$ 的个数。

2. 对 $s_i$ 中的每个节点 $x$ , 执行 $\operatorname{add}(d[x], 1)$ , 表示与 $p$ 距离为 $d[x]$ 的节点增加了 1 个。

按子树一棵棵进行处理保证了 $b[x] \neq b[y]$ ，查询前缀和保证了 $d[x] + d[y] \leq K$ 。

需要注意的是，树状数组的范围与路径长度有关，这个范围远比 $N$ 要大。而本题中不易进行离散化。一种解决方案是用平衡树代替树状数组，以保证 $O(N \log N)$ 的复杂度，但代码复杂程度显著增加。所以本题更适用下一种方法。

方法二：指针扫描数组

把树中每个点放进一个数组 $a$ ，并把数组 $a$ 按照节点的 $d$ 值排序。

使用两个指针 $L, R$ 分别从前、后开始扫描 $a$ 数组。

容易发现，在指针 $L$ 从左向右扫描的过程中，恰好使得 $d[a[L]] + d[a[R]] \leq K$ 的指针 $R$ 的范围是从右向左单调递减的。

另外，我们用数组 $cnt[s]$ 维护在 $L + 1$ 与 $R$ 之间满足 $b[a[i]] = s$ 的位置 $i$ 的个数。

于是，当路径的一端 $x$ 等于 $a[L]$ 时，满足题目要求的路径另一端 $y$ 的个数就是 $R - L - cnt[b[a[L]]]$ 。

总而言之，整个点分治算法的过程就是：

1. 任选一个根节点 $p$ （后面我们将说明， $p$ 应该取树的重心）。

2. 从 $p$ 出发进行一次 DFS，求出 $d$ 数组和 $b$ 数组。

3. 执行 $\text{Calc}(p)$ 。

4. 删除根节点 $p$ ，对 $p$ 的每棵子树（看作无根树）递归执行 1~4 步。

在点分治过程中，每一层的所有递归过程合计对每个节点处理1次。因此，若递归最深到达第 $T$ 层，则整个算法的时间复杂度就是 $O(TN\log N)$ 。

如果问题中的树是一条链，最坏情况下每次都以链的一端为根，那么点分治将需要递归 $N$ 层，时间复杂度退化到 $\mathrm{O}(N^2\log N)$ 。为了避免这种情况，我们每次选择树的重心（曾在0x21节中提及）作为根节点 $p$ 。此时容易证明 $p$ 的每棵子树的大小都不会超过整棵树大小的一半，点分治就至多递归 $\mathrm{O}(\log N)$ 层，整个算法的时间复杂度为 $\mathrm{O}(N\log^2 N)$ 。如下图所示。