0x16 Trie

Trie，又称字典树，是一种用于实现字符串快速检索的多叉树结构。Trie 的每个节点都拥有若干个字符指针，若在插入或检索字符串时扫描到一个字符 $c$ ，就沿着当前节点的 $c$ 这个字符指针，走向该指针指向的节点。下面我们来详细讨论 Trie 的基本操作过程。

初始化

一棵空Trie仅包含一个根节点，该点的字符指针均指向空。

插入

当需要插入一个字符串 $S$ 时，我们令一个指针 $P$ 起初指向根节点。然后，依次扫描 $S$ 中的每个字符 $c$ ：

1. 若 $P$ 的 $c$ 字符指针指向一个已经存在的节点 $Q$ ，则令 $P = Q$ 。

2. 若 $P$ 的 $c$ 字符指针指向空，则新建一个节点 $Q$ ，令 $P$ 的 $c$ 字符指针指向 $Q$ ，然后令 $P = Q$ 。

当 $S$ 中的字符扫描完毕时，在当前节点 $P$ 上标记它是一个字符串的末尾。

检索

当需要检索一个字符串 $S$ 在Trie中是否存在时，我们令一个指针 $P$ 起初指向根节点，然后依次扫描 $S$ 中的每个字符 $c$

1. 若 $P$ 的 $c$ 字符指针指向空，则说明 $S$ 没有被插入过Trie，结束检索。

2. 若 $P$ 的 $c$ 字符指针指向一个已经存在的节点 $Q$ ，则令 $P = Q$ 。

当 $S$ 中的字符扫描完毕时，若当前节点 $P$ 被标记为一个字符串的末尾，则说明 $S$ 在Trie中存在，否则说明 $S$ 没有被插入过Trie。

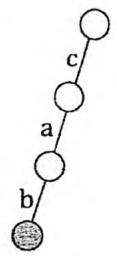
在空Trie中插入cab

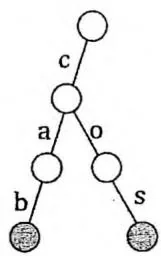
继续插入cos

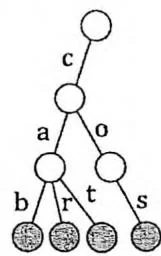
继续插入car与cat

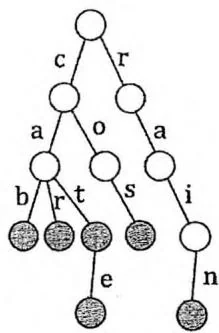
继续插入 cate与rain

在上图所示的例子中，需要插入和检索的字符串都由小写字母构成，所以Trie的

每个节点具有26个字符指针，分别为a到z。上图展示了在一棵空Trie中依次插入“cab”“cos”“car”“cat”“cate”和“rain”后的Trie的形态，灰色标记了单词的末尾节点。可以看出在Trie中，字符数据都体现在树的边（指针）上，树的节点仅保存一些额外信息，例如单词结尾标记等。其空间复杂度是 $O(NC)$ ，其中 $N$ 是节点个数， $C$ 是字符集的大小。

int trie[SIZE][26],tot  $= 1$  //初始化，假设字符串由小写字母构成  
void insert(char\*str）{//插入一个字符串intlen  $\equiv$  strlen(str)，p  $= 1$  ·for（intk  $= 0$  ;k<len;k++）{int ch  $\equiv$  str[k]-'a';if(trie[p][ch]  $\equiv = 0$  )trie[p][ch]  $\equiv + +$  tot;  $\mathsf{p} =$  trie[p][ch];}end[p]  $\equiv$  true;  
}  
bool search(char\*str）{//检索字符串是否存在intlen  $\equiv$  strlen(str)，p  $= 1$  ·for（intk  $= 0$  ;k<len;k++）{p  $\equiv$  trie[p][str[k]-'a'];if(p  $\equiv = 0$  )return false;1return end[p];

【例题】前缀统计

给定 $N$ 个字符串 $S_{1}, S_{2}, \dots, S_{N}$ 。接下来进行 $M$ 次询问，每次询问给定一个字符串 $T$ ，求 $S_{1} \sim S_{N}$ 中有多少个字符串是 $T$ 的前缀。输入字符串的总长度不超过 $10^{6}$ 。

把这 $N$ 个字符串插入一棵Trie树，Trie树的每个节点上存储一个整数cnt，记录该节点是多少个字符串的末尾节点。（为了处理插入重复字符串的情况，这里要记录个数，而不能只做结尾标记）

对于每个询问，在Trie树中检索 $T$ ，在检索过程中累加途径的每个节点的cnt值，就是该询问的答案。

【例题】TheXORLargestPair

在给定的 $N$ 个整数 $A_{1}, A_{2}, \dots, A_{N}$ 中选出两个进行 $\mathrm{xor}$ （异或）运算，得到的结果

最大是多少？ $N\leq 10^{5},0\leq A_{l} < 2^{31}$

我们考虑所有的二元组 $(i,j)$ 且 $i < j$ ，那么本题的目标就是在其中找到 $A_{i}$ xor $A_{j}$ 的最大值。也就是说，对于每个 $i(1 \leq i \leq N)$ ，我们希望找到一个 $j(1 \leq j < i)$ ，使 $A_{i}$ xor $A_{j}$ 最大，并求出这个最大值。

我们可以把每个整数看作长度为32的二进制01串（数值较小时在前边补0），并且把 $A_{1} \sim A_{i-1}$ 对应的32位二进制串插入一棵Trie树（最低二进制位为叶子节点）。接下来，对于 $A_{i}$ 对应的32位二进制串，我们在Trie中进行一次与检索类似的过程，每一步都尝试沿着“与 $A_{i}$ 的当前位相反的字符指针”向下访问。若“与 $A_{i}$ 的当前位相反的字符指针”指向空节点，则只好访问与 $A_{i}$ 当前位相同的字符指针。根据xor运算“相同得0，不同得1”的性质，该方法即可找出与 $A_{i}$ 做xor运算结果最大的 $A_{j}$ 。

如下图所示，在一棵插入了2(010)，5(101)，7(111）三个数的Trie中，分别查询与6(110)，3(011)做xor运算结果最大的数。（为了简便，图中使用了3位二进制数代替32位二进制数）

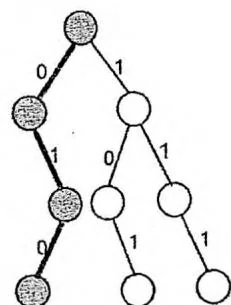
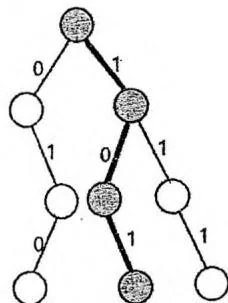
查询与110做xor运算结果最大的数，查询与011做xor运算结果最大的数

综上所述，我们可以循环 $i = 1\sim N$ ，对于每个 $i$ ，Trie 树中应该存储了 $A_{1}\sim A_{i - 1}$ 对应的32位二进制串。（实际上每次 $i$ 增长前，把 $A_{i}$ 插入Trie即可）根据我们刚才提到的“尽量走相反的字符指针”的检索策略，就可以找到所求的 $A_{j}$ ，更新答案。

【例题】The XOR Longest Path FOJ3764

给定一棵 $N$ 个节点的树，树上的每条边都有一个权值。从树中选择两个点 $x$ 和 $y$ ，把从 $x$ 到 $y$ 的路径上的所有边权 $\mathrm{xor}$ （异或）起来，得到的结果最大是多少？ $N \leq 10^5$ 。

设 $D[x]$ 表示根节点到 $\pmb{x}$ 的路径上所有边权的xor值，显然有：

根据上式，我们可以对树进行一次深度优先遍历，求出所有的 $D[x]$ 。不难发现，树上 $x$ 到 $y$ 的路径上所有边权的 $\mathbf{xor}$ 结果就等于 $D[x] \text{xor } D[y]$ 。这是因为根据 $\mathbf{xor}$

运算的性质（ $a \text{ xor } a = 0$ ），“ $x$ 到根”和“ $y$ 到根”这两条路径重叠的部分恰好抵消掉。

所以，问题就变成了从 $D[1] \sim D[N]$ 这 $N$ 个数中选出两个，xor的结果最大，即上一道例题。可以用Trie树来快速求解。

$0 \times 17$ 二叉堆

二叉堆是一种支持插入、删除、查询最值的数据结构。它其实是一棵满足“堆性质”的完全二叉树①，树上的每个节点带有一个权值。若树中的任意一个节点的权值都小于等于其父节点的权值，则称该二叉树满足“大根堆性质”。若树中任意一个节点的权值都大于等于其父节点的权值，则称该二叉树满足“小根堆性质”。满足“大根堆性质”的完全二叉树就是“大根堆”，而满足“小根堆性质”的完全二叉树就是“小根堆”，二者都是二叉堆的形态之一。

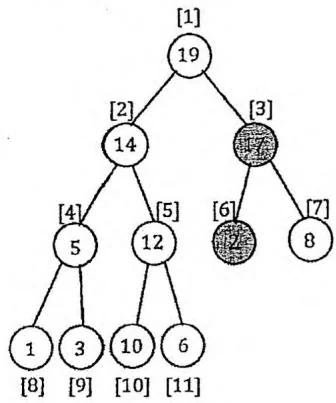
根据完全二叉树的性质，我们可以采用层次序列存储方式，直接用一个数组来保存二叉堆。层次序列存储方式，就是逐层从左到右为树中的节点依次编号，把此编号作为节点在数组中存储的位置（下标）。在这种存储方式中，父节点编号等于子节点编号除以2，左子节点编号等于父节点编号乘2，右子节点编号等于父节点编号乘2加1，如下图所示。

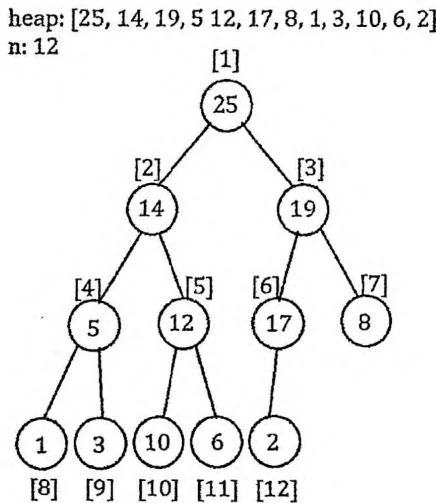
我们以大根堆为例探讨堆支持的几种常见操作的实现。

Insert

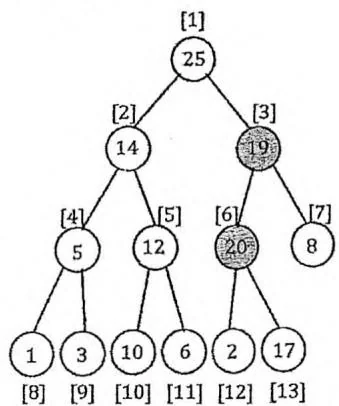
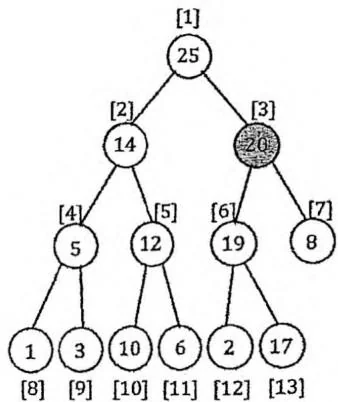
Insert(val) 操作向二叉堆中插入一个带有权值 val 的新节点。我们把这个新节点直接放在存储二叉堆的数组末尾，然后通过交换的方式向上调整，直至满足堆性质。其时间复杂度为堆的深度，即 $O(\log N)$ 。

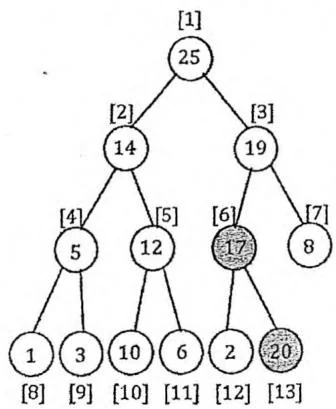
int heap[SIZE], n;  
void up(int p) { // 向上调整  
    while (p > 1) {  
        if (heap[p] > heap[p/2]) { // 子节点>父节点，不满足大根堆性质  
            swap(heap[p], heap[p/2]);  
            p /= 2;  
        }  
    else break;  
}  
}  
void Insert(int val) {  
    heap[++n] = val;  
    up(n);  
}

GetTop

GetTop 操作返回二叉堆的堆顶权值，即最大值 heap[1]，复杂度为 0(1)。

int GetTop(){ return heap[1]; }

Extract

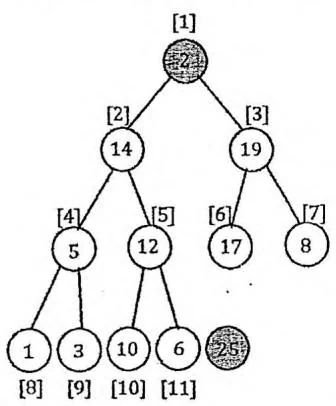
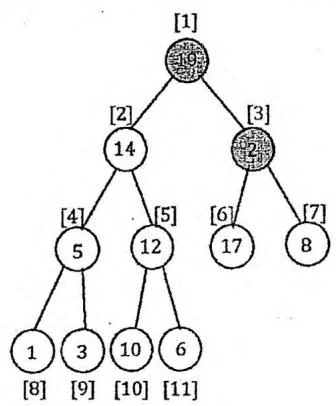
Extract 操作把堆顶从二叉堆中移除。我们把堆顶 heap[1] 与存储在数组末尾的

节点 $heap[n]$ 交换，然后移除数组末尾节点（令 $n$ 减小1），最后把堆顶通过交换的方式向下调整，直至满足堆性质。其时间复杂度为堆的深度，即 $O(\log N)$ 。

void down(int p) { int s = p*2; // p的左子节点 while (s <= n) { if (s<n && heap[s]<heap[s+1]) s++; // 左右子节点中取较大者 if (heap[s]>heap[p]) { // 子节点大于父节点，不满足大根堆性质 swap(heap[s], heap[p]); p = s, s = p*2; } else break; }   
}   
void Extract() { heap[1] = heap[n--]; down(1);

Remove

Remove(p) 操作把存储在数组下标 $p$ 位置的节点从二叉堆中删除。与 Extract 相类似，我们先把 heap[p] 与 heap[n] 交换，然后令 $n$ 减小 1。注意此时 heap[p] 既有可能需要向下调整，也有可能需要向上调整，需要分别进行检查和处理。时间复杂度为 $O(\log N)$ 。

void Remove(int k) { heap[k] = heap[n--]; up(k), down(k); }

C++ STL 中的 priority_queue(优先队列)为实现了一个大根堆, 支持 push Insert), top(GetTop) 和 pop Extract) 操作, 不支持 Remove 操作, 详细用法参见第 0x71 节。

【例题】Supermarket POJ1456

给定 $N$ 个商品，每个商品有利润 $p_i$ 和过期时间 $d_i$ ，每天只能卖一个商品，过期商品不能再卖，求如何安排每天卖的商品，可以使收益最大。 $1 \leq N, p_i, d_i \leq 10^4$ 。

容易想到一个贪心策略：在最优解中，对于每个时间（天数） $t$ ，应该在保证不卖出过期商品的前提下，尽量卖出利润前 $t$ 大的商品。因此，我们可以依次考虑每个商品，动态维护一个满足上述性质的方案。

详细地说，我们把商品按照过期时间排序，建立一个初始为空的小根堆（节点权值为商品利润），然后扫描每个商品：

1. 若当前商品的过期时间（天数） $t$ 等于当前堆中的商品个数，说明在目前方案下，前 $t$ 天已经安排了 $t$ 个商品卖出。此时，若当前商品的利润大于堆顶权值（即已经安排的 $t$ 个商品中的最低利润），则替换掉堆顶（用当前商品替换掉原方案中利润最低的商品）。

2. 若当前商品的过期时间（天数）小于当前堆中的商品个数，直接把该商品插入堆。

最终，堆里的所有商品就是我们需要卖出的商品，它们的利润之和就是答案。该算法的时间复杂度为 $O(N \log N)$ 。

【例题】Sequence POJ2442

给定 $M$ 个长度为 $N$ 的序列，从每个序列中任取一个数求和，可以构成 $N^M$ 个和，求其中最小的 $N$ 个和。 $N \leq 2000, M \leq 100$ 。

先来考虑当 $M = 2$ 时的简化问题，即从2个序列中任取一个数相加构成的 $N^2$ 个和中求出前 $N$ 小的和。设这两个序列为 $A$ 和 $B$ ，把它们分别排序。

可以发现，最小和一定是 $A[1] + B[1]$ ，次小和是 $\min(A[1] + B[2], A[2] + B[1])$ 。假设次小和是 $A[2] + B[1]$ ，那么第3小和就是 $A[1] + B[2]$ ， $A[2] + B[2]$ ， $A[3] + B[1]$ 三者之一。也就是说，当确定 $A[i] + B[j]$ 为第 $k$ 小和后， $A[i + 1] + B[j]$ 与 $A[i] + B[j + 1]$ 就加入了第 $k + 1$ 小和的备选答案集合。读者可以类比有两个指针分别指向 $A[i]$ 和 $B[j]$ ，把其中一个指针向后移动一位，就可能产生下一个和。

需要注意的是， $A[1] + B[2]$ 与 $A[2] + B[1]$ 都能产生 $A[2] + B[2]$ 这个备选答案。为了避免重复，我们可以规定：如果把 $j$ 加 1 产生新的备选答案，那么以后只能再增加 $j$ ，不能再增加 $i$ 。也就是说，从 $A[1] + B[1]$ 到任何 $A[i] + B[j]$ 必须先向后移动

指向 $A$ 的指针 $i$ ，再向后移动指向 $B$ 的指针 $j$ ，这样就可以保证备选答案产生路线的唯一性。

我们建立一个小根堆，堆中每个节点存储一个三元组 $(i,j,last)$ ，其中last表示上一次移动的指针是不是 $j$ ，堆的比较操作以 $A[i] + B[j]$ 作为节点权值。

起初，堆中只有(1,1,false)。

取出堆顶 $(i,j,last)$ , 然后把 $(i,j + 1,\text{true})$ 插入堆, 如果 last 为 false, 再把 $(i + 1,j,\text{false})$ 也插入堆。

重复上一步 $N$ 次，每次取出的堆顶节点的权值 $A[i] + B[j]$ 一起构成前 $N$ 小和。该算法的时间复杂度为 $O(N \log N)$ 。

回到本题，根据数学归纳法，我们可以先求出前2个序列中任取一个数相加构成的前 $N$ 小和，把这 $N$ 个和作为一个序列，再与第3个序列求新的前 $N$ 小和，依此类推，最终得到 $M$ 个序列任取一个数相加构成的前 $N$ 小和。整个算法的时间复杂度为 $\mathsf{O}(MN\log N)$

【例题】数据备份 CTSC2007/BZOJ1150

你在一家IT公司为大型写字楼或办公楼（offices）的计算机数据做备份。然而数据备份的工作是枯燥乏味的，因此你想设计一个系统让不同的办公楼彼此之间互相备份，而你则坐在家中尽享计算机游戏的乐趣。

已知办公楼都位于同一条街上。你决定给这些办公楼配对（两个一组）。每一对办公楼可以通过在这两个建筑物之间铺设网络电缆使得它们可以互相备份。然而，网络电缆的费用很高。当地电信公司仅能为你提供 $K$ 条网络电缆，这意味着你仅能为 $K$ 对办公楼（或总计 $2K$ 个办公楼）安排备份。任一个办公楼都属于唯一的配对组（换句话说，这 $2K$ 个办公楼一定是相异的）。此外，电信公司需按网络电缆的长度（公里数）收费。因而，你需要选择这 $K$ 对办公楼使得电缆的总长度尽可能短。换句话说，你需要选择这 $K$ 对办公楼，使得每一对办公楼之间的距离之和（总距离）尽可能小。

下面给出一个示例，假定你有5个客户，其办公楼都在一条街上，如下图所示。这5个办公楼分别位于距离大街起点 $1\mathrm{km}, 3\mathrm{km}, 4\mathrm{km}, 6\mathrm{km}$ 和 $12\mathrm{km}$ 处。电信公司仅为你提供 $K = 2$ 条电缆。

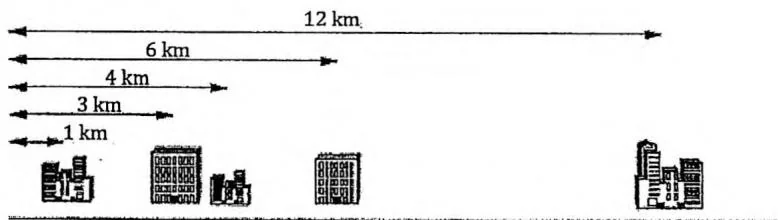
上例最好的配对方案是将第1个和第2个办公楼相连，第3个和第4个办公楼相连。这样可按要求使用 $K = 2$ 条电缆。第1条电缆的长度是 $3\mathrm{km} - 1\mathrm{km} = 2\mathrm{km}$ ，第2条电缆的长度是 $6\mathrm{km} - 4\mathrm{km} = 2\mathrm{km}$ 。这种配对方案需要总长 $4\mathrm{km}$ 的网络电缆，满足距离之和最小的要求。

办公楼数目 $N$ 满足 $2 \leq N \leq 10^{5}$ ，电缆数 $K$ 满足 $1 \leq K \leq N / 2$ 。

我们很容易发现，最优解中每两个配对的办公楼一定是相邻的。我们求出每两个相邻办公楼之间的距离，记为 $D_{1}, D_{2}, D_{3}, \dots, D_{N-1}$ 。于是问题可以转化为：从数列 $D$ 中选出不超过 $K$ 个数（对应办公楼的 $K$ 个配对），使它们的和最小，并且相邻的两个数不能同时被选（任一办公楼都属于唯一的配对组）。

如果 $K = 1$ ，答案显然是 $D$ 数列中的最小值。

如果 $K = 2$ ，答案一定是以下两种情况之一：

1. 选择最小值 $D_{i}$ ，以及除了 $D_{i-1}, D_{i}, D_{i+1}$ 之外其他数中的最小值。

2. 选择最小值 $D_{i}$ 左右两侧的两个数，即 $D_{i-1}$ 和 $D_{i+1}$ 。

这很容易证明：如果 $D_{i-1}$ 和 $D_{i+1}$ 都没有选，那么不选最小值 $D_i$ 一定不优；如果 $D_{i-1}$ 和 $D_{i+1}$ 选了一个，那么把选了的那个换成 $D_i$ ，答案也会变小，所以最优解必定是上面两种情况之一。

通过上述证明，我们也可以得到一个推论：在最优解中，最小值左右两侧的数要么同时选，要么都不选。

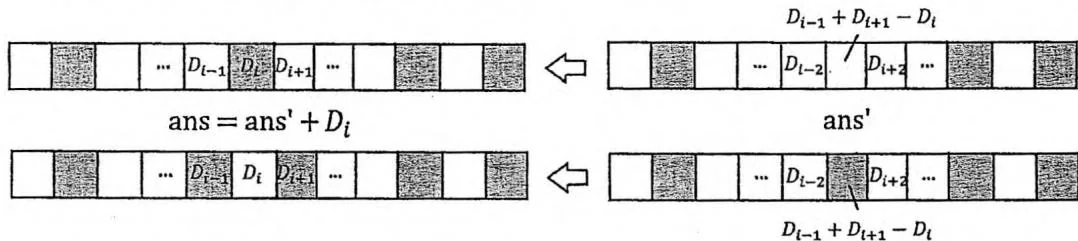
因此，我们可以先选上 $D$ 数列中的最小值，然后把 $D_{i-1}, D_i, D_{i+1}$ 从 $D$ 数列中删除，把 $D_{i-1} + D_{i+1} - D_i$ 插入到 $D$ 数列中刚才执行删除的位置。最后，求解“从新的 $D$ 数列中选出不超过 $K-1$ 个数，使它们的和最小，并且相邻两个数不能同时被选”这个子问题。

在这个子问题中，如果选了 $D_{i-1} + D_{i+1} - D_i$ 这个数，相当于去掉 $D_i$ ，换上 $D_{i-1}$ 和 $D_{i+1}$ ；如果没选，那么刚才选择最小值 $D_i$ 显然是一步最优策略。这恰好涵盖了我们在推论中提到的最优解当中的两种情况。

综上所述，我们得到了一个这样的算法：

建立一个链表 $L$ ，连接 $N - 1$ 个节点，节点上分别记录数值 $D_{1},D_{2},D_{3},\dots ,D_{N - 1}$

即每两个相邻办公楼之间的距离。再建立一个小根堆，与链表构成映射关系（就是说堆中也有 $N - 1$ 个节点，节点权值分别是 $D_{1}, D_{2}, D_{3}, \dots, D_{N - 1}$ ，并且同时记录对应的链表节点的指针）。

取出堆顶，把权值累加到答案中。设堆顶对应链表节点的指针为 $p$ ，数值为 $L(p)$ 。在链表中删除 $p$ ， $p->\text{prev}$ 和 $p->\text{next}$ ，在同样的位置插入一个新节点 $q$ ，记录数值 $L(q) = L(p->\text{prev}) + L(p->\text{next}) - L(p)$ 。在堆中也同时删除对应 $p->\text{prev}$ 和 $p->\text{next}$ 的节点，插入对应链表节点 $q$ ，权值为 $L(q)$ 的新节点。

重复上述操作 $K$ 次，就得到了最终的答案。

Huffman树

考虑这样一个问题：给出一棵包含 $n$ 个叶子节点的 $k$ 叉树，其中第 $i$ 个叶子节点带有权值 $w_{i}$ ，要求最小化 $\sum w_{i} * l_{i}$ ，其中 $l_{i}$ 表示第 $i$ 个叶子节点到根节点的距离。该问题的解被称为 $k$ 又Huffman树（哈夫曼树）。

为了最小化 $\sum w_{i} * l_{i}$ ，应该让权值大的叶子节点的深度尽量小。当 $k = 2$ 时，我们很容易想到用下面这个贪心算法来求出二叉Huffman树。

1. 建立一个小根堆，插入这 $n$ 个叶子节点的权值。

2. 从堆中取出最小的两个权值 $w_{1}$ 和 $w_{2}$ ，令 $qns_{1} + = w_{1} + w_{2}$ 。

3. 建立一个权值为 $w_{1} + w_{2}$ 的树节点 $p$ ，令 $p$ 成为权值为 $w_{1}$ 和 $w_{2}$ 的树节点的父亲。

4. 在堆中插入权值 $w_{1} + w_{2}$ 。

5. 重复第 $2 \sim 4$ 步，直至堆的大小为1。

最后，由所有新建的 $p$ 与原来的叶子节点构成的树就是Huffman树，变量ans就是 $\sum w_{i} * l_{i}$ 的最小值。

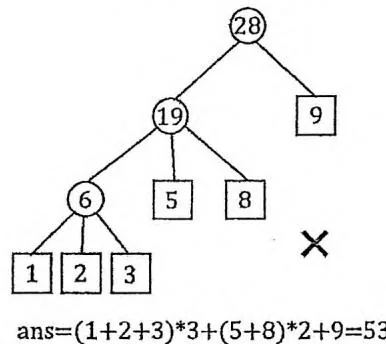
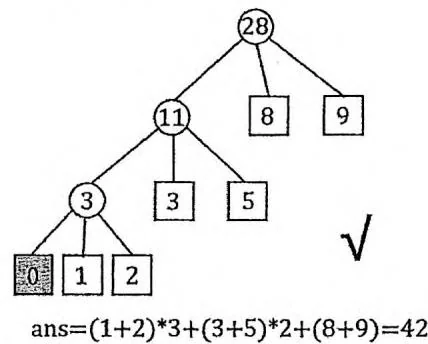
对于 $k(k > 2)$ 又Huffman树的求解，直观的想法是在上述贪心算法的基础上，改为每次从堆中取出最小的 $k$ 个权值。然而，仔细思考可以发现，如果在执行最后一轮循环时，堆的大小在 $2\sim k - 1$ 之间（不足以取出 $k$ 个），那么整个Huffman树的根的子节点个数就小于 $k$ 。这显然不是最优解——我们任意取Huffman树中一个深度最

大的节点，把它改为树根的子节点，就会使 $\sum w_{i} * l_{i}$ 变小。

因此，我们应该在执行上述贪心算法之前，补加一些额外的权值为0的叶子节点，使叶子节点的个数 $n$ 满足 $(n - 1) \mod (k - 1) = 0$ 。也就是说，我们让子节点不足 $k$ 个的情况发生在最底层，而不是根节点处。在 $(n - 1) \mod (k - 1) = 0$ 时，执行“每次从堆中取出最小的 $k$ 个权值”的贪心算法就是正确的。

【例题】合并果子NOIP2004/CODEVS1063

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把任意两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 $n - 1$ 次合并之后，就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为1，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

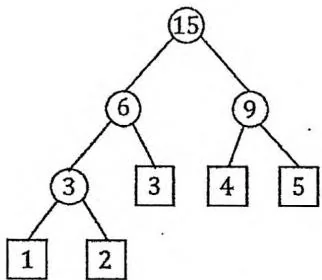
例如有3种果子，数目依次为1，2，9。可以先将1，2堆合并，新堆数目为3，耗费体力为3。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为12，耗费体力为12。所以多多总共耗费体力 $= 3 + 12 = 15$ 。可以证明15为最小的体力耗费值。

因为每次合并消耗的体力等于两堆果子的重量之和，所以最终消耗的体力总和就是每堆果子的重量乘它参与合并的次数。这恰好对应一个二叉Huffman树问题，果子堆的重量就是叶子节点的权值，参与合并的次数就是叶子到根的距离。

建立一个小根堆，插入所有果子堆的重量。不断取出堆中最小的两个值，把它们的和插入堆，同时累加到答案中。直至最后堆的大小为1时，输出答案即可。

【例题】荷马史诗NOI2015/BZOJ4198

追逐影子的人，自己就是影子。——荷马

Allison 最近迷上了文学。她喜欢在一个慵懒的午后，细细地品上一杯卡布奇诺，静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了，Allison 想通过一种编码方式使得它变得短一些。

一部《荷马史诗》中有 $n$ 种不同的单词，从1到 $n$ 进行编号。其中第 $i$ 种单词出现的总次数为 $w_{i}$ 。Allison想要用 $k$ 进制串 $s_{i}$ 来替换第 $i$ 种单词，使得其满足如下要求：

对于任意的 $1 \leq i, j \leq n$ , $i \neq j$ , 都有: $s_i$ 不是 $s_j$ 的前缀。

现在 Allison 想要知道，如何选择 $s_i$ ，才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下，Allison 还想知道最长的 $s_i$ 的最短长度是多少。

一个字符串被称为 $k$ 进制字符串，当且仅当它的每个字符是 0 到 $k - 1$ 之间（包括 0 和 $k - 1$ ）的整数。字符串 Str1 被称为字符串 Str2 的前缀，当且仅当：存在 $1 \leq t \leq m$ ，使得 $Str1 = Str2[1..t]$ 。其中， $m$ 是字符串 Str2 的长度，Str2[1..t] 表示 Str2 的前 $t$ 个字符组成的字符串。

本题所构造的编码方式其实就是Huffman编码。我们把单词的出现次数 $w_{1} \sim w_{n}$ 作为Huffman树叶子节点的权值，然后求出 $k$ 又Huffman树。对于Huffman树每个节点的 $k$ 个分支，分别在边上标记字符 $0 \sim k - 1$ 。

此时，如果把这棵Huffman树看作一棵Trie树，就得到了使总长度最小的编码方式——单词 $i$ 的编码就是从根节点到叶子节点 $i$ 的路径上各条边的字符相连。一个单词不是另一个的前缀，其实就对应着：在Trie树中，所有单词编码的末尾都在叶子节点上，而不在Trie树的一个内部节点上。我们恰好满足了这个性质。

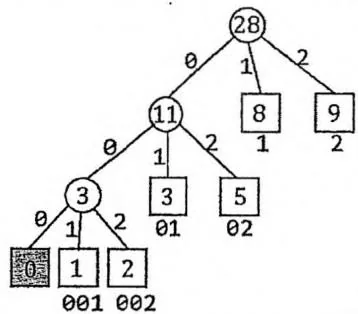
本题还要求最长的 $s_i$ 长度最短，我们只需要在求Huffman树时，对于权值相同的节点，优先考虑当前深度最小（已合并次数最少）的进行合并即可。