特征子空间的几何意义 由等式 A a = λ a \boldsymbol{A} \boldsymbol{a}=\lambda \boldsymbol{a} A a = λ a a \boldsymbol{a} a k a k \boldsymbol{a} k a k a k \boldsymbol{a} k a λ \lambda λ 特征子空间 。
当我们把所有 对应于 λ \lambda λ 零向量 放在一起时,它就构成了一个子空间:
包含零向量 :A 0 = λ 0 A\mathbf{0} = \lambda \mathbf{0} A 0 = λ 0
对加法封闭 :如果 v 1 \mathbf{v}_1 v 1 v 2 \mathbf{v}_2 v 2 V λ V_{\lambda} V λ v 1 + v 2 \mathbf{v}_1 + \mathbf{v}_2 v 1 + v 2 V λ V_{\lambda} V λ
对数乘封闭 :如果 v \mathbf{v} v V λ V_{\lambda} V λ k k k A ( k v ) = k ( A v ) = k ( λ v ) = λ ( k v ) A(k\mathbf{v}) = k(A\mathbf{v}) = k(\lambda \mathbf{v}) = \lambda (k\mathbf{v}) A ( k v ) = k ( A v ) = k ( λ v ) = λ ( k v ) k v k\mathbf{v} k v V λ V_{\lambda} V λ
因此,特征子空间确实是一个向量子空间 。
特征子空间不一定都是直线。如果一个特征值可以对应或求得两个线性无关的特征向量如 a 1 、 a 2 \boldsymbol{a}_1 、 \boldsymbol{a}_2 a 1 、 a 2 a 1 、 a 2 \boldsymbol{a}_1 、 \boldsymbol{a}_2 a 1 、 a 2 A a = λ a \boldsymbol{A} \boldsymbol{a}=\lambda \boldsymbol{a} A a = λ a k 1 a 1 + k 2 a 2 k_1 \boldsymbol{a}_1+k_2 \boldsymbol{a}_2 k 1 a 1 + k 2 a 2
类似地,如果一个特征值对应 S S S S S S
例求矩阵
A = [ 4 6 0 − 3 − 5 0 − 3 − 6 1 ] \boldsymbol{A}=\left[\begin{array}{ccc}
4 & 6 & 0 \\
-3 & -5 & 0 \\
-3 & -6 & 1
\end{array}\right] A = 4 − 3 − 3 6 − 5 − 6 0 0 1 的特征值及特征向量, 并说明其几何意义。
解 由矩阵 A \boldsymbol{A} A
∣ A − λ E ∣ = [ 4 − λ 6 0 − 3 − 5 − λ 0 − 3 − 6 1 − λ ] = ( λ + 2 ) ( λ − 1 ) 2 = 0 |A-\lambda E|=\left[\begin{array}{ccc}
4-\lambda & 6 & 0 \\
-3 & -5-\lambda & 0 \\
-3 & -6 & 1-\lambda
\end{array}\right]=(\lambda+2)(\lambda-1)^2=0 ∣ A − λ E ∣ = 4 − λ − 3 − 3 6 − 5 − λ − 6 0 0 1 − λ = ( λ + 2 ) ( λ − 1 ) 2 = 0 得到特征值 λ 1 = − 2 , λ 2 = λ 3 = 1 \lambda_1=-2, \lambda_2=\lambda_3=1 λ 1 = − 2 , λ 2 = λ 3 = 1 基础解系求法见此处
①把 λ 1 = − 2 \lambda_1=-2 λ 1 = − 2 ( A − λ E ) x = 0 (\boldsymbol{A}-\lambda \boldsymbol{E}) \boldsymbol{x}=\mathbf{0} ( A − λ E ) x = 0
{ 6 x 1 + 6 x 2 = 0 3 x 1 + 3 x 2 = 0 3 x 1 + 6 x 2 − 3 x 3 = 0 \left\{\begin{array}{l}
6 x_1+6 x_2=0 \\
3 x_1+3 x_2=0 \\
3 x_1+6 x_2-3 x_3=0
\end{array}\right. ⎩ ⎨ ⎧ 6 x 1 + 6 x 2 = 0 3 x 1 + 3 x 2 = 0 3 x 1 + 6 x 2 − 3 x 3 = 0 它的基础解系为 ξ = ( − 1 1 1 ) \xi=\left(\begin{array}{c}-1 \\ 1 \\ 1\end{array}\right) ξ = − 1 1 1
所以对应于 λ 1 = − 2 , A \lambda_1=-2, \boldsymbol{A} λ 1 = − 2 , A
x = c ξ = c ( − 1 1 1 ) ( c ≠ 0 , c ∈ R ) x=c \xi=c\left(\begin{array}{c}
-1 \\
1 \\
1
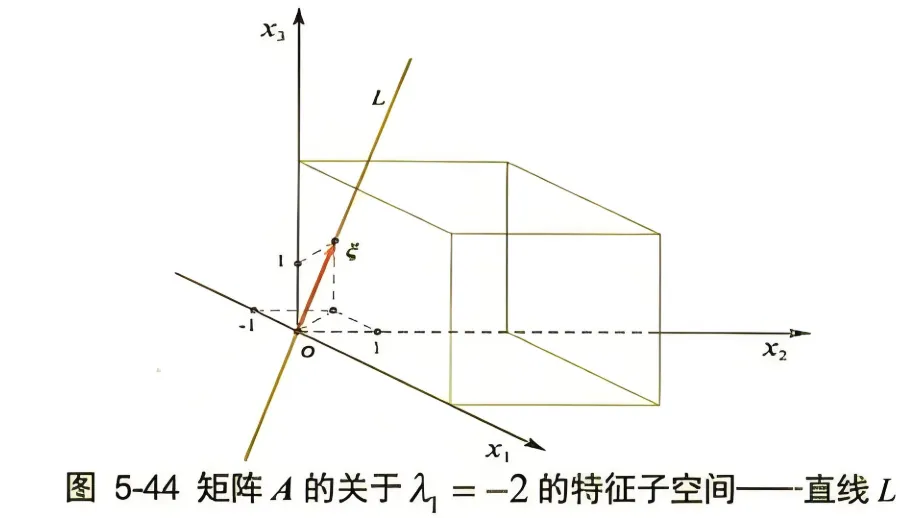
\end{array}\right) \quad(c \neq 0, c \in R ) x = c ξ = c − 1 1 1 ( c = 0 , c ∈ R ) 如图 5-44 所示, 过向量 ξ \xi ξ L L L o o o L L L o o o c ξ c \xi c ξ A \boldsymbol{A} A A \boldsymbol{A} A x \boldsymbol{x} x A \boldsymbol{A} A − 2 x -2 \boldsymbol{x} − 2 x L L L x \boldsymbol{x} x x \boldsymbol{x} x
②把 λ 2 = λ 3 = 1 \lambda_2=\lambda_3=1 λ 2 = λ 3 = 1 ( A − λ E ) x = 0 (A-\lambda E) x=0 ( A − λ E ) x = 0
{ 3 x 1 + 6 x 2 = 0 3 x 1 + 6 x 2 = 0 3 x 1 + 6 x 2 = 0 \left\{\begin{array}{l}
3 x_1+6 x_2=0 \\
3 x_1+6 x_2=0 \\
3 x_1+6 x_2=0
\end{array}\right. ⎩ ⎨ ⎧ 3 x 1 + 6 x 2 = 0 3 x 1 + 6 x 2 = 0 3 x 1 + 6 x 2 = 0 它的基础解系为 ξ 1 = ( − 2 1 0 ) , ξ 2 = ( 0 0 1 ) \xi_1=\left(\begin{array}{c}-2 \\ 1 \\ 0\end{array}\right), \xi_2=\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) ξ 1 = − 2 1 0 , ξ 2 = 0 0 1
所以对应于特征值 λ 2 = λ 3 = 1 , A \lambda_2=\lambda_3=1, \boldsymbol{A} λ 2 = λ 3 = 1 , A
x = c 1 ξ 1 + c 2 ξ 2 = c 1 ( − 2 1 0 ) + c 2 ( 0 0 1 ) \boldsymbol{x}=c_1 \xi_1+c_2 \xi_2=c_1\left(\begin{array}{c}
-2 \\
1 \\
0
\end{array}\right)+c_2\left(\begin{array}{l}
0 \\
0 \\
1
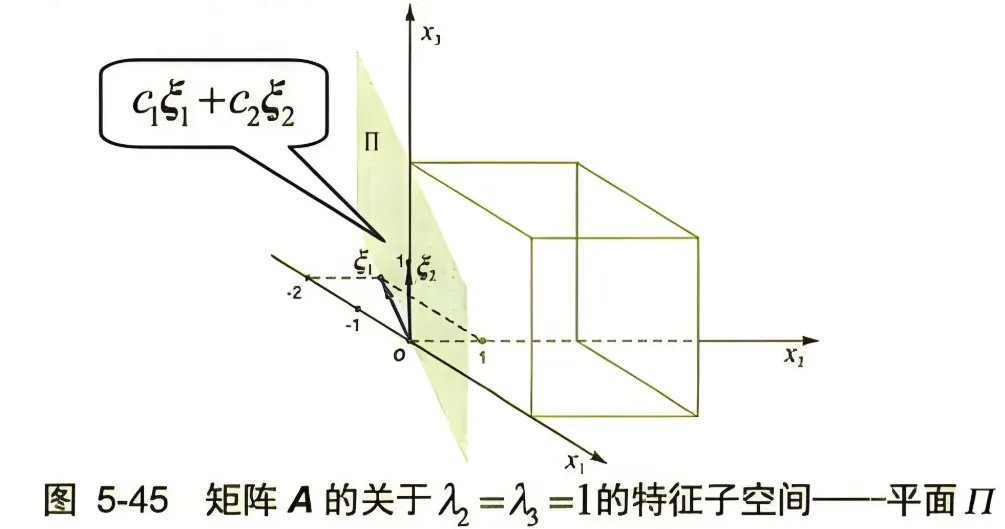
\end{array}\right) x = c 1 ξ 1 + c 2 ξ 2 = c 1 − 2 1 0 + c 2 0 0 1 ( c 1 , c 2 c_1, c_2 c 1 , c 2 Π \Pi Π
如图 5-45 所示, 过向量 ξ 1 , ξ 2 \xi_1, \xi_2 ξ 1 , ξ 2 Π \Pi Π o o o Π \Pi Π o o o c 1 ξ 1 + c 2 ξ 2 c_1 \xi_1+c_2 \xi_2 c 1 ξ 1 + c 2 ξ 2 A \boldsymbol{A} A A \boldsymbol{A} A x \boldsymbol{x} x A \boldsymbol{A} A Π \Pi Π
从上例我们已清楚地看到, A \boldsymbol{A} A A \boldsymbol{A} A
以上举的例子都局限于三维线性空间,同样可推广到 n n n
特征值的代数及几何重数的意义 上面的例子里,在特征多项式方程 ∣ A − λ E ∣ = ( λ + 2 ) ( λ − 1 ) 2 = 0 |\boldsymbol{A}-\lambda \boldsymbol{E}|=(\lambda+2)(\lambda-1)^2=0 ∣ A − λ E ∣ = ( λ + 2 ) ( λ − 1 ) 2 = 0 ( λ + 2 ) (\lambda+2) ( λ + 2 ) ( λ − 1 ) 2 (\lambda-1)^2 ( λ − 1 ) 2
这里有个术语, 一个特征值的求解因式的次数被称之为代数重数 , 特征值的特征子空间的维数被称之为几何重数 。
所以上节矩阵例子里, 特征值-2 的代数重数和几何重数都是 1 ;特征值 1 的代数重数和几何重数都是2。
那我们能否得出代数重数和几何重数是相等的呢?这个结论对一般的矩阵成立吗?答案是不一定成立。
正确的结论是, 特征值的代数重数大于或等于几何重数。
因为有时候代数重数 ⩾ 2 \geqslant 2 ⩾ 2 ⩽ 2 \leqslant 2 ⩽ 2
举个例子。对于三角矩阵:
A = [ a 1 0 b ] \boldsymbol{A}=\left[\begin{array}{ll}
a & 1 \\
0 & b
\end{array}\right] A = [ a 0 1 b ] a a a k ( 1 0 ) k\binom{1}{0} k ( 0 1 ) − x 1 -x_1 − x 1 b b b k ( 1 b − a ) k\binom{1}{b-a} k ( b − a 1 ) a a a b b b
然而, 当 b b b a a a b → a b \rightarrow a b → a b b b a a a k ( 1 b − a ) → k ( 1 0 ) k\binom{1}{b-a} \rightarrow k\binom{1}{0} k ( b − a 1 ) → k ( 0 1 )
当 b b b a a a
一个极端的例子是 n n n
[ a 1 a 1 ⋱ ⋯ a a a ] \left[\begin{array}{lllll}
a & 1 & & & \\
& a & 1 & & \\
& & \ddots & \cdots & \\
& & & a & a \\
& & & & a
\end{array}\right] a 1 a 1 ⋱ ⋯ a a a 这个矩阵只有一个特征值 a a a n n n x 1 x_1 x 1
理解:从坐标空间变换理解代数重根和几何重根 代数重数 :就是特征多项式的根的重数,即
det ( λ I n − A ) = ( λ − λ 1 ) m 1 ( λ − λ 2 ) m 2 ⋯ ( λ − λ s ) m s \operatorname{det}\left(\lambda I _n- A \right)=\left(\lambda-\lambda_1\right)^{m_1}\left(\lambda-\lambda_2\right)^{m_2} \cdots\left(\lambda-\lambda_s\right)^{m_s} det ( λ I n − A ) = ( λ − λ 1 ) m 1 ( λ − λ 2 ) m 2 ⋯ ( λ − λ s ) m s
几何重数 ,是特征矩阵 ( ∣ λ E − A ∣ ) (|\lambda E-A|) ( ∣ λ E − A ∣ )
情况1 :在前面,我们说过,给一个矩阵A A A A A A
情况2 :再有矩阵A A A A A A A A A
A = [ 1 1 1 1 1 1 1 1 1 ] A= \left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1 \\
\end{array}\right] A = 1 1 1 1 1 1 1 1 1 不难发现,这个矩阵就是一个向量,他本身就无法扩张成三维空间,又凭什么认为他能生成新的坐标基呢?
如果我们解A A A
下面这个例子也可以进一步解释:
A = [ 1 3 10 2 4 8 0 0 0 ] A= \left[\begin{array}{lll}
1 & 3 & 10 \\
2 & 4 & 8 \\
0 & 0 & 0 \\
\end{array}\right] A = 1 2 0 3 4 0 10 8 0 不难发现,矩阵A的3个列向量的第三个维度的值都为0,所以,这3个向量都在一个平面如,自然也无法扩张成三维空间。
因此,一个正确的结论是:
如果矩阵A的n n n n n n n n n
下面通过两个例题说明,因为在前面已经介绍了求特征值的方法,因此,这里给出简略解答。
例 判断 A = [ 1 − 1 1 2 − 2 2 − 1 1 − 1 ] A=\left[\begin{array}{ccc}1 & -1 & 1 \\2 & -2 & 2 \\-1 & 1 & -1\end{array}\right] A = 1 2 − 1 − 1 − 2 1 1 2 − 1
解:可以得到他的代数多项式是
λ 2 ( λ + 2 ) = 0 ⇒ { λ 1 = λ 2 = 0 λ 3 = − 2 \lambda^2(\lambda+2)=0 \Rightarrow\left\{\begin{array}{l}
\lambda_1=\lambda_2=0 \\
\lambda_3=-2
\end{array}\right. λ 2 ( λ + 2 ) = 0 ⇒ { λ 1 = λ 2 = 0 λ 3 = − 2 然后可以得到他的3个特征向量,组成一个矩阵为
P = [ 1 − 1 − 1 1 0 − 2 0 1 1 ] P=\left[\begin{array}{ccc}
1 & -1 & -1 \\
1 & 0 & -2 \\
0 & 1 & 1
\end{array}\right] P = 1 1 0 − 1 0 1 − 1 − 2 1 所以,可以对角化,且
P − 1 A P = Λ = [ 0 0 0 − 2 ] P^{-1} A P=\Lambda=\left[\begin{array}{lll}
0 & & \\
& 0 & \\
& 0 & -2
\end{array}\right] P − 1 A P = Λ = 0 0 0 − 2 例 判断A = ∣ 5 − 1 − 1 3 1 − 1 4 − 2 1 ∣ A=\left|\begin{array}{ccc}5 & -1 & -1 \\3 & 1 & -1 \\4 & -2 & 1\end{array}\right| A = 5 3 4 − 1 1 − 2 − 1 − 1 1
解:他的代数多项式
( 3 − λ ) ( 2 − λ ) 2 ⇒ { λ 1 = 3 λ 2 = λ 3 = 2 (3-\lambda)(2-\lambda)^2 \Rightarrow\left\{\begin{array}{l}
\lambda_1=3 \\
\lambda_2=\lambda_3=2
\end{array}\right. ( 3 − λ ) ( 2 − λ ) 2 ⇒ { λ 1 = 3 λ 2 = λ 3 = 2 ① 当λ = 3 \lambda=3 λ = 3
p 1 = ( 1 1 1 ) p_1=\left(\begin{array}{l}
1 \\
1 \\
1
\end{array}\right) p 1 = 1 1 1 ②当λ = 2 \lambda=2 λ = 2
p 2 = ( 1 1 2 ) p_2=\left(\begin{array}{l}
1 \\
1 \\
2
\end{array}\right) p 2 = 1 1 2 可以看到他只有2个特征向量,因此无法对角化。
Q: 如何理解矩阵的不同特征值所对应的特征向量的线性无关性
A:我们知道矩阵的任一特征值 λ \lambda λ V λ = { α ∣ A α = λ α } V_\lambda=\{ \alpha \mid A \alpha =\lambda \alpha \} V λ = { α ∣ A α = λ α }
定理1 设 A A A n n n α 1 , α 2 , ⋯ , α s \alpha _1, \alpha _2, \cdots, \alpha _s α 1 , α 2 , ⋯ , α s λ 1 , λ 2 , ⋯ , λ s \lambda_1, \lambda_2, \cdots, \lambda_s λ 1 , λ 2 , ⋯ , λ s α 1 , α 2 , ⋯ , α s \alpha _1, \alpha _2, \cdots, \alpha _s α 1 , α 2 , ⋯ , α s
较定理 4.6.1 更一般的结论是
定理2 设 A A A n n n λ 1 , λ 2 , ⋯ , λ s \lambda_1, \lambda_2, \cdots, \lambda_s λ 1 , λ 2 , ⋯ , λ s A A A α i 1 , ⋯ , α i r i ( i = 1 , 2 , ⋯ , s ) \alpha _{i 1}, \cdots, \alpha _{i r_i}(i=1,2, \cdots, s) α i 1 , ⋯ , α i r i ( i = 1 , 2 , ⋯ , s ) λ i \lambda_i λ i α 11 , ⋯ , α 1 r 1 \alpha _{11}, \cdots, \alpha _{1 r_1} α 11 , ⋯ , α 1 r 1 α 21 , ⋯ , α 2 r 2 , ⋯ , α s 1 , ⋯ , α s r s \alpha _{21}, \cdots, \alpha _{2 r_2}, \cdots, \alpha _{s 1}, \cdots, \alpha _{s r_s} α 21 , ⋯ , α 2 r 2 , ⋯ , α s 1 , ⋯ , α s r s
上面两定理用特征子空间的语言来描述便是
1 ∘ 1^{\circ} 1 ∘ 2 ∘ 2^{\circ} 2 ∘
 {width=200px}
{width=200px}