在阅读本节前,建议已经掌握了前文介绍的矩阵的秩
对于方程的解与矩阵的秩的关系,初学者可以使用最简单的一次方程帮助记忆。考虑一次方式的三种情况:
① 1x=0 这里系数矩阵A=∣1∣ ,增广矩阵为A′=∣10∣ ,容易知道原方程有唯一的解,所以,如果矩阵的秩等于增广矩阵的秩,方程有解。
② 0x=1 这里矩阵A=∣0∣(因为A=0,所以A没有倒数(即A不可逆)), 增广矩阵为A′=∣10∣ ,容易知道原方程无解,所以,如果矩阵的秩不等于增广矩阵的秩,方程无解。
③ 0x=0 这里矩阵A=∣0∣ ,增广矩阵为A′=∣00∣ ,容易知道原方程有无数解,所以,如果矩阵的秩等于增广矩阵的秩方程有无数的解。
矩阵的秩
先看一下方程组:
⎩⎨⎧x1−2x2−x3+3x42x1−4x2+x3x1−2x2+2x3−3x4=1=5=4 按高斯消元法,首先列出增广矩阵
121−2−4−2−11230−3154 把上面矩阵化为阶梯形矩阵后为
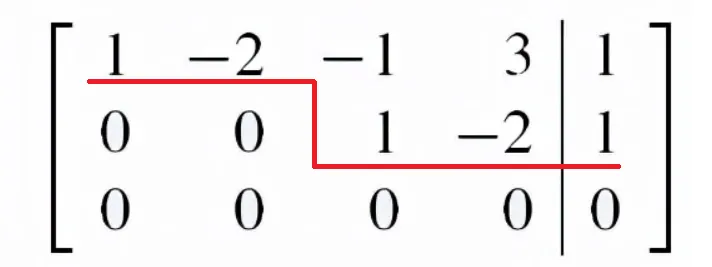 {width=300px}
{width=300px}
如果把上面矩阵系数再还原成方程,则是:
⎩⎨⎧x1−2x2−x3+3x40x1+0x2+x3−2x40x1+0x2+0x3+0x4=1=1=0 仔细观察上面第三个方程,可以发现,不论x取什么值,这个式子都是成立的,换句话说,表面上看这个方程组有3个方程,但是其实真正有效的只有2个方程,第三个方程是“滥竽充数”的。我们把这个“2”就叫做矩阵的秩。再仔细观察一下阶梯形矩阵,他的阶数也正好是2.
结论:矩阵的秩反应的是方程组里有效方程的个数。秩为1表示方程组里有效的方程的个数为1,秩为2表示有效方程个数为2,秩为3表示有效方程个数为3,以此类推
化为最简形矩阵
把上面矩阵化为最简形矩阵,
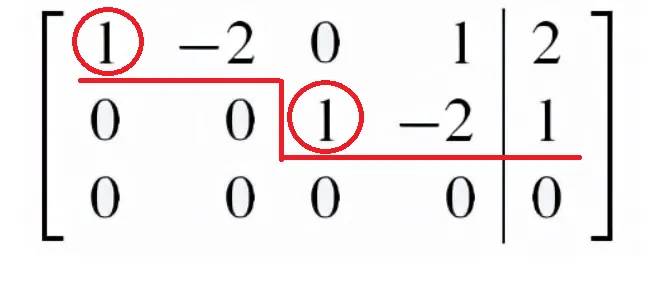 {width=300px}
{width=300px}
然后还原相应的方程组为
⎩⎨⎧x1−2x2+x4x3−2x40=2=1=0 首非零元为 1 在第 1 列和第 3 列,所对应的变量 x1 和 x3 被称为首变量 , x2 和 x4 看成自由变量。更准确地说,在这个例子中,设 x2=C1 和 x4=C2 ,其中 C1 和 C2 是任意的,那么这个方程组就变为
{x1−2C1+C2=2x3−2C2=1 最后方程组的解用参数C1,C2 表示
⎩⎨⎧x1=2+2C1−C2x2=C1x3=1+2C2x4=C2 由于 C1,C2 是任意数,所以这个方程组有无穷解
方程的解和秩的关系
非齐次线性方程组 AX=b
非齐次线性方程组⎩⎨⎧r(A)=r([A:b])=n 时, 方程组有唯一解 r(A)=r([A:b])<n 时, 方程组有无穷多解 r(A)=r([A:b] 时, 方程组无解 记忆方法,以二元为例:
① 这是初中学过的,2个方程2个未知量,所以方程有唯一解。
{x+y=1x−y=0 矩阵的秩r(A)等于增广矩阵的秩r([A:b]等于变量个数n,方程有唯一解。
②x+y=1
矩阵的秩r(A)等于增广矩阵的秩r([A:b],但是小于变量个数n 方程有无穷多个
③ 方程2是方程1的二倍。
{x+y=12x+2y=1 矩阵的秩r(A)不等于增广矩阵的秩r([A:b], 方程无解。
齐次线性方程组 AX=0
齐次线性方程组一定有零解,所以他只有零解和无穷解两个关系。
齐次线性方程组{r(A)=r([A:0])=n 时, 方程组有唯一解 r(A)=r([A:0])<n 时, 方程组有无穷多解 记忆方法,以二元为例:
① 方程有唯一解。
{x+y=0x−y=0 矩阵的秩r(A)等于增广矩阵的秩r([A:b],等于变量个数n 方程有唯一解。
① x+y=0
矩阵的秩r(A)等于增广矩阵的秩r([A:b],但是小于变量个数n 方程有无穷多个
方程组解的判断
例 判断方程组的解
⎩⎨⎧3x+y−4z=x+10z=4x+y+6z=−151 解:对其增广矩阵做变换的
10001010−3405−16−3 如果还原方程组为
⎩⎨⎧x+10zy−34z0=5=−16=−3 这是一个与原方程组等效的方程组,但最后一个意味着 0x+0y+0z=−3 ,所以无解。
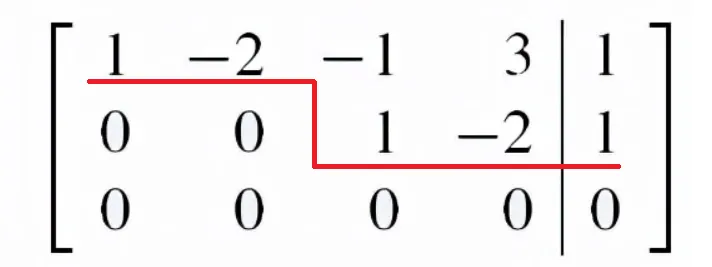 {width=300px}
{width=300px}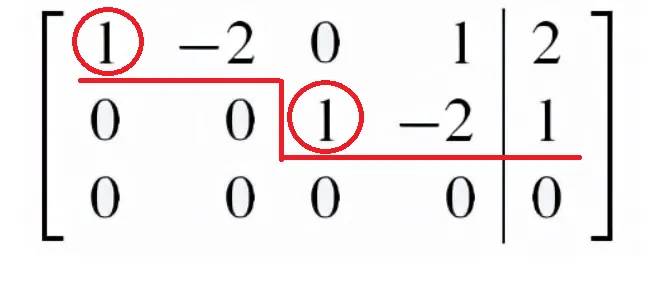 {width=300px}
{width=300px}