2._引论_线性代数的意义 - 线性代数

代数的意义

线性代数（Linear Algebra），包含了线性和代数两层意思。

“代数” 的英文是 Algebra, 源于阿拉伯语, 其本意是“结合在一起”。就是说代数的功能是把许多看似不相关的事物 “结合在一起”, 也就是进行抽象。抽象的目的不是故弄玄虚, 而是为了解决问题的方便, 为了提高效率, 把许多看似不相关的问题化归为一类问题。抽象实际上并不神秘和高深, 我们从小就学会了抽象: 蹒跚学步的时候, 爸妈是这样通过举例子教会孩子数的概念是如何抽象出来的: 这是 1 个苹果, 那是 1 个糖块, 还有 1 个皮球……慢慢地我们忽略了物质上的差别, 明白了 “ 1 ” 这个数量的含义, 并及时地应用上了: “妈妈我要 1 个冰激淋!” 幼儿园及小学时老师也是这样教会我们数的加法运算法则是如何抽象出来的: 2 个苹果加上 3 个苹果是 5 个苹果; 2 个糖块加上 3 个糖块是 5 个糖块; ...... 2 加上 3 就等于 5 , 用符号表示就是 $2+3=5$ 。这样我们进一步地忽略了相加物体的大小、长短及原料的差别, 只关心数量叠加的运算法则。初中的时候, 老师又进一步地教会了我们数及运算法则的进一步抽象:

\begin{aligned} & (1+2)^2=1^2+2(1 \times 2)+2^2 ; \\ & (3+4)^2=3^2+2(3 \times 4)+4^2 ; \end{aligned}

...... 用字母代替数值, 得到完全平方公式: $(a+b)^2=a^2+2 a b+b^2$ 。好了, 抽象又进了一步: 不关心具体数值的运算, 只关心它们的运算规律。到了这时候,我们开始学习一门叫代数的数学课, 代数代数就是用字母代替数进行运算。从某种意义上来说, 代数就是把算术推广到比具体的数更抽象的对象 (运算规则) 上面去。

题外话，“数学”这个名字并不是一开始就有的，在早期的教程，小学的数学被叫做“算术”，初中数学称作“代数”，后来才统一叫做数学。

抽象还可以进一步: 高中时开始知道, 公式 $(a+b)^2=a^2+2 a b+b^2$ 中的字母不仅可以代表数, 还可以同时代表方向一一也就是可以代表向量; 并将其中的乘积 $a^2 、 a b$ 解释为向量内积, 公式仍然成立。画出有向线段来表示公式中的向量 (见图 1-1): $\overrightarrow{O A}=\boldsymbol{a}, \overrightarrow{A B}=\boldsymbol{b}$ , 则 $\overrightarrow{O B}=\boldsymbol{c}=\boldsymbol{a}+\boldsymbol{b}$ 。

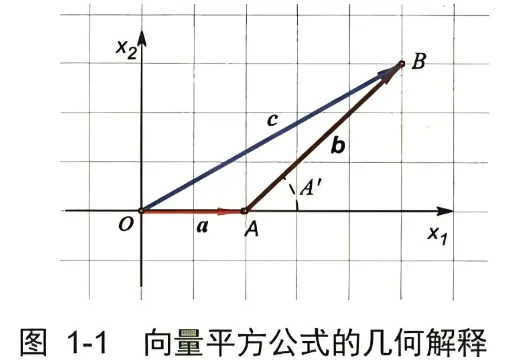$图片$ {width=300px}

所以, 向量的完全平方公式 $(\boldsymbol{a}+\boldsymbol{b})^2=\boldsymbol{a}^2+2 \boldsymbol{a} \cdot \boldsymbol{b}+\boldsymbol{b}^2$ 的几何解释就是

|O B|^2=|O A|^2+|A B|^2+2|O A||A B| \cos A^{\prime}

这就是余弦定理, 当 $A'$ 是直角时就是勾股定理(所以，勾股定理可以看成余弦定理的特殊情况)。将数与向量混为一谈, 立刻从简单的完全平方公式得到勾股定理和余弦定理, 数学的抽象威力由此可见一斑啊!

另外, 抽象还可以沿着另一个途径进行下去。恒等式 $(a+b)^2=a^2+2 a b+b^2$ 中的字母是可变的数, 因此是变量。固定一些变量为常量, 多项式和方程式便出现了。其中一元方程式就有线性方程、二次方程、三次方程......

a x+b=0, a x^2+b x+c=0, a x^3+b x^2+c x+d=0, \cdots

有了各种方程, 如何求解啊? 于是在数学天才们的努力下, 这些方程的根的表示渐渐地知道了: $a x+b=0$ 的根是 $x=-\frac{b}{a}$ ; $a x^2+b x+c=0$ 的根是 $x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a} ;$ 呵, 这些解好完美, 数学真是无懈可击啊。那 $x^2+1=0$ 的根是什么?呃…… $n$ 百年后, 这个问题最终抽象出来虚数的概念 (呵, 把数都抽虚了)。数学在持续完美中: 三元方程式的根被解出来了。四元方程式的根也被解出来了。那五元方程式的根如何表示啊? 如何像二次方程的根一样可以用系数表示出来的形式?这个问题厉害, 解决这个问题伽罗瓦更犀利, 他竟然把运算规律也进行了更抽象的分类, 一下子竟抽出了群的伟大概念!

线性的意义

在说线性，线性其实顾名思义是均匀的意思。比如你匀速跑步，如果你 1 秒跑 2 米，那么 3 秒就跑 6 米，你跑多远是是跟着时间均匀变化的。那么写成公式就是 $s =2 t$ 。

反过来看，时间 $t =1 / 2 s$ ，两者一起均匀变化。那么我们形容跑多远 $s$ 和时间 $t$ 的关系就叫线性相关 ，其实就是均匀相关的意思。

把 $s=2t$ 推广一下， $v=2 w$ , $v$ 和 $w$ 都是向量， $v$ 的箭头长度是 $w$ 的两倍，他们也是互相线性相关。当然，所谓关系一般是形容两个变量的。假如 $w$ 变长 3 倍， $v$ 也跟着变长 3 倍，显然 $3 v=2^*(3 w)$ ，这跟 $s=2 t$ 一样直观。

从另一个角度看， $w$ 变长 $3$ 倍实际上变化量是 $2 w$ ，即 $3 w=w+2 w$ 。那么 $v$ 的变化量 $2v$ 就是 $2 * 2 w$ 。这是显然的。这个角度的好处就是可以用来描述三个向量间的线性相关，比如 $v=2 w+3 u$ 。假设 $w$ 变成 $w+a, u$ 变成 $u+b$ ，那么 $v$ 会变成 $v$ 什么呢？呢，很简单， $v$ 的变化量将直接分为两部分， $w$ 带来的和 $u$ 带来的，因为是线性相关，所以闭着眼睛都知道 $v=2 a+3 b$ 。代入回去检验一下， $v+(2 a+3 b)=2( w + a )+3( u + b ) 。$

如果记得微积分就会记得，二元函数的全微分就是分别算 dx 方向和 dy 方向的最后加起来，同样， $v=2 w+3 u$ 实际上也是一回事， $v$ 的变化由 $w$ 和 $u$ 各自变化带来的。当然，如果不把 $v$ 看做 $w$ 和 $u$ 的因变量，让三个向量都平等也是可以的。我们看 $v=2 w+3 u$ ，所以 $w=1 / 2 v-3 / 2 u$ ， $u=1 / 3 v-2 / 3 w$ ， $v 、 w 、 u$ 三个都是一起线性变化的，不用分谁是因变量，谁是自变量。所以大学里线性代数有个重要概念，向量组的线性相关和线性无关，所谓的线性相关就是无论有多少个向量，彼此这样线性互相关联。

线性结构

现在就能讲线性空间了。上面提到 $v=2 w+3 u$ ，那必然还可以有像 $a=w-5 u, b=7 w+2 u$ 之类的无数个跟 $w$ 和 $u$ 存在线性相关的向量，那么这些所有的向量的集合就组成了以 $w$ 和 $u$ 为基的向量空间，假如这个空间的名字是 $V$ 。那么 $V$ 里面随便抓一个向量比如 $c$ 出来， $c 、 w 、 u$ 三个家伙都是线性相关的，简单说 $V$ 里面的家伙，互相之间都算亲戚，比如上面的例子， $v$ 就可以写成坐标 $(2,3), a=(1,-5), ~ b=(7,2)$ ，这个空间里面互相之间的亲戚关系就是这个空间的结构，也就是线性相关结构，简称线性结构。

矩阵的作用

那么线性代数里的矩阵是啥呢？矩阵就是传递线性空间内部结构的映射，线性空间的结构就是线性结构，所以叫线性映射。比如我现在有个线性空间 $V$ ，二维的，还有一个线性空间 $W$ ，三维的。然后我现在有个矩阵 $A$ 。对 $V$ 中一个向量 $v$ ，那么映射后 $Av$ 就是 $W$ 里的元素了。那么如果 $V$ 中原来三个向量 $v 、 w 、 u$ 的亲戚关系是 $v=2 w+3 u$ 。那么他们跑到 $W$ 里变成 $A v 、 A w 、 A u$ 后，必须也是继续保持 $A v=2 A w+3 A u$ 这种亲戚关系，即线性结构不变。那么矩阵 $A$ 就显然得有 $A v=2 A w+3 A u=A 2 w+A 3 u=A(2 w+3 u)$ 这种类似乘法分配律的运算时变形能力。

一句话介绍完矩阵并理解他是不现实的，矩阵的强大作用只有在后面学习中，才能慢慢体会得到。

线性映射和线性变换

线性映射和线性变换这两个概念类似，如果是在同一个维度通常称作变换，如果再不同维度通常称作映射。

比如，你把一个二维的圆转换为二维的椭圆，转换前后都在二维里，我们称为变换，如果你把灯光照射三维空间的球，在墙面上形成一个圆，这是从三维球体转换为了二维圆，一般称呼为映射。

线性空间

上面的“均匀性”更本质就是可加性和比例性，把上面这些功能合起来进行抽象，然后给他一个名字：线性空间。线性代数中的核心抽象概念是线性空间, 即所谓的要满足 "加法" 和 "数乘" 等八条公理的元素的集合。也就是说, 只要某个集合里的元素满足那么几条公理, 元素之间的变化满足这些规律, 我们就可以对这个集合进行一系列线性化处理和分析, 这个集合就叫线性空间。这个陌生的集合的性质和结构特点我们一下子就全知道了, 因为宇宙间的所有的线性空间类的集合的性质都一样, 地球人都知道 (如果地球人都学了线性代数的话)。多么深刻而美妙的结论！这就是代数的一个抽象特性。

线性空间的八大基本性质（设线性空间为 $V$ ，元素 $\alpha, \beta, \gamma \in V$ ，数 $k, l \in \mathbb{F}$ ， $\mathbb{F}$ 为数域，通常是实数域 $\mathbb{R}$ 或复数域 $\mathbb{C}$ ）

线性空间八大基本性质表

序号	性质名称	数学表达式	核心含义解读
1	加法交换律	$\alpha + \beta = \beta + \alpha$	两个元素相加时，交换元素顺序，最终结果保持不变
2	加法结合律	$(\alpha + \beta) + \gamma = \alpha + (\beta + \gamma)$	三个元素相加时，改变加法运算的先后顺序（即改变括号位置），最终结果保持不变
3	加法零元存在性	存在唯一 $0\in V$ ，对任意 $\alpha\in V$ ，有 $\alpha + 0 = \alpha$	线性空间中存在“零向量”，其与任意元素相加后，仍等于该元素本身
4	加法负元存在性	对任意 $\alpha\in V$ ，存在唯一 $\beta\in V$ （记 $\beta=-\alpha$ ），有 $\alpha + \beta = 0$	线性空间中任意元素都有对应的“负向量”，该元素与其负向量相加，结果为零向量
5	数乘单位元存在性	存在 $1\in\mathbb{F}$ ，对任意 $\alpha\in V$ ，有 $1\cdot\alpha = \alpha$	用数域中的单位元“1”对数乘线性空间中的任意元素，结果仍等于该元素本身
6	数乘结合律	$k\cdot(l\cdot\alpha) = (k\cdot l)\cdot\alpha$	先将两个数相乘，再用乘积数乘元素；与先对数乘一个数，再用另一个数乘结果，两者等价
7	数乘对加法的分配律（对数域加法）	$(k + l)\cdot\alpha = k\cdot\alpha + l\cdot\alpha$	两个数相加后数乘某一元素，等于这两个数分别数乘该元素后，再将结果相加
8	数乘对加法的分配律（对空间加法）	$k\cdot(\alpha + \beta) = k\cdot\alpha + k\cdot\beta$	用某一个数乘两个元素的和，等于用这个数分别乘两个元素后，再将结果相加

注：上表由AI自动生成，请酌情参考。

上面虽然是八大性质，但是核心其实就2个：可加性和可比性。

线性问题为什么重要？

"线性" 是数学中使用十分广泛的词汇。我们常说的 "一次方程" 和 "一次函数"，原本都是 "线性方程（Linear Equation）" 和 "线性函数（Linear Function）"。在大学里，流行 "线性"、"线性代数"、"线性变换"、"线性常微分方程"、"线性偏微分方程"、 "线性规划"、"线性算子"、"线性泛函"、"线性控制系统"、"拟线性"、"准线性"等。为什么以向量为基本对象的 "线性数学" 会流行呢?

从科技实践中来的数学问题无非分为两类：一类线性问题，一类非线性问题。线性问题是研究最久、理论最完善的；而非线性问题则可以在一定基础上转化为线性问题求解。因此遇到一个具体的问题，首先判断是线性还是非线性的；其次若是线性问题如何处理，若是非线性问题如何转化为线性问题。

对于非线性问题通常转换为线性问题进行处理。例如 $y=e^x$ 这是一个指数函数，取对数后变为 $lny=x$ ，如果令 $\hat{y}=lny,\hat{x}=x$ ,则原本指数函数就会变成线性函数 $\hat{y}=\hat{x}$ ,在高中阶段学习的一元线性回归应用例题2 就演示了此方法

在比如《高等数学》里的多元微分，就是使用线性近似替代非线性。详见全微分

相对于 "非线性数学" 来说, 线性数学比较简单。微积分学的基本思想是 "以直代曲",局部地以切线代替曲线。于是，在某种条件下，微分方程就可以近似地变成 "线性代数方程组"。20世纪有了电子计算机, 无论未知数的个数 $n$ 有多大, 都可以设法计算。于是, 把以 $n$ 维向量为对象的线性方程组搞清了, 许多复杂的数学问题也就有解了 (至少是近似的)。

既然线性问题如此重要, 到底什么是线性呢? 下面我们通过介绍一个例子来逐渐地把握 "线性" 这个数学的核心概念。

比如平面 $z=a x+b y$ ，我们往 $x$ 方向走一个单位， $z$ 就会增加 $a$ ，往 $y$ 走一个单位， $z$ 就会增加 $b$ ，你同时随便往 $x$ 走 $0.5$ 个单位，往 $y$ 走 $0.6$ 个单位， $z$ 对应增加 $0.5 a+0.6 y$ ，这就是线性的力量！这个函数 $z=a x+b y$ 你可以把他看成函数，也可以把他看成向量，本质都一样的，所以，有时候我们会说：

线性函数就是线性向量，线性向量也是线性函数

到底是函数还是向量，只是你人为的理解，而数学看的是本质。