34._矩阵的特征值分解QAQ_T

S=QΛQT S=Q \Lambda Q^{\mathrm{T}} 特征值分解图解

注意：本文需要特征值与特征向量知识，相加 特征值与特征向量

所有对称矩阵 SS 都必须有实特征值和正交特征向量．特征值是 Λ\Lambda 的对角元素，特征向量在 QQ 中．

图片

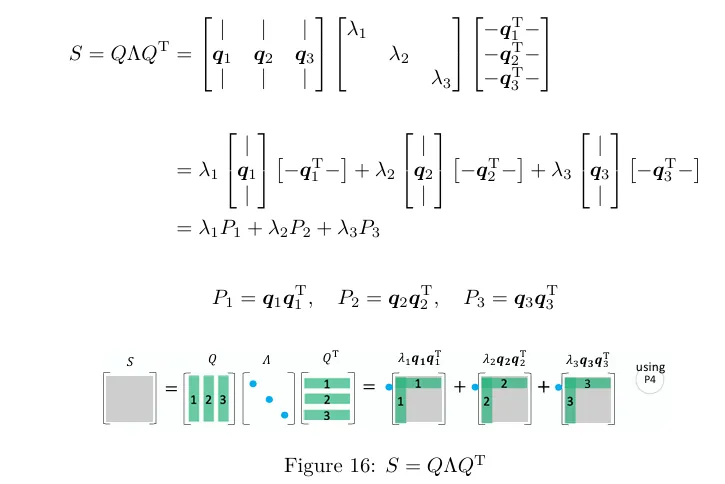
一个对称矩阵 SS 通过一个正交矩阵 QQ 和它的转置矩阵，对角化为 Λ\Lambda 。然后被分解为一阶投影矩阵 P=qqTP=q q^{\mathrm{T}}的组合．这就是谱定理．

S=ST=λ1P1+λ2P2+λ3P3QQT=P1+P2+P3=IP1P2=P2P3=P3P1=OP12=P1=P1T,P22=P2=P2T,P32=P3=P3T\begin{gathered} S=S^{\mathrm{T}}=\lambda_1 P_1+\lambda_2 P_2+\lambda_3 P_3 \\ Q Q^{\mathrm{T}}=P_1+P_2+P_3=I \\ P_1 P_2=P_2 P_3=P_3 P_1=O \\ P_1^2=P_1=P_1^{\mathrm{T}}, \quad P_2^2=P_2=P_2^{\mathrm{T}}, \quad P_3^2=P_3=P_3^{\mathrm{T}} \end{gathered}

线性代数中一个非常核心且强大的概念——矩阵的特征值分解（Eigen Decomposition），也称为谱分解（Spectral Decomposition）。

1. 核心思想与定义

特征值分解的目标是将一个方阵 AA 分解为一组特征向量和特征值，从而揭示其内在的几何性质和结构。

定义： 对于一个 n×nn \times n 的方阵 AA，如果它存在 nn 个线性无关的特征向量，那么它可以被分解为以下形式：

A=PΛP−1A = P \Lambda P^{-1}

其中：

  • PP 是一个可逆矩阵，其列向量是 AA 的 nn 个线性无关的特征向量（p1,p2,...,pn\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_n）。

  • Λ\Lambda (Lambda) 是一个对角矩阵，其主对角线上的元素是 AA 的特征值（λ1,λ2,...,λn\lambda_1, \lambda_2, ..., \lambda_n），这些特征值的排列顺序与 PP 中特征向量的排列顺序一一对应。

分解后的形式如下：

A=[∣∣∣p1p2⋯pn∣∣∣][λ10⋯00λ2⋯0⋮⋮⋱⋮00⋯λn][∣∣∣p1p2⋯pn∣∣∣]−1A = \begin{bmatrix} | & | & & | \\ \mathbf{p}_1 & \mathbf{p}_2 & \cdots & \mathbf{p}_n \\ | & | & & | \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix} \begin{bmatrix} | & | & & | \\ \mathbf{p}_1 & \mathbf{p}_2 & \cdots & \mathbf{p}_n \\ | & | & & | \end{bmatrix}^{-1}

2. 直观理解：矩阵的“自然坐标系”

你可以将特征值分解理解为：在由特征向量构成的“自然坐标系”下，矩阵 AA 所代表的线性变换被简化为纯粹的缩放（Stretching/Scaling）操作。

  • 特征向量（PP 的列） 定义了变换的“主方向”。在这些方向上，变换的效果最简单。

  • 特征值（Λ\Lambda 的对角元素） 定义了在这些“主方向”上变换的缩放因子。

  • ∣λ∣>1|\lambda| > 1：拉伸

  • 0<∣λ∣<10 < |\lambda| < 1：压缩

  • λ<0\lambda < 0：反向

操作过程：

  1. P−1xP^{-1} \mathbf{x}：将向量 x\mathbf{x} 从标准坐标系变换到由特征向量构成的“自然坐标系”下。

  2. Λ(P−1x)\Lambda (P^{-1} \mathbf{x})：在新的坐标系下，对向量进行简单的缩放（每个分量乘以对应的特征值）。

  3. P(ΛP−1x)P (\Lambda P^{-1} \mathbf{x})：将缩放后的向量再变换回原始的标准坐标系。

整个过程 Ax=PΛP−1xA \mathbf{x} = P \Lambda P^{-1} \mathbf{x} 等价于在原始坐标系下进行复杂的变换，但在“自然坐标系”下看，却只是一系列简单的缩放。

3. 分解的条件与步骤

前提条件： 一个 n×nn \times n 矩阵 AA 可以进行特征值分解的充要条件是：它拥有 nn 个线性无关的特征向量。

  • 满足这个条件的矩阵被称为可对角化矩阵（Diagonalizable Matrix）。

  • 充分非必要条件：如果 AA 是实对称矩阵（Symmetric Matrix），那么它必然有 nn 个正交的特征向量，并且可以进行特征值分解。

分解步骤：

  1. 求特征值（Find Eigenvalues）： 解特征方程 det⁡(A−λI)=0\det(A - \lambda I) = 0，得到 nn 个特征值 λ1,λ2,...,λn\lambda_1, \lambda_2, ..., \lambda_n。 （II 是单位矩阵）

  2. 求特征向量（Find Eigenvectors）： 对每个特征值 λi\lambda_i，求解齐次线性方程组 (A−λiI)v=0(A - \lambda_i I) \mathbf{v} = \mathbf{0}，得到对应的特征向量 pi\mathbf{p}_i。

  3. 构造矩阵 PP 和 Λ\Lambda：

  • 将求得的 nn 个线性无关的特征向量 p1,p2,...,pn\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_n 作为列向量，组成矩阵 P=[p1,p2,...,pn]P = [\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_n]。

  • 将对应的特征值按相同顺序放在对角线上，组成对角矩阵 Λ=diag(λ1,λ2,...,λn)\Lambda = \text{diag}(\lambda_1, \lambda_2, ..., \lambda_n)。

  1. 验证分解： 检查 A=PΛP−1A = P \Lambda P^{-1} 是否成立。

4. 例子

设矩阵 A=[2112]A = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}，求其特征值分解。

Step 1: 求特征值 解特征方程：

det⁡(A−λI)=det⁡[2−λ112−λ]=(2−λ)2−1=0\det(A - \lambda I) = \det \begin{bmatrix} 2-\lambda & 1 \\ 1 & 2-\lambda \end{bmatrix} = (2-\lambda)^2 - 1 = 0
λ2−4λ+3=0  ⟹  (λ−1)(λ−3)=0\lambda^2 - 4\lambda + 3 = 0 \implies (\lambda - 1)(\lambda - 3) = 0

特征值为：λ1=1\lambda_1 = 1, λ2=3\lambda_2 = 3。

Step 2: 求特征向量

  • 对于 λ1=1\lambda_1 = 1： (A−I)v=[1111][v1v2]=0(A - I)\mathbf{v} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \mathbf{0} 解得：v1+v2=0v_1 + v_2 = 0，取 p1=[1−1]\mathbf{p}_1 = \begin{bmatrix} 1 \\ -1 \end{bmatrix}。

  • 对于 λ2=3\lambda_2 = 3： (A−3I)v=[−111−1][v1v2]=0(A - 3I)\mathbf{v} = \begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \mathbf{0} 解得：−v1+v2=0-v_1 + v_2 = 0，取 p2=[11]\mathbf{p}_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}。

Step 3: 构造 PP 和 Λ\Lambda

P=[p1p2]=[11−11],Λ=[λ100λ2]=[1003]P = \begin{bmatrix} \mathbf{p}_1 & \mathbf{p}_2 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix}, \quad \Lambda = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix}

计算 PP 的逆：

P−1=1det⁡(P)[1−111]T=12[11−11]P^{-1} = \frac{1}{\det(P)} \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}^T = \frac{1}{2} \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix}

Step 4: 验证

PΛP−1=[11−11][1003]12[11−11]=12[13−13][11−11]=12[(1−3)(1+3)(−1−3)(−1+3)]=12[−24−42]=[2112]=AP \Lambda P^{-1} = \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 3 \end{bmatrix} \frac{1}{2} \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} 1 & 3 \\ -1 & 3 \end{bmatrix} \begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} = \frac{1}{2} \begin{bmatrix} (1-3) & (1+3) \\ (-1-3) & (-1+3) \end{bmatrix} = \frac{1}{2} \begin{bmatrix} -2 & 4 \\ -4 & 2 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} = A

验证成功！

5. 特殊情形：实对称矩阵的谱定理

如果 AA 是一个实对称矩阵（A=ATA = A^T），那么它的特征值分解具有更优美的性质：

  1. 所有特征值都是实数。

  2. 不同特征值对应的特征向量相互正交。

  3. 它可以被分解为：

A=QΛQTA = Q \Lambda Q^T

其中 QQ 是一个正交矩阵（由单位化的、相互正交的特征向量组成，满足 Q−1=QTQ^{-1} = Q^T），Λ\Lambda 是对角矩阵。

这种形式避免了求逆运算，计算和应用起来更加方便。主成分分析（PCA） 的核心就是基于实对称矩阵（协方差矩阵）的这个分解。

6. 应用场景

特征值分解是理解和简化复杂线性变换的基石，其应用极其广泛：

  • 解耦系统：在微分方程和动力系统中，可以将耦合的系统解耦为独立的单变量系统。

  • 主成分分析（PCA）：用于数据降维，找到数据中方差最大的方向（即特征向量方向）。

  • 振动分析：在机械工程中，用于求解结构的固有频率（特征值）和振型（特征向量）。

  • 量子力学：可观测量的算符对应的矩阵的特征值代表可能的测量结果。

  • 矩阵函数：计算矩阵的幂 Ak=PΛkP−1A^k = P \Lambda^k P^{-1} 或指数 eA=PeΛP−1e^A = P e^{\Lambda} P^{-1} 变得非常简单。

7. 总结

特性描述
形式A=PΛP−1A = P \Lambda P^{-1} （对称阵： A=QΛQTA = Q \Lambda Q^T)
矩阵P/Q可逆矩阵/正交矩阵，其列向量是 AA 的特征向量。
矩阵Λ对角矩阵，其元素是 AA 的特征值。
核心思想在由特征向量定义的“自然坐标系”下，变换简化为纯粹的缩放。
前提条件AA 必须是可对角化的，即拥有 nn 个线性无关的特征向量。
主要应用解耦系统、PCA降维、振动分析、计算矩阵函数。

简单来说，特征值分解为我们提供了一种“翻译”工具，能将一个复杂的矩阵变换，用最简单的缩放操作来描述。它是连接线性代数理论和应用的桥梁。

上一章33._矩阵的QR分解
下一章35._矩阵的奇异值SVD分解