矩阵右乘是列变换
下面例子演示了右乘的意思,对于A×B=C
123456789200010001=246456789 从结果看,
一个矩阵A右乘一个矩阵B,相当于对矩阵A的列进行了列变换。
记忆口诀:左乘是行变换,右乘是列变换
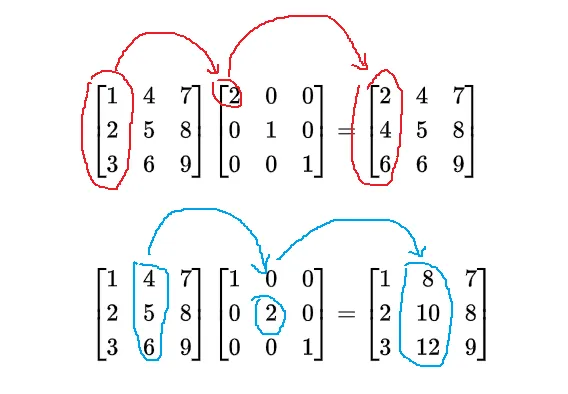
初等矩阵右乘的效果
若 E 是单位矩阵经过一次 列初等变换 得到的初等矩阵,那么 AE 就是对 A 做同样的列变换。
例如:
E=100001010(交换第2、3列)
右乘它:AE 会交换 A 的第 2 列与第 3 列。
E=1000k0001(第 2 列乘 k)
右乘它:AE 会将 A 的第 2 列乘以 k。
E=100c10001(第 1 列加 c 倍第 2 列)
右乘它:AE 会将 A 的第 1 列加上 c 倍第 2 列。
例如
A=147258369×102010001=71625258369. 新第 1 列 = 原第 1 列 + 2 × 原第 3 列
新第 2 列 = 原第 2 列
新第 3 列 = 原第 3 列
使用列变换求逆矩阵
列变换等价于右乘一个初等矩阵E,因为这个关系,给你一个矩阵A,如果A可逆,那么通过初等列变换总能变成单位矩阵E,写成矩阵乘法就是:
AP1P2P2...Pk⋅=E 进一步的,因为A−1⋅A=E, 所以
A−1=P1P2P2...Pk 从上面可以得到逆矩阵的求法,
给你一个矩阵A,把他和单位矩阵E进行按列合并,然后使用列变换,上边化成E,则下边就是A−1
即
[AE]→[EA−1] 注意:在求解方程或者逆矩阵里,我们几乎都不使用列变换,此处稍微了解即可。
从上面可知,加上给你一个矩阵方程XA=B,可以有两种解法:
①解法一:直接使用列变换求解。
②解法二:XA=B 两边去转置的 ATXT=BT 这样又变成左乘的形式了,然后使用行变换,只是解出来的是XT,只要再转置一下即可得X
具体解释清参考 逆矩阵 ,他也是XA=B 方差的标准解法,见 逆矩阵解方程
矩阵右乘向量
对于矩阵右乘向量,通常使用转置进行理解

矩阵转置后又变成了左乘模式,但是此时使用的是转置,
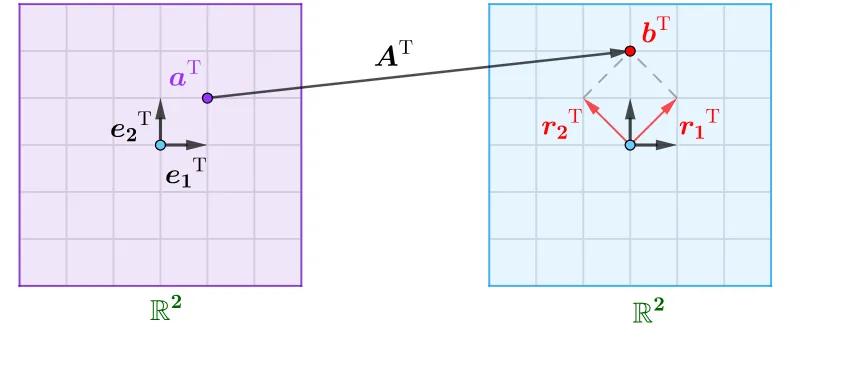 具体可以参考 基变换的几何意义
具体可以参考 基变换的几何意义
矩阵左乘向量图解
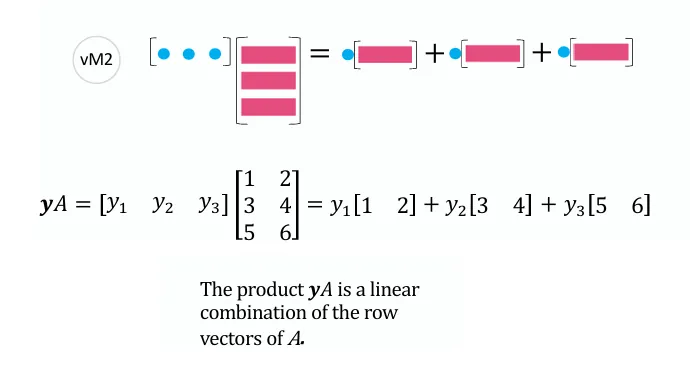
[x1x2x3]a11a21a31a12a22a32a13a23a33=x1[a11a12a13]+x2[a21a22a23]+x3[a31a32a33] 观察上式,用x行向量左乘矩阵 A ,相当于对矩阵 A 中的行向量做线性组合,线性组合的系数就是行向量 x 中的每个对应位置的元素。
矩阵右乘
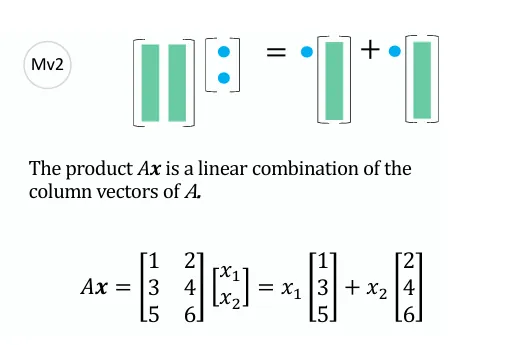
a11a21a31a12a22a32a13a23a33x1x2x3=x1a11a21a31+x2a12a22a32+x3a13a23a33 观察上式,不难发现,矩阵A右乘向量x 中的列向量 相当于对矩阵A的列做线性组合。
由此的下面定理
设 A 是一个 m×n 的矩阵,对 A 进行一次初等行变换相当于在 A 的左边乘一个相应类型的 m 阶初等矩阵;对 A 进行一次初等列变换相当于在 A 的右边乘一个相应类型的 n 阶初等矩阵.
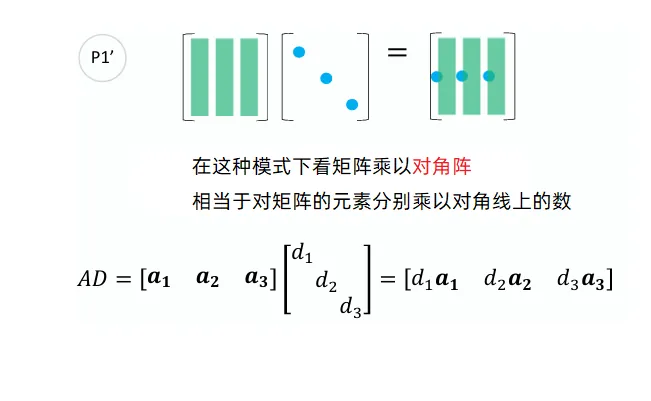
矩阵乘以对角矩阵
右乘对角矩阵
矩阵右乘对角矩阵相当于对列乘积相应的倍数
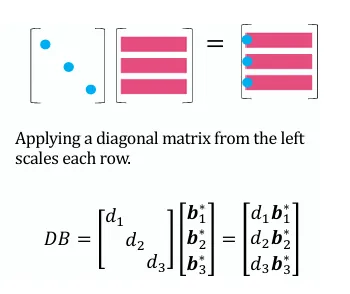
左乘对角矩阵
矩阵左乘对角矩阵相当于对行乘积相应的倍数
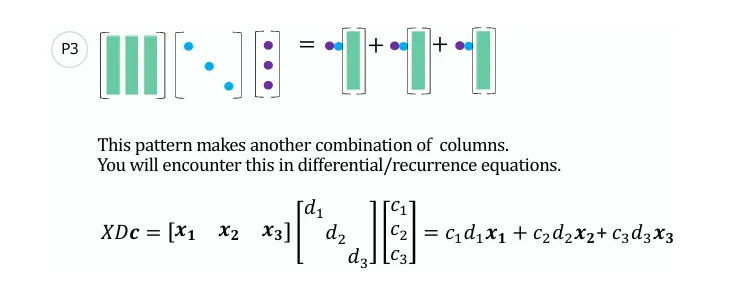
矩阵乘以对角矩阵和列向量
这种也可以看成列的组合。


 具体可以参考 基变换的几何意义
具体可以参考 基变换的几何意义



