阅读本文前,最好理解了 矩阵乘法
在计算机图形学里,大量应用矩阵,这里介绍几个常见的变换。
图形缩放 缩放变换中,如果一个图片以原点 ( 0 , 0 ) (0,0) ( 0 , 0 ) s s s ( x , y ) (x, y) ( x , y )
x ′ = s x y ′ = s y \begin{aligned}
& x^{\prime}=s x \\
& y^{\prime}=s y
\end{aligned} x ′ = s x y ′ = sy 写成矩阵形式为:
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
s_x & 0 \\
0 & s_y
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] 当然,我们也可以给 x 轴和 y 轴不同的缩放倍数 s x s x s x s y s y sy
[ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] . . . ( 图像缩放公式 ) \boxed{
\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
s_x & 0 \\
0 & s_y
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] ...(\text{图像缩放公式})
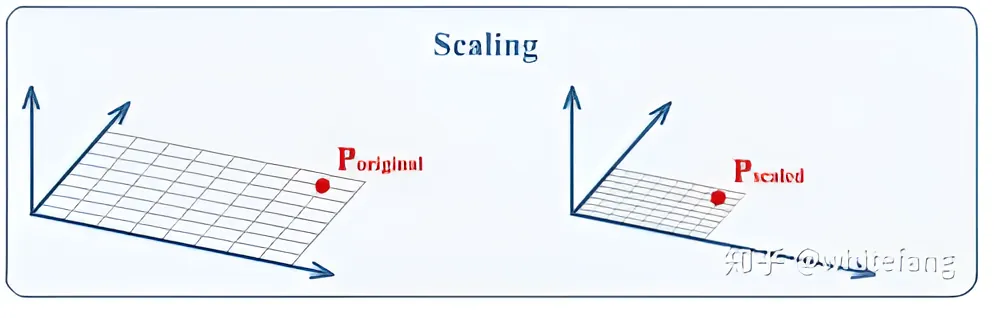
} [ x ′ y ′ ] = [ s x 0 0 s y ] [ x y ] ... ( 图像缩放公式 ) 下图展示了图像缩放示意图
例 下面矩阵乘法显示一个向量[ 1 , 1 ] [1,1] [ 1 , 1 ] [ 2 , 1 ] [2,1] [ 2 , 1 ] 一个向量左乘对角阵相当于对向量各维坐标值进行缩放,缩放的比例就是对角阵元素的值 。当然了,这里的向量缩放这里也可以看成坐标轴进行缩放,两者是等价的
[ 2 0 0 1 ] [ 1 1 ] = [ 2 1 ] \left[\begin{array}{ll}
2 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
1 \\
1
\end{array}\right]=\left[\begin{array}{l}
2 \\
1
\end{array}\right] [ 2 0 0 1 ] [ 1 1 ] = [ 2 1 ] 从几何意义上看,向量从A B ⃗ \vec{AB} A B A C ⃗ \vec{AC} A C
你也可以从物理上理解,一个物体原先速度为( 1 , 1 ) (1,1) ( 1 , 1 )
图像旋转 我们默认旋转变换(Rotate)都绕着原点( 0 , 0 ) (0, 0) ( 0 , 0 ) ( x , y ) (x,y) ( x , y ) ( 0 , 0 ) (0,0) ( 0 , 0 ) θ \theta θ
[ x ′ y ′ ] = [ cos θ − sin θ sin θ cos θ ] [ x y ] . . . ( 图像旋转公式 ) \boxed
{
\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] ...(\text{图像旋转公式})
} [ x ′ y ′ ] = [ cos θ sin θ − sin θ cos θ ] [ x y ] ... ( 图像旋转公式 ) 证明 我们在直角坐标系中绘制一个边长为 1 的正方形,点 A A A ( 1 , 0 ) (1,0) ( 1 , 0 ) B B B ( 0 , 1 ) (0,1) ( 0 , 1 ) ( 0 , 0 ) (0,0) ( 0 , 0 ) θ \theta θ
我们设原坐标里任一点( x , y ) (x,y) ( x , y ) ( x ′ , y ′ ) (x',y') ( x ′ , y ′ )
[ x ′ y ′ ] = [ A B C D ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ A C B D ] [ x y ] 接下来去两个特殊点,代入点 A A A ( 1 , 0 ) (1,0) ( 1 , 0 )
[ cos θ sin θ ] = [ A B C D ] [ 1 0 ] \left[\begin{array}{c}
\cos \theta \\
\sin \theta
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
1 \\
0
\end{array}\right] [ cos θ sin θ ] = [ A C B D ] [ 1 0 ] 解方程得到:
A = cos θ C = sin θ \begin{aligned}
& A=\cos \theta \\
& C=\sin \theta
\end{aligned} A = cos θ C = sin θ 代人点 B B B ( 0 , 1 ) (0,1) ( 0 , 1 )
[ − sin θ cos θ ] = [ A B C D ] [ 0 1 ] \left[\begin{array}{c}
-\sin \theta \\
\cos \theta
\end{array}\right]=\left[\begin{array}{ll}
A & B \\
C & D
\end{array}\right]\left[\begin{array}{l}
0 \\
1
\end{array}\right] [ − sin θ cos θ ] = [ A C B D ] [ 0 1 ] 解方程得到:
B = − sin θ D = cos θ \begin{aligned}
& B=-\sin \theta \\
& D=\cos \theta
\end{aligned} B = − sin θ D = cos θ 因此,坐标旋转公式为
A rotate = [ cos θ − sin θ sin θ cos θ ] A_{\text {rotate }}=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right] A rotate = [ cos θ sin θ − sin θ cos θ ] 下图显示了一个图形旋转
例 考虑θ = 45 ∘ \theta=45^{\circ} θ = 4 5 ∘ cos θ = sin θ = 2 2 \cos \theta=\sin \theta= \frac{\sqrt{2}}{2} cos θ = sin θ = 2 2 A A A
A = [ 2 2 − 2 2 2 2 2 2 ] \boldsymbol{A}=\left[\begin{array}{cc}
\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}
\end{array}\right] A = [ 2 2 2 2 − 2 2 2 2 ] 这意味着任何一个向量乘以该矩阵将旋转45 ∘ 45^{\circ} 4 5 ∘
矩阵的旋转与缩放 在一维里,一个向量乘以− 1 -1 − 1 180 180 180 i i i i i i 90 90 90
一个矩阵乘以一个向量, 一般将会对向量的几何图形进行旋转和伸缩变化。常见的一个例子就是旋转矩阵, 旋转矩阵只对向量进行旋转变化而没有伸缩变化。例如, 二阶旋转矩阵 A \boldsymbol{A} A
A = [ cos θ − sin θ sin θ cos θ ] \boldsymbol{A}=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right] A = [ cos θ sin θ − sin θ cos θ ] 首先看一下旋转矩阵 A \boldsymbol{A} A i = ( 1 , 0 ) , j = ( 0 , 1 ) \boldsymbol{i}=(1,0), \boldsymbol{j}=(0,1) i = ( 1 , 0 ) , j = ( 0 , 1 )
A i = [ cos θ − sin θ sin θ cos θ ] ( 1 0 ) = ( cos θ sin θ ) \begin{gathered}
\boldsymbol{A i}=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\binom{1}{0}=\binom{\cos \theta}{\sin \theta} \\
\end{gathered} Ai = [ cos θ sin θ − sin θ cos θ ] ( 0 1 ) = ( sin θ cos θ ) \quad
A j = [ cos θ − sin θ sin θ cos θ ] ( 0 1 ) = ( − sin θ cos θ ) = ( cos ( θ + π / 2 ) sin ( θ + π / 2 ) ) \begin{gathered}
\boldsymbol{A j}=\left[\begin{array}{cc}
\cos \theta & -\sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]\binom{0}{1}=\binom{-\sin \theta}{\cos \theta}=\binom{\cos (\theta+\pi / 2)}{\sin (\theta+\pi / 2)}
\end{gathered} Aj = [ cos θ sin θ − sin θ cos θ ] ( 1 0 ) = ( cos θ − sin θ ) = ( sin ( θ + π /2 ) cos ( θ + π /2 ) ) 再结合下图, 可以看出, 旋转矩阵对单位向量 i 、 j \boldsymbol{i} 、 \boldsymbol{j} i 、 j θ \theta θ A i A i A i A j A j A j i → A i i \rightarrow A i i → A i θ \theta θ j → A j \boldsymbol{j} \rightarrow \boldsymbol{A} \boldsymbol{j} j → A j θ \theta θ
然后, 我们考察旋转矩阵 A \boldsymbol{A} A c \boldsymbol{c} c A c \boldsymbol{A} \boldsymbol{c} A c c \boldsymbol{c} c
c = ( c 1 c 2 ) = c 1 ( 1 0 ) + c 2 ( 0 1 ) = c 1 i + c 2 j \boldsymbol{c}=\binom{c_1}{c_2}=c_1\binom{1}{0}+c_2\binom{0}{1}=c_1 \boldsymbol{i}+c_2 \boldsymbol{j} c = ( c 2 c 1 ) = c 1 ( 0 1 ) + c 2 ( 1 0 ) = c 1 i + c 2 j 那么, 旋转矩阵作用于向量 c \boldsymbol{c} c
A c = A ( c 1 ( 1 0 ) + c 2 ( 0 1 ) ) = c 1 A ( 1 0 ) + c 2 A ( 0 1 ) = c 1 A i + c 2 A j \boldsymbol{A} \boldsymbol{c}=\boldsymbol{A}\left(c_1\binom{1}{0}+c_2\binom{0}{1}\right)=c_1 \boldsymbol{A}\binom{1}{0}+c_2 \boldsymbol{A}\binom{0}{1}=c_1 \boldsymbol{A} \boldsymbol{i}+c_2 \boldsymbol{A} \boldsymbol{j} A c = A ( c 1 ( 0 1 ) + c 2 ( 1 0 ) ) = c 1 A ( 0 1 ) + c 2 A ( 1 0 ) = c 1 A i + c 2 A j 对比上式 ,上面提到,一个向量乘以旋转矩阵A A A θ \theta θ c 1 i → c 1 A i c_1 i \rightarrow c_1 A i c 1 i → c 1 A i θ \theta θ c 2 j → c 2 A j c_2 \boldsymbol{j} \rightarrow c_2 \boldsymbol{A} \boldsymbol{j} c 2 j → c 2 A j θ \theta θ c 1 i + c 2 j → c 1 A i + c 2 A j c_1 \boldsymbol{i}+c_2 \boldsymbol{j} \rightarrow c_1 \boldsymbol{A} \boldsymbol{i}+c_2 \boldsymbol{A} \boldsymbol{j} c 1 i + c 2 j → c 1 A i + c 2 A j θ \theta θ c → A c c \rightarrow A c c → A c θ \theta θ
因此,A B = C \boldsymbol{A B = C} AB = C A \boldsymbol{A} A B \boldsymbol{B} B 旋转、缩放、镜像 等变换, 得到数个新向量, 这些新向量作为列向量组成一个新的矩阵 C \boldsymbol{C} C C \boldsymbol{C} C
计算机图形学 计算机图形是在计算机屏幕上显示或活动的图像.计算机图形学的应用广泛,发展迅速.例如,计算机辅助设计(CAD)是许多工程技术的组成部分之一,在最简单的二维图形符号中,字母用于在屏幕上做标记.某些字母作为线框对象存储,其他有弯曲部分的字母还要将曲线的数学公式也存储进去.
例 图2-15中的大写字母 N 由 8 个点组成,计算机里存储这8个点的坐标到矩阵D D D N N N
当描述这些对象的顶点被变换以后,他的图像也就跟着变换。
例 给定 A = [ 1 0.25 0 1 ] A=\left[\begin{array}{cc}1 & 0.25 \\ 0 & 1\end{array}\right] A = [ 1 0 0.25 1 ] x ↦ A x x \mapsto A x x ↦ A x
解 由矩阵乘法的定义,乘积 A D A D A D
变换过的顶点画在图 2-16,同时还画上相应于原来图形中连线的线段.
图 2-16 中斜体的 N 看来有些太宽,为此,我们可以用倍乘变换使它变窄.
例 先作如上例的剪切变换,然后再把 x x x x x x
S = [ 0.75 0 0 1 ] S=\left[\begin{array}{ll}
0.75 & 0 \\
0 & 1
\end{array}\right] S = [ 0.75 0 0 1 ] 所以复合变换的矩阵是
S A = [ 0.75 0 0 1 ] [ 1 0.25 0 1 ] = [ 0.75 0.1875 0 1 ] S A=\left[\begin{array}{ll}
0.75 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{ll}
1 & 0.25 \\
0 & 1
\end{array}\right]=\left[\begin{array}{ll}
0.75 & 0.1875 \\
0 & 1
\end{array}\right] S A = [ 0.75 0 0 1 ] [ 1 0 0.25 1 ] = [ 0.75 0 0.1875 1 ] 复合变换的结果如图 2-17 所示.
总结 通过上面的例子,我们有2个小小结论:
①微观上看,1 − 8 1-8 1 − 8 1 − 8 1-8 1 − 8
延伸阅读 反射变换 反射变换(Reflection)指的是图片对着 x 轴或者 y 轴做对称变换。对于图片上的点 ( x , y ) (x, y) ( x , y )
x ′ = − x y ′ = y \begin{gathered}
x^{\prime}=-x \\
y^{\prime}=y
\end{gathered} x ′ = − x y ′ = y 表示成矩阵形式为:
[ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ − 1 0 0 1 ] [ x y ] 同理可以得到 y 轴对称反射变换后的变换矩阵为:
[ x ′ y ′ ] = [ 1 0 0 − 1 ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ 1 0 0 − 1 ] [ x y ] 沿原点反射变换的变换矩阵为:
[ x ′ y ′ ] = [ − 1 0 0 − 1 ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ − 1 0 0 − 1 ] [ x y ] 切变变换 切变变换(Shear),指的是在物理学上指的是两个距离很近,大小相等,方向相反的平行力作用于同一物体上所引起的形变。使用示意图可以更直观的去表示什么是切变。如图2.2所示,是图片在 x 轴方向上发生了切变。从图中我们可以看出所有点在 y 轴上的坐标不变,在 x 轴上的坐标满足:y = 0 y=0 y = 0 y = 1 y=1 y = 1 a a a a y a y a y
切变的矩阵变换可以写作:
[ x ′ y ′ ] = [ 1 a 0 1 ] [ x y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
1 & a \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right] [ x ′ y ′ ] = [ 1 0 a 1 ] [ x y ] 线性变换 对于任何一种变换如果可以写作:
x ′ = a x + b y y ′ = c x + d y \begin{aligned}
& x^{\prime}=a x+b y \\
& y^{\prime}=c x+d y
\end{aligned} x ′ = a x + b y y ′ = c x + d y 矩阵形式可以表示为:
[ x ′ y ′ ] = [ a b c d ] [ x y ] x ′ = M x \begin{array}{r}
{\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]} \\
x^{\prime}=M x
\end{array} [ x ′ y ′ ] = [ a c b d ] [ x y ] x ′ = M x 那么我们认为这种变换是线性变换(Linear transformation)。
齐次坐标 平移变换 平移变换(Translation)相比于以上的线性变换有特殊的地方。平移变换的数学形式为:
x ′ = x + t x y ′ = y + t y \begin{aligned}
& x^{\prime}=x+t_x \\
& y^{\prime}=y+t_y
\end{aligned} x ′ = x + t x y ′ = y + t y 这种数学表示不能写作线性变换的矩阵形式,只能记作:
[ x ′ y ′ ] = [ a b c d ] [ x y ] + [ t x t y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]+\left[\begin{array}{l}
t_x \\
t_y
\end{array}\right] [ x ′ y ′ ] = [ a c b d ] [ x y ] + [ t x t y ] 说明平移操作不是线性变换。但是我们不希望把平移操作看作特殊变换,因此需要把这些变换统一起来,就引入了齐次坐标。
为了统一变换操作,我们引入一个新的维度。对于二维的点 ( x , y ) (x, y) ( x , y ) ( x , y , 1 ) , 2 (x, y, 1) , ~ 2 ( x , y , 1 ) , 2 ( x , y , 0 ) (x, y, 0) ( x , y , 0 )
[ x ′ y ′ w ′ ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] = [ x + t x y + t y 1 ] \left[\begin{array}{c}
x^{\prime} \\
y^{\prime} \\
w^{\prime}
\end{array}\right]=\left[\begin{array}{lll}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
1
\end{array}\right]=\left[\begin{array}{c}
x+t_x \\
y+t_y \\
1
\end{array}\right] x ′ y ′ w ′ = 1 0 0 0 1 0 t x t y 1 x y 1 = x + t x y + t y 1 为什么点补充维度大小为 1 ,但是向量补充维度大小为 0 ?
对于向量来说,平移变换不应该使向量的结果发生变化。因此补充维度为 0 的时候可以屏蔽平移带来的影响。
对于加入齐次坐标的点和向量满足:
向量 + 向量 = 向量
点-点 = 向量
点 + 向量 = 点
点 + 点 = 两个点中点
对引入齐次坐标的点的扩充定义如下:
( x y w ) = ( x / w y / w 1 ) , w ≠ 0 \left(\begin{array}{l}
x \\
y \\
w
\end{array}\right)=\left(\begin{array}{c}
x / w \\
y / w \\
1
\end{array}\right), w \neq 0 x y w = x / w y / w 1 , w = 0 仿射变换 仿射变换(Affine)包含线性变换与平移变换。可以用矩阵表示为:
[ x ′ y ′ ] = [ a b c d ] [ x y ] + [ t x t y ] \left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]+\left[\begin{array}{c}
t_x \\
t_y
\end{array}\right] [ x ′ y ′ ] = [ a c b d ] [ x y ] + [ t x t y ] 使用齐次坐标后可以写作:
[ x ′ y ′ w ′ ] = [ a b t x c d t y 0 0 1 ] [ x y 1 ] = [ a x + b y + t x c x + d y + t y 1 ] \left[\begin{array}{c}
x^{\prime} \\
y^{\prime} \\
w^{\prime}
\end{array}\right]=\left[\begin{array}{lll}
a & b & t_x \\
c & d & t_y \\
0 & 0 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
1
\end{array}\right]=\left[\begin{array}{c}
a x+b y+t_x \\
c x+d y+t_y \\
1
\end{array}\right] x ′ y ′ w ′ = a c 0 b d 0 t x t y 1 x y 1 = a x + b y + t x c x + d y + t y 1 逆变换 任何变换乘以他的逆矩阵A − 1 A^{-1} A − 1
变换的组合与分解 可以用矩阵的乘法进行变换的组合(Transform compose ® { }^{\text {® }} R ◯ A 1 , A 2 , A 3 , ⋯ A 1, ~ A 2, ~ A 3, \cdots A 1 , A 2 , A 3 , ⋯
A n ( … A 2 ( A 1 ( x ) ) ) = A n … A 2 ⋅ A 1 ⋅ ( x y 1 ) A_n\left(\ldots A_2\left(A_1(x)\right)\right)=A_n \ldots A_2 \cdot A_1 \cdot\left(\begin{array}{l}
x \\
y \\
1
\end{array}\right) A n ( … A 2 ( A 1 ( x ) ) ) = A n … A 2 ⋅ A 1 ⋅ x y 1 根据矩阵运算的结合律,我们可以先把变换矩阵乘在一起,接下来把这个矩阵的乘积和向量相乘。可以用一个矩阵表示一个复杂的变换。
变换的分解 所有的复杂变换都可以分解成多个普通的变换。为了使某个图像沿着某个点 c c c
1.把中心点 c c c ( 0 , 0 ) (0,0) ( 0 , 0 )
用变换矩阵表示为:
M t ( c ) ⋅ M r ( θ ) ⋅ M t ( − c ) M_t(c) \cdot M_r(\theta) \cdot M_t(-c) M t ( c ) ⋅ M r ( θ ) ⋅ M t ( − c )
三维变换 3 维变换可以类比于 2 维变换得到引入齐次坐标的点和向量, 3 维的点可以表示为 ( x , y , z , 1 ) T (x, y, z, 1) T ( x , y , z , 1 ) T ( x , y , z , 0 ) T (x, y, z, 0) T ( x , y , z , 0 ) T w w w ≠ 0 \neq 0 = 0 ( x , y , z , w ) = ( x / w , y / w , z / w , 1 ) (x, y, z, w)=(x / w, y / w, z / w, 1) ( x , y , z , w ) = ( x / w , y / w , z / w , 1 )
使用 4 × 4 4 \times 4 4 × 4
( x ′ y ′ z ′ 1 ) = ( a b c t x d e f t y g h i t z 0 0 0 1 ) ⋅ ( x y z 1 ) \left(\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime} \\
1
\end{array}\right)=\left(\begin{array}{llll}
a & b & c & t_x \\
d & e & f & t_y \\
g & h & i & t_z \\
0 & 0 & 0 & 1
\end{array}\right) \cdot\left(\begin{array}{l}
x \\
y \\
z \\
1
\end{array}\right) x ′ y ′ z ′ 1 = a d g 0 b e h 0 c f i 0 t x t y t z 1 ⋅ x y z 1 左上角表示是一个 3 × 3 3 \times 3 3 × 3
1. 3 维变换中缩放变换
3 维变换中缩放变换的变换矩阵:
S ( s x , s y , s z ) = ( s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ) S \left(s_x, s_y, s_z\right)=\left(\begin{array}{cccc}
s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1
\end{array}\right) S ( s x , s y , s z ) = s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 2.维变换中的平移变换
三维变换中平移变换的变换矩阵:
T ( t x , t y , t z ) = ( 1 0 0 t x 0 1 0 t y 0 0 1 t z 0 0 0 1 ) T \left(t_x, t_y, t_z\right)=\left(\begin{array}{cccc}
1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1
\end{array}\right) T ( t x , t y , t z ) = 1 0 0 0 0 1 0 0 0 0 1 0 t x t y t z 1 3.三维变换中的旋转变换
当空间内的物体绕着 x x x y y y z z z
R x ( α ) = ( 1 0 0 0 0 cos α − sin α 0 0 sin α cos α 0 0 0 0 1 ) R y ( α ) = ( cos α 0 sin α 0 0 1 0 0 − sin α 0 cos α 0 0 0 0 1 ) \begin{aligned}
& R _x(\alpha)=\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & \cos \alpha & -\sin \alpha & 0 \\
0 & \sin \alpha & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{array}\right) \\
& R _y(\alpha)=\left(\begin{array}{cccc}
\cos \alpha & 0 & \sin \alpha & 0 \\
0 & 1 & 0 & 0 \\
-\sin \alpha & 0 & \cos \alpha & 0 \\
0 & 0 & 0 & 1
\end{array}\right)
\end{aligned} R x ( α ) = 1 0 0 0 0 cos α sin α 0 0 − sin α cos α 0 0 0 0 1 R y ( α ) = cos α 0 − sin α 0 0 1 0 0 sin α 0 cos α 0 0 0 0 1 R z ( α ) = ( cos α − sin α 0 0 sin α cos α 0 0 0 0 1 0 0 0 0 1 ) R _z(\alpha)=\left(\begin{array}{cccc}
\cos \alpha & -\sin \alpha & 0 & 0 \\
\sin \alpha & \cos \alpha & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{array}\right) R z ( α ) = cos α sin α 0 0 − sin α cos α 0 0 0 0 1 0 0 0 0 1 CSDN@搬砖怪
对于一般性的旋转问题,可以用简单的旋转描述复杂的旋转。用 x x x y y y z z z
R x y z ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ ) R _{x y z}(\alpha, \beta, \gamma)= R _x(\alpha) R _y(\beta) R _z(\gamma) R x yz ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ ) CSDN@恻砖怪
这三个角就被称作欧拉角(Euler angles)。
更多介绍请参考CSDN此处
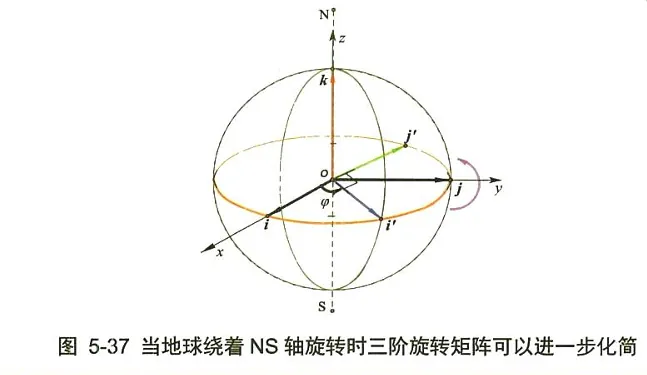
三维旋转 { ( cos θ cos φ , cos θ sin φ , − sin θ ) T , ( − sin φ , cos φ , 0 ) T , ( sin θ cos φ , sin θ sin φ , cos θ ) T } \left\{(\cos \theta \cos \varphi, \cos \theta \sin \varphi,-\sin \theta)^{T},(-\sin \varphi, \cos \varphi, 0)^{T},(\sin \theta \cos \varphi, \sin \theta \sin \varphi, \cos \theta)^{T}\right\} { ( cos θ cos φ , cos θ sin φ , − sin θ ) T , ( − sin φ , cos φ , 0 ) T , ( sin θ cos φ , sin θ sin φ , cos θ ) T } ( 0 ⩽ θ ⩽ π , 0 ⩽ φ ⩽ 2 π ) (0 \leqslant \theta \leqslant \pi, 0 \leqslant \varphi \leqslant 2 \pi) ( 0 ⩽ θ ⩽ π , 0 ⩽ φ ⩽ 2 π ) x , y , z x, ~ y, ~ z x , y , z
[ cos θ cos φ − sin φ sin θ cos φ cos θ sin φ cos φ sin θ sin φ − sin θ 0 cos θ ] \left[\begin{array}{ccc}
\cos \theta \cos \varphi & -\sin \varphi & \sin \theta \cos \varphi \\
\cos \theta \sin \varphi & \cos \varphi & \sin \theta \sin \varphi \\
-\sin \theta & 0 & \cos \theta
\end{array}\right] cos θ cos φ cos θ sin φ − sin θ − sin φ cos φ 0 sin θ cos φ sin θ sin φ cos θ 在图 5-37 中,如果我们取定地球自转的旋转轴为 z z z z z z θ = 0 \theta=0 θ = 0 φ \varphi φ x x x i i i φ \varphi φ y y y j j j φ \varphi φ z z z k k k φ = 0 \varphi=0 φ = 0 A : A : A :
A = [ cos φ − sin φ 0 sin φ cos φ 0 0 0 1 ] A =\left[\begin{array}{ccc}
\cos \varphi & -\sin \varphi & 0 \\
\sin \varphi & \cos \varphi & 0 \\
0 & 0 & 1
\end{array}\right] A = cos φ sin φ 0 − sin φ cos φ 0 0 0 1
在计算 A A A
注意有几个例外。当 φ \varphi φ 180 ∘ 180^{\circ} 18 0 ∘ 180 ∘ 180^{\circ} 18 0 ∘ B B B
B = [ cos φ − sin φ 0 sin φ cos φ 0 0 0 1 ] ∣ φ = π = [ − 1 0 0 0 − 1 0 0 0 1 ] B =\left.\left[\begin{array}{ccc}
\cos \varphi & -\sin \varphi & 0 \\
\sin \varphi & \cos \varphi & 0 \\
0 & 0 & 1
\end{array}\right]\right|_{\varphi=\pi}=\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 1
\end{array}\right] B = cos φ sin φ 0 − sin φ cos φ 0 0 0 1 φ = π = − 1 0 0 0 − 1 0 0 0 1 别走,还有特征向量没找完呢。当你继续旋转地球到 360 ∘ 360^{\circ} 36 0 ∘ 360 ∘ 360^{\circ} 36 0 ∘ C C C
C = [ cos φ − sin φ 0 sin φ cos φ 0 0 0 1 ] ∣ φ = 2 π = [ 1 0 0 0 1 0 0 0 1 ] = E C =\left.\left[\begin{array}{ccc}
\cos \varphi & -\sin \varphi & 0 \\
\sin \varphi & \cos \varphi & 0 \\
0 & 0 & 1
\end{array}\right]\right|_{\varphi=2 \pi}=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]= E C = cos φ sin φ 0 − sin φ cos φ 0 0 0 1 φ = 2 π = 1 0 0 0 1 0 0 0 1 = E 原来把所有向量整成特征向量的矩阵不是别人,正是大名鼎鼎的单位矩阵 E E E ∣ A − λ E ∣ = 0 | A -\lambda E |=0 ∣ A − λ E ∣ = 0
λ 1 = 1 , λ 2 = cos φ + i sin φ , λ 3 = cos φ − i sin φ \lambda_1=1, \lambda_2=\cos \varphi+i \sin \varphi, \lambda_3=\cos \varphi-i \sin \varphi λ 1 = 1 , λ 2 = cos φ + i sin φ , λ 3 = cos φ − i sin φ 出现复数的特征值了。高中我们就学过,一个数乘以复数i i i
当 λ 1 = 1 \lambda_1=1 λ 1 = 1 φ \varphi φ k ( 0 0 1 ) k\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) k 0 0 1 z z z φ \varphi φ 360 ∘ 360^{\circ} 36 0 ∘ E E E k 1 ( 1 0 0 ) + k 2 ( 0 1 0 ) + k 3 ( 0 0 1 ) k_1\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)+k_2\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right)+k_3\left(\begin{array}{l}0 \\ 0 \\ 1\end{array}\right) k 1 1 0 0 + k 2 0 1 0 + k 3 0 0 1
当 λ 1 = − 1 \lambda_1=-1 λ 1 = − 1 φ = π \varphi=\pi φ = π k 1 ( 1 0 0 ) + k 2 ( 0 1 0 ) k_1\left(\begin{array}{l}1 \\ 0 \\ 0\end{array}\right)+k_2\left(\begin{array}{l}0 \\ 1 \\ 0\end{array}\right) k 1 1 0 0 + k 2 0 1 0
 {width=600px}
{width=600px}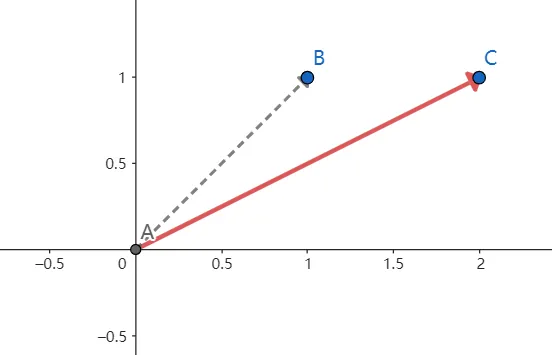 {width=300px}
{width=300px}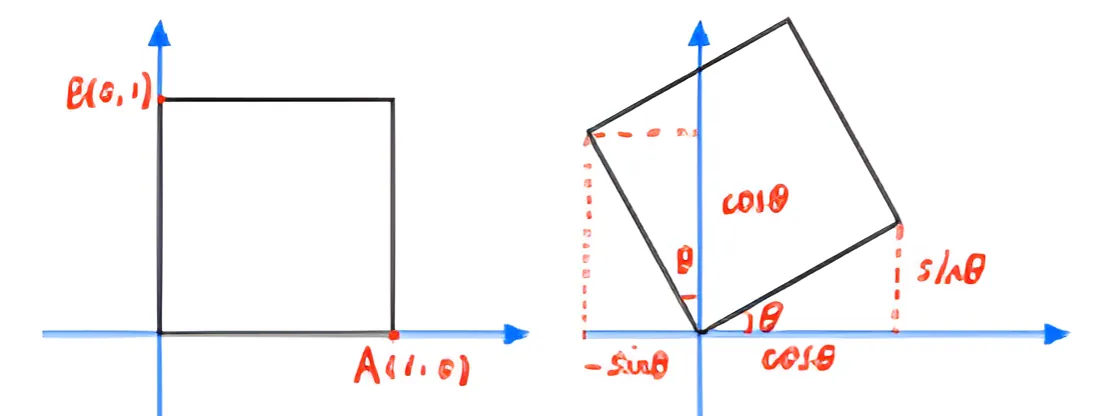 {width=500px}
{width=500px}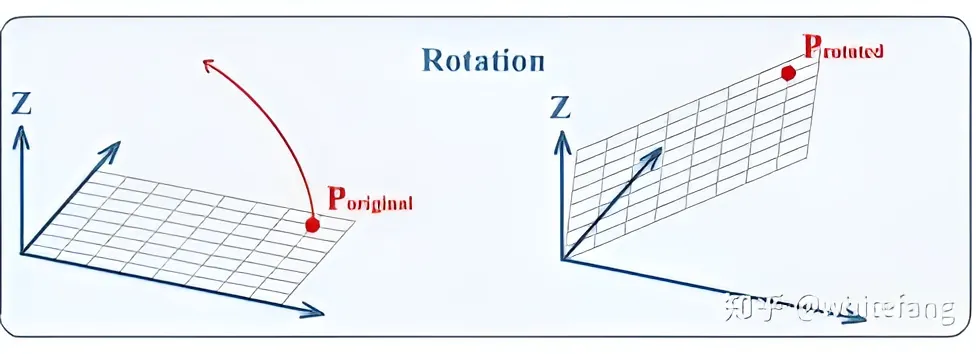 {width=600px}
{width=600px}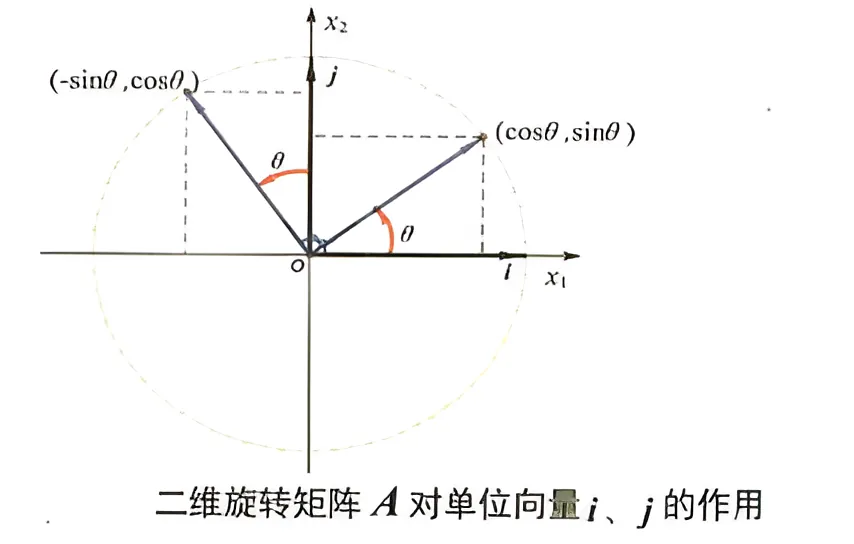 {width=600px}
{width=600px}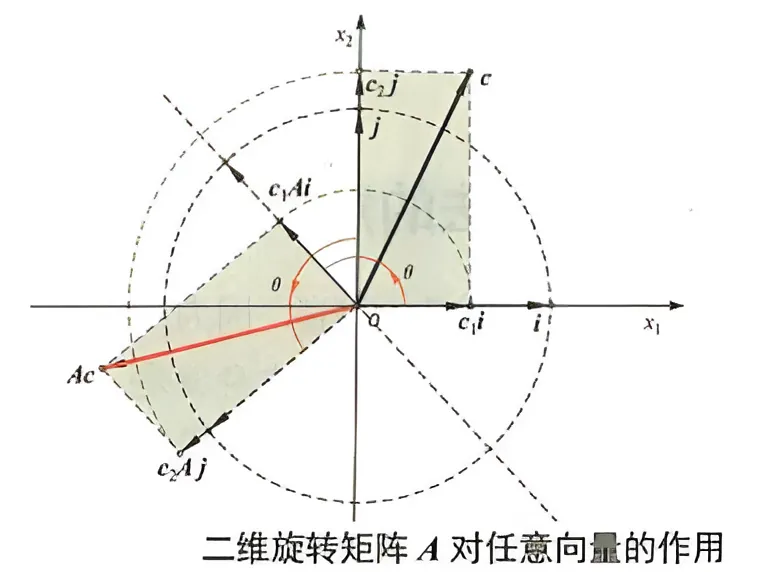 {width=600px}
{width=600px}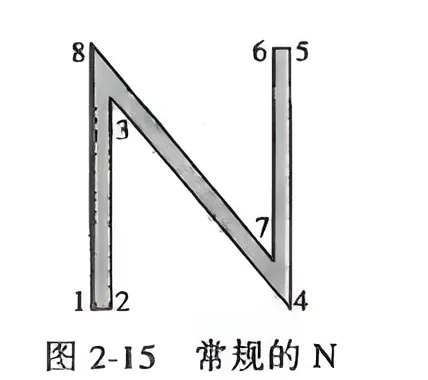 {width=300px}
{width=300px}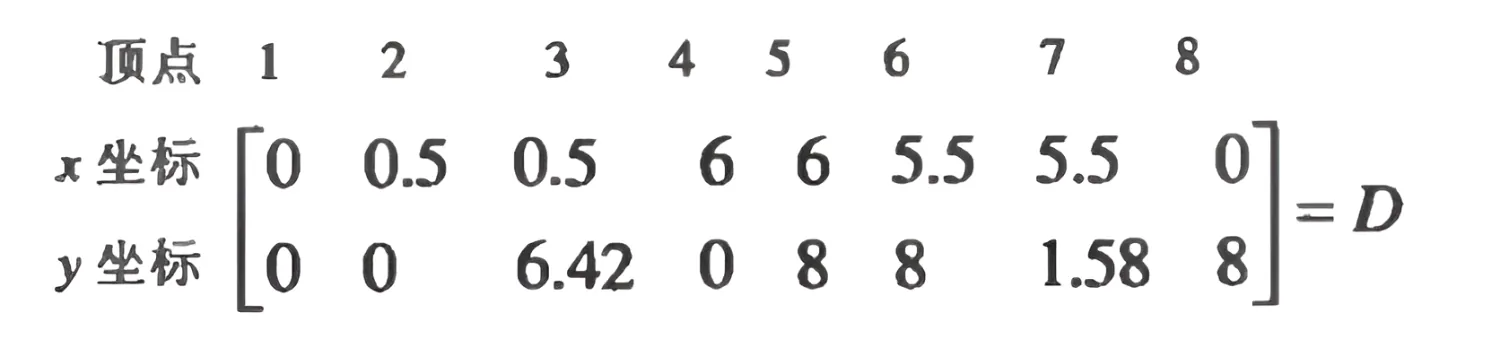 {width=550px}
{width=550px}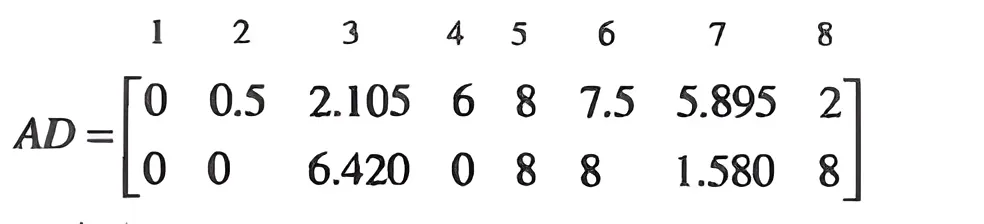 {width=550px}
{width=550px}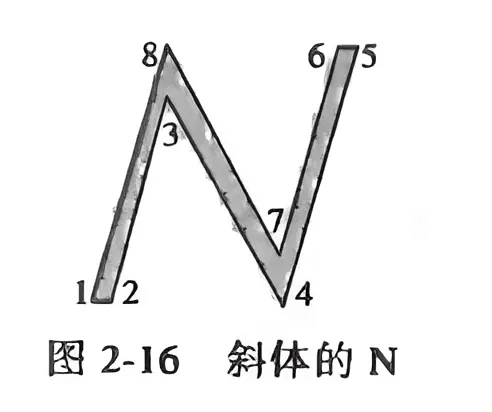 {width=300px}
{width=300px} {width=300px}
{width=300px} {width=500px}
{width=500px}