15._方程组解的判定

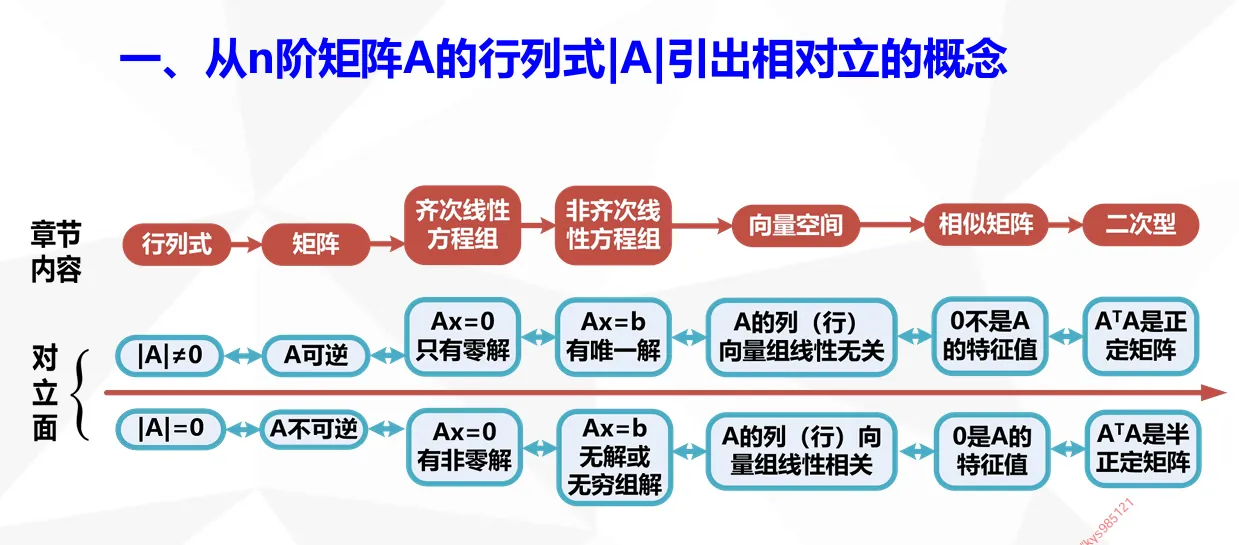
方程组解的判定

克莱姆法则(以二阶为例) 对于二阶线性方程组: {a1x+b1y=c1a2x+b2y=c2\left\{\begin{array}{l}a_1 x+b_1 y=c_1 \\ a_2 x+b_2 y=c_2\end{array}\right., 其克莱姆法则的解为

x=∣c1b1c2b2∣∣a1b1a2b2∣,y=∣a1c1a2c2∣∣a1b1a1b2∣x=\frac{\left|\begin{array}{ll} c_1 & b_1 \\ c_2 & b_2 \end{array}\right|}{\left|\begin{array}{ll} a_1 & b_1 \\ a_2 & b_2 \end{array}\right|}, y=\frac{\left|\begin{array}{ll} a_1 & c_1 \\ a_2 & c_2 \end{array}\right|}{\left|\begin{array}{ll} a_1 & b_1 \\ a_1 & b_2 \end{array}\right|}

仔细观察方程解的分母，他就是系数行列式，

∣A∣=∣a1b1a1b2∣|A|=\left|\begin{array}{ll} a_1 & b_1 \\ a_1 & b_2 \end{array}\right|

因此，我们得到第一个定理：

定理1 如果线性方程组 AX=βA X=\beta 的系数行列式不等于零，且解是唯一的。

定理2 如果线性方程组 AX=βA X=\beta 无解或无穷多解，则它的系数行列式必等于零， 即 ∣A∣=0|A|=0.

定理1和定理2反应了 行列式和方程解的对立。通俗的说：就是和你对着干。 行列式的值不为零，我就有解。 行列式的值是零，我就无解或无穷解。

完理3 如果齐次线性方程组 AX=0A X=0 的系数行列式不等于零，即 ∣A∣∣≠0|A| \mid \neq 0 ，则它只零解 x1=x2=⋯=xn=0x_1=x_2=\cdots=x_n=0.

定理4 如果齐次线性方程组 AX=0A X=0 有非零解，则必有它的系数行列式等于零， 即 ∣A∣=0|A|=0.

定理3和定理4也反应了 行列式和方程解的对立。 行列式的值非零，我就只有零解。 行列式的值是为零，我有非零解。

例如

{x+y=22x+2y=4\left\{\begin{array}{l} x+y=2\\ 2 x+ 2 y=4\end{array}\right.

方程系数成比例， 因此行列式等于零，有无穷多解。

方程解的判定见下表，完整介绍点击 此处

img-text

例题

行列式提供了对方程解的判断。请看下面例题。换句话说，对方程组的求解压力转移到行列式的计算上。

例问 λ\lambda 取何值时，下面的齐次线性方程组有非零解?

{λx1+x2+3x3=0x1+(λ−1)x2+x3=0x1+x2+(λ−1)x3=0\left\{\begin{array}{l} \lambda x_1+x_2+3 x_3=0 \\ x_1+(\lambda-1) x_2+x_3=0 \\ x_1+x_2+(\lambda-1) x_3=0 \end{array}\right.

解 若所给齐次线性方程组有非零解，则它的系数行列式 ∣A∣=0|A|=0. 即

∣A∣=∣λ131λ−1111λ−1∣=∣λ131λ−1102−λλ−2∣=∣λ141λ−1λ02−λ0∣=(2−λ)(−1)3+2∣λ41λ∣=(λ−2)2(λ+2)=0|\boldsymbol{A}|=\left|\begin{array}{ccc} \lambda & 1 & 3 \\ 1 & \lambda-1 & 1 \\ 1 & 1 & \lambda-1 \end{array}\right|=\left|\begin{array}{ccc} \lambda & 1 & 3 \\ 1 & \lambda-1 & 1 \\ 0 & 2-\lambda & \lambda-2 \end{array}\right|=\left|\begin{array}{ccc} \lambda & 1 & 4 \\ 1 & \lambda-1 & \lambda \\ 0 & 2-\lambda & 0 \end{array}\right|=(2-\lambda)(-1)^{3+2}\left|\begin{array}{cc} \lambda & 4 \\ 1 & \lambda \end{array}\right|=(\lambda-2)^2(\lambda+2)=0

所以当 λ=−2\lambda=-2 或 λ=2\lambda=2 时，该齐次线性方程组有非零解.

例 设 a,b,c,da, b, c, d 为不全为零的实数，证明下面齐次线性方程组只有零解：

{ax1+bx2+cx3+dx4=0bx1−ax2+dx3−cx4=0cx1−dx2−ax3+bx4=0dx1+cx2−bx3−ax4=0\left\{\begin{array}{l} a x_1+b x_2+c x_3+d x_4=0 \\ b x_1-a x_2+d x_3-c x_4=0 \\ c x_1-d x_2-a x_3+b x_4=0 \\ d x_1+c x_2-b x_3-a x_4=0 \end{array}\right.

证明：系数矩阵 A=(abcdb−ad−cc−d−abdc−b−a)\boldsymbol{A}=\left(\begin{array}{rrrr}a & b & c & d \\ b & -a & d & -c \\ c & -d & -a & b \\ d & c & -b & -a\end{array}\right) ，注意到 ∣A∣|\boldsymbol{A}| 不方便化到三角行列式，

考虑 AT=(abcdb−a−dccd−a−bd−cb−a)\boldsymbol{A}^{\mathrm{T}}=\left(\begin{array}{rrrr}a & b & c & d \\ b & -a & -d & c \\ c & d & -a & -b \\ d & -c & b & -a\end{array}\right) ，有

AAT=diag⁡(a2+b2+c2+d2,a2+b2+c2+d2,a2+b2+c2+d2,a2+b2+c2+d2)\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}=\boldsymbol{\operatorname { d i a g }}\left(a^2+b^2+c^2+d^2, a^2+b^2+c^2+d^2, a^2+b^2+c^2+d^2, a^2+b^2+c^2+d^2\right)

因为 a,b,c,da, b, c, d 不全为 0 ，所以

∣A∣∣AT∣=∣AAT∣=(a2+b2+c2+d2)4≠0. |\boldsymbol{A}|\left|\boldsymbol{A}^{\mathrm{T}}\right|=\left|\boldsymbol{A} \boldsymbol{A}^{\mathrm{T}}\right|=\left(a^2+b^2+c^2+d^2\right)^4 \neq 0 \text {. }

从而 ∣A∣≠0|\boldsymbol{A}| \neq 0 ，由推论知原齐次线性方程组只有零解．

例 讨论当 μ\mu 取何值时，线性方程组

{(μ−1)x1+3x2−2x3=1,x1+(μ+1)x2−2x3=1,5x1−x2+(μ−4)x3=−3\left\{\begin{aligned} (\mu-1) x_1+3 x_2- & 2 x_3=1, \\ x_1+(\mu+1) x_2- & 2 x_3=1, \\ 5 x_1- & x_2+(\mu-4) x_3=-3 \end{aligned}\right.

有无穷多解，并求其通解． 解 该线性方程组的系数行列式

∣A∣=∣μ−13−21μ+1−25−1μ−4∣=r1−r2∣μ−2−μ+201μ+1−25−1μ−4∣=c2+c1∣μ−2001μ+2−254μ−4∣=(μ−2)∣μ+2−24μ−4∣=μ(μ−2)2.\begin{aligned} & |A|=\left|\begin{array}{ccc} \mu-1 & 3 & -2 \\ 1 & \mu+1 & -2 \\ 5 & -1 & \mu-4 \end{array}\right| \xlongequal{r_1-r_2}\left|\begin{array}{ccc} \mu-2 & -\mu+2 & 0 \\ 1 & \mu+1 & -2 \\ 5 & -1 & \mu-4 \end{array}\right| \\ & \xlongequal{c_2+c_1}\left|\begin{array}{ccc} \mu-2 & 0 & 0 \\ 1 & \mu+2 & -2 \\ 5 & 4 & \mu-4 \end{array}\right|=(\mu-2)\left|\begin{array}{cc} \mu+2 & -2 \\ 4 & \mu-4 \end{array}\right|=\mu(\mu-2)^2 . \end{aligned}

由于方程组有无穷多解，故 ∣A∣=0|\boldsymbol{A}|=0 ，即 μ=0\mu=0 或 μ=2\mu=2 ． 当 μ=0\mu=0 时，对方程组的增广矩阵 A~\tilde{\boldsymbol{A}} 作初等行变换后化为行阶梯形矩阵，

A~=[−13−2111−215−1−4−3]→[11−2104−42000−5]\tilde{\boldsymbol{A}}=\left[\begin{array}{rrr:r} -1 & 3 & -2 & 1 \\ 1 & 1 & -2 & 1 \\ 5 & -1 & -4 & -3 \end{array}\right] \rightarrow\left[\begin{array}{rrr:r} 1 & 1 & -2 & 1 \\ 0 & 4 & -4 & 2 \\ 0 & 0 & 0 & -5 \end{array}\right]

此时 r(A)≠r(A~)r(\boldsymbol{A}) \neq r(\tilde{\boldsymbol{A}}) ，方程组无解，即 μ=0\mu=0 不满足题设条件，舍去． 当 μ=2\mu=2 时，对方程组的增广矩阵 A~\tilde{\boldsymbol{A}} 作初等行变换后化为行阶梯形矩阵，

A~=[13−2113−215−1−2−3]→[13−210−21−10000]→[10−12−1201−12120000].\tilde{\boldsymbol{A}}=\left[\begin{array}{rrr:r} 1 & 3 & -2 & 1 \\ 1 & 3 & -2 & 1 \\ 5 & -1 & -2 & -3 \end{array}\right] \rightarrow\left[\begin{array}{rrr:r} 1 & 3 & -2 & 1 \\ 0 & -2 & 1 & -1 \\ 0 & 0 & 0 & 0 \end{array}\right] \rightarrow\left[\begin{array}{rrr:r} 1 & 0 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & 1 & -\frac{1}{2} & \frac{1}{2} \\ 0 & 0 & 0 & 0 \end{array}\right] .

此时 r(A)=r(A~)=2<3r(\boldsymbol{A})=r(\tilde{\boldsymbol{A}})=2<3 ，方程组有无穷多解．原方程组的同解方程组为

{x1=12x3−12x2=12x3+12\left\{\begin{array}{l} x_1=\frac{1}{2} x_3-\frac{1}{2} \\ x_2=\frac{1}{2} x_3+\frac{1}{2} \end{array}\right.

取 x3x_3 为自由变量，则该方程组的通解为

[x1x2x3]=[−12120]+k[12121],\left[\begin{array}{l} x_1 \\ x_2 \\ x_3 \end{array}\right]=\left[\begin{array}{r} -\frac{1}{2} \\ \frac{1}{2} \\ 0 \end{array}\right]+k\left[\begin{array}{c} \frac{1}{2} \\ \frac{1}{2} \\ 1 \end{array}\right],

其中 kk 为任意常数．

上一章14._克莱默Cramer法则
下一章16._拉普拉斯定理_Laplace