向量组的秩和极大无关组的几何意义
本节内容可以简单概括为:给我一组向量,我要选取哪几个向量来构建坐标系。
假设给我一个向量组,我希望构建一个坐标系,如何快速选择向量是个棘手问题。例如
a1=[1,0,0],a2=[0,2,0],a3=[0,0,1],a4=[0,0,5]
每个向量可以看成三维空间里的一个分量,如果我选择
a1,a2,a3 可以构建三维坐标系
a1,a2,a4 也可以构建三维坐标系
但是选择 a2,a3,a4 则不行,很明显 a3,a4 在一条直线上,他和a2 构成了一个平面,无法张成三维空间。
因此,本节我们主要解决的问题是:给你一组向量,如何找到最大的一组向量组,他可以表示向量组里的每一个向量,这就是极大无关组的意思。
在上面例子里a1,a2,a3,a4 这四个向量,要完整的表达组里的每个向量,只要3个向量就可以了,可以选择 a1,a2,a3 也可以选择 a1,a2,a4。 这表明,极大向量组的表达方式不是唯一的,但是不管怎么选,都的3个向量,所以,个数是唯一的,这个“个数”就是向量组的秩,也是空间的维数。
我们将从维度(也叫做坐标系或者叫做基)来理解线性相关与无关的意思,为此再次回顾一下坐标系的组成。
1. R1坐标系
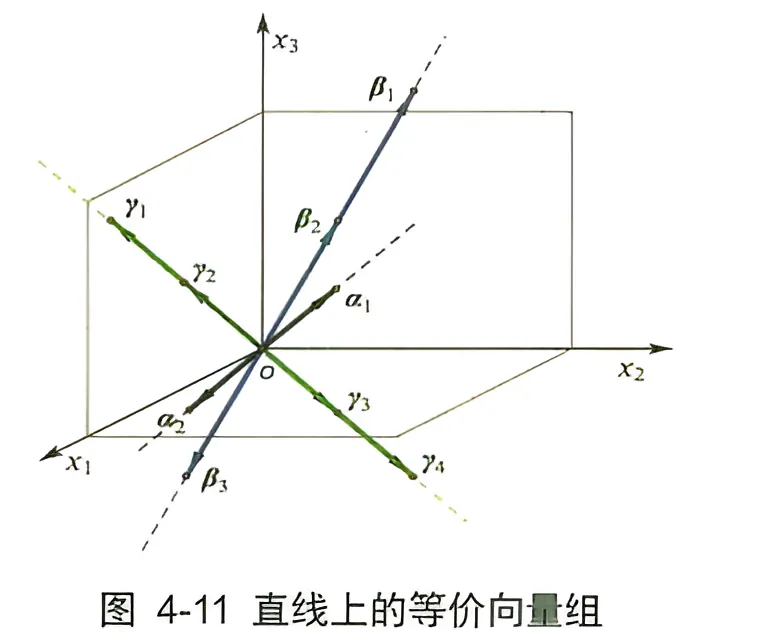
在一维坐标系里,只要a不为0,都可以当做“基”。 比如下图空间如图 4-11 所示的三维空间中, 共有三条分离的不共面直线, 每条直线上分别有两个、三个和四个向量。两向量 α1、α2 在一条直线上; 三向量 β1、β2、β3 在另外一条直线上; 四向量 γ1、γ2、γ3、γ4 在第三条直线上。任选一个向量都可以作为基。(不过,因为一维表示一个直线,所以βi向量无法表示αi和γi)
假设有三个向量 β1=(1,1,1),β2=(2,2,2),β3=(−1,−1,−1) ,这三个向量组成了一个向量组
β=(β1,β2,β3) 不难发现,人选一个而且只需要一个向量都可以作为基,所以一维的比较简单。进一步可以发现,这个向量组β的秩为1,由此得到下面结论:
对于n个向量组成的向量组,如果向量组的秩为1,表示这n个向量共线,反之也成立
 {width=500px}
{width=500px}
2. R2坐标系
在二维坐标系里,任何不重合的向量都可以作为坐标系。但是我们常用的是笛卡尔坐标系,即e1=(1,0)和e2=(0,1)
请务必牢记:笛卡尔坐标仅是一个特殊的坐标系,如果使用x=(2,4) 和 y=(3,1) 也可以作为坐标系。
上面结论,高中我们就知道了,我们要把思维进一步发散,要放的更开,我们在 集合论与向量空间 曾经说过, n维向量就像是一个枝繁叶茂的大树所构成的一个庞大物理空间 (枝繁叶茂这个词用的很好,整个向量空间想一颗参天大树,但是共用树根)。为了方便理解,我们以3维空间为例。在3维向量空间这所大房子里又可以划分出好多居室,每个居室里的向量们也严格坚守着自己居室的同样的两项基本原则:相加和缩放不能超出自己的居室, 这些大大小小的居室就是子空间。
需要注意的是, 这些居室有个特点, 就是共有一个原点, 或者说都要包括零向量。参考下图
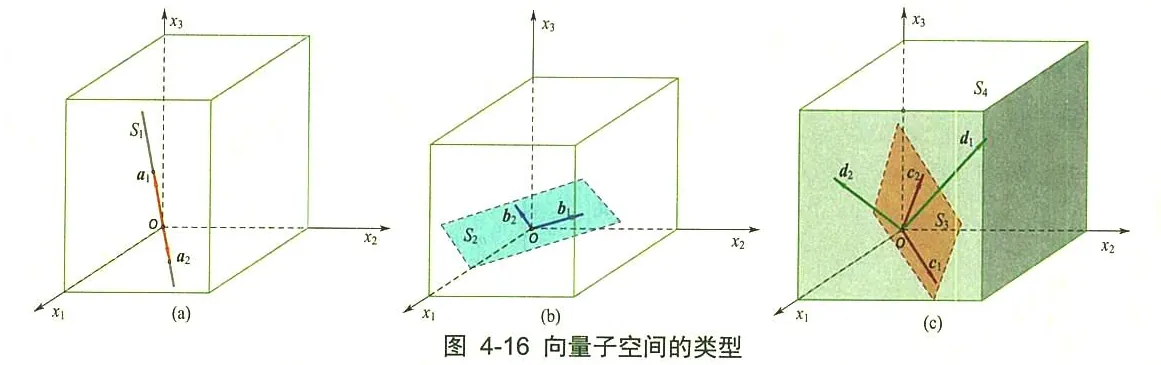
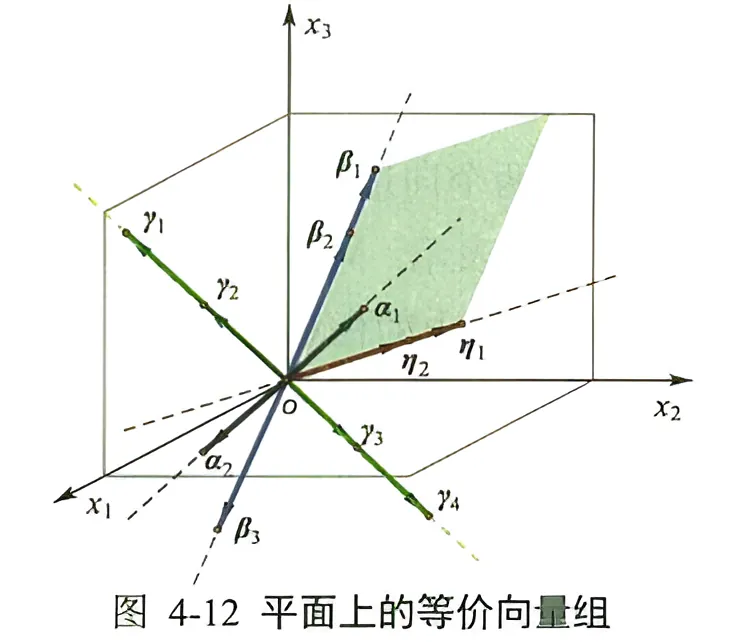
有了上面的理解, 我们看看平面上的向量组之间的等价关系。如图 4-12 所示, 向量 αi、βi、ηi 分别所在的三条直线共一平面 (阴影平行四边形), 因此向量 αi、βi、ηi 中的任何一类可以被其他两类线性表示, 例如有关系 αi=x1βi+x2ηi 。
 {width=500px}
{width=500px}
为方便理解,我们使用具体数字说明,设
α1=123,β1=456;η1=6912; 这里 η1=2α1+β1 , 从向量平行四边形法则上来说 α1 得2倍与 β1的1倍进行合成,形成了η1 ,所以这3个向量共面。如果写成矩阵,可以发现他的秩为2
B=1234566912 由此,我们可以得到第二个结论
假设给你n个向量,如果这 n 个向量的秩为2,就表示这n个向量在一个平面内。反之也成立。
3. R3坐标
在三维坐标系里,任何不重线且不重面的3向量都可以作为坐标系。 参考图4-12, 我们可以发现,在α,β,γ,η 四个家族向量组里,任取3个向量,都可以组成向量空间。
可以取 α1,β1,γ1,也可以取 α2,β1,γ1,但是取 α1,α2,γ1 不行。总之,可以有如下结论
假设给你n个向量,如果这 n 个向量的秩为3,就表示这n个向量组成一个立方体,反之也成立
 {width=500px}
{width=500px}
Rn空间
把上面推广到n维,就变成了n维空间。
如何求极大线性无关组
回到我们最原始的需求:给你一组向量,如何找到一组基呢?
假设给你一组向量 A=(a1,a2,a3,a4) 其中
a1=[1,0,0],a2=[0,2,0],a3=[0,0,1],a4=[0,0,5]
如果找到A里的一组极大向量组呢?我们可以这样思考
从几何意义上讲, 在一个向量组里, 如果有多个向量在一条直线上, 那么直线上这些向量只要一个向量就可以了, 其他的同直线的向量可以被代表了。这个向量代表可以是直线上任意一个非零向量; 进而, 如果向量组里还有多个向量构成或存在于一个平面上, 那么只要有两个非零非共线的向量就可以代表其他的共面向量了; 继续, 如果向量组里还有多个向量构成或存在于一个立体空间里, 那么只要有三个非零非共线非共面的向量就可以代表其他的同立体向量了......
所以, 一个 n 维向量组可以通过几何意义上笕选得到一个极大无关向量组, 筛选的过程可以这样:
(1)把共线的向量全部找出来; 然后对每一个直线, 各留一个向量代表, 线上其余向量删除。
(2)把上述精简后的向量组里所有共面的向量全部找出来, 然后对一个平面, 各留两个向量, 面上其余的向量删除;
(3)把上述精简后的向量组里所有共立方体的向量全部找出来, 然后对每一个立方体, 各留三个向量, 立方体内其余的向量删除;
(4)把上述精简后的向量组里所有共超立方体 ( n−1 维) 的向量全部找出来, 然后对每一个超立方体, 各留 n−1 个向量, 超立方体内其余的向量删除;
(5)留下的向量数小于等于 n, 筛选结束, 剩下的向量则为极大无关向量组。
具体操作读者可以自己线下验证。当然这种思考方式适合计算机处理,所以,我们还是从数学角度分析。
极大线性无关组的定义与性质
极大线下无关组的定义 设向量组 I: α1,α2,⋯,αm,⋯(向量个数可有限也可无限),若存在它的部分向量组 II: αi1,αi2,⋯,αi1满足:
(1) αi1,αi2,⋯,αir 线性无关;
(2)向量组 I 中的每一个向量都可由向量组 II 线性表示,则称向量组 II:αi1,αi2,⋯,αi1 是向量组 I 的一个极大线性无关组,简称极大无关组.
例如,观察向量组 α1=(1,2,−1),α2=(2,−3,1),α3=(4,1,−1) ,有 2α1+α2−α3=0 ,所以它们线性相关,而它的部分向量组 α1,α2 线性无关,向量组中的任意向量都可以由 α1,α2线性表示,即
α1=1α1+0α2,α2=0α1+1α2,α3=2α1+1α2. 同样, α2,α3 与 α1,α3 也都具有这样的性质,因此 α1,α2;α2,α3与 α1,α3 都是它的极大无关组,由此可见,向量组的极大无关组可以不唯一.
一个向量组若有极大线性无关组,则这个向量组与其极大线性无关组等价.
若向量组的极大线性无关组不唯一,则其任意两个极大线性无关组都等价.
例如,上面提到的向量组 α1=(1,2,−1),α2=(2,−3,1) , α3=(4,1,−1) 中,极大无关组有 3 个,显然,向量组 α1,α2 , α3 与 α1,α2 等价,极大无关组 α1,α2 与 α2,α3 及 α1,α3 都等价.
定理 给定两个向量组
I :α1,α2,⋯,αs, II :β1,β2,⋯,βv 若向量组 I 能被向量组 II 线性表示,且 s>t ,则向量组 I 中的向量线性相关.
证明:略
推论1 若向量 α1,α2,⋯,αs 线性无关,且它们可由向量组 β1 , β2,⋯,β ,线性表示,则 s⩽t .
推论2 两个线性无关的等价向量组必含相同个数的向量.
推论3 一个向量组若有两个极大线性无关组,则它们所含向量的个数相等.
两个容易出错的概念
例若向量组 {α1,α2,α3} 中的向量两两线性无关, 则 {α1,α2,α3} 线性无关,是否正确?
解:这个说法是错误的。可以用二维空间的向量即可证明。
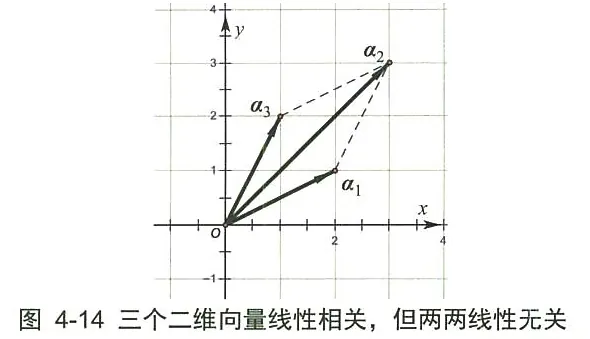
如图 4-14 所示, 向量组 {α1,α2,α3} 的向量定义如下: α1=(2,1),α2=(3,3),α3=(1,2),显然 α1 和 α2,α1 和 α3,α2 和 α3 线性无关 (不在一条直线上), 但 α2=α1+α3, 所以向量组 {α1,α2,α3} 线性相关。
这个例题说明, 向量 α1、α2、α3 属于二维的平面向量空间, 而向量组的元素个数是 3, 超过了向量空间的维数 2 , 因而线性相关。一般的结论是, n 维向量空间里 n+1 个以上的向量必线性相关。
例 若 α1 和 α2 线性相关, β1 和 β2 也线性相关, 那么, α1+β1 和 α2+β2 也线性相关,这个说法是否正确?
解:这个说法也是错误的,也用二维空间的向量证明。如图 4-15 所示, 向量定义如下: α1=(2,1),α2=(−2,−1),β1=(−1,2),β2=(−2,4),则有 α1+β1=(1,3),α2+β2=(−4,3);α1+β1 和 α2+β2 不在一条直线上, 因而 α1+β1 和 α2+β2线性无关。
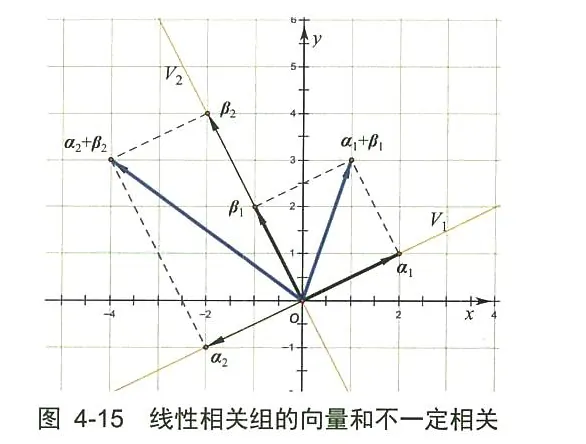
这个例题说明, α1 和 α2 在空间 V1 (直线) 上, β1 和 β2 在空间 V2 (直线) 上, 两个不同空间上的向量 (零向量除外) 相加, 必然会进入第三个空间(直线)、第四个空间(直线)……以致布满整个二维空间 (平面), 显然 α1+β1 和 α2+β2 绝大部分线性无关。
秩和维度的关系
理解向量组的秩和维数关系,例如 a1,a2 在 XOZ 平面上, b1,b2 在XOY 平面上,这2个平面组成了一个立方体,所以
a1,a2,b1,b2 组成的秩为3.
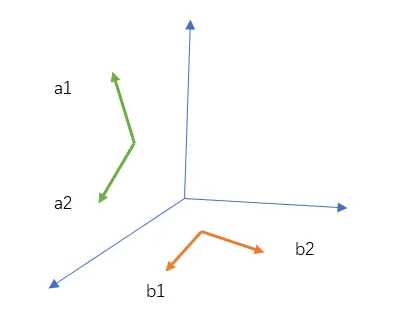
现在换成更具体的数字,在XOZ表示y坐标为0, 在XOY表示z坐标为0, 可以假设
a1=(1,0,2)
a2=(3,0,4)
b1=(1,2,0)
b1=(2,3,2)
此时他们向量组成的值就是3.
D=131200232400 极大线性无关组的求法
下面介绍一种利用初等行变换求向量组的极大无关组的方法。
例 求列向量组
α1=−1100,α2=−12−11,α3=0−11−1,α4=1−323,α5=2−641 的秩与一个极大无关组,并用该极大无关组线性表出向量组中的其余向量.
解 对矩阵 A=[α1α2α3α4α5] 作初等行变换化为阶梯形矩阵:
A=−1100−12−110−11−11−3232−641→−1000−11−100−1101−2252−445→−1000−11000−1001−2012−401→−1000−11000−1001−2102−410=B, 令
B=[β1β2β3β4β5]. 阶梯形矩阵 B 中有 3 行不为零,故秩 {α1,α2,α3,α4,α5}=3 ;又 B 的非零首元分别位于1、2、4列,则 β1,β2,β4 是 B 的一个列极大无关组,相应地, α1,α2,α4 是 α1 , α2,α3,α4,α5 的一个极大无关组。
进一步将 A 化为行最简形矩阵:
A→B→100001001−10000101−210=C=[γ1γ2γ3γ4γ5] 同理, γ1,γ2,γ4 是 C 的一个列极大无关组,且易知 γ3=γ1−γ2,γ5=γ1−2γ2+γ4 .相应地,有 α3=α1−α2,α5=α1−2α2+α4 。
思考:该向量组是否还有其他的极大无关组?
注:上面表达式的系数恰是矩阵列向量的值,具体原因在 向量组等价 有解释。
 {width=500px}
{width=500px}
 {width=500px}
{width=500px} {width=500px}
{width=500px}

