12._矩阵的秩的意义_向量版

说明 本文介绍矩阵的秩，是从向量空间角度进行理解，适合具有一定线性基础的人进行阅读，如果您是初学者，推荐你首先查看矩阵的秩的意义(方程组版) 的课程进行理解。矩阵的秩的本质反映的是方程组里，有效的方程的个数。

矩阵的秩的意义(向量版)

在线性代数中，一个矩阵的秩是其非零子式的最高阶数，一个向量组的秩则是其最大无关组所含的向量个数。

矩阵的秩是反映向量之间分布上的集中或限制程度的一个数值。它表示一组n维向量中最多有几个向量是无关的。如果一个矩阵满秩，说明这组向量中最多有n个向量是无关的，若加进来第n+1个向量，该组一定相关。矩阵的秩也可以反映矩阵的行或列中包含的独立方程式的个数。如果矩阵不满秩，那么矩阵会化简出有全零行，主元就“不完全”。

矩阵乘以一个向量就是把这个向量映射到列空间中去, 同时矩阵的秩也是其列空间的维数。 如果矩阵乘以一个图形 (向量的集合), 就会把这个图形统统变换到列空间去。变换后的图形维数最大不能超过列空间的维数。举几个例子: 对于二阶矩阵 $\boldsymbol{A}=\left[\begin{array}{cc}1 & 1.5 \\ 0 & 1\end{array}\right]$, 其行列式 $\operatorname{det}(\boldsymbol{A})=\left|\begin{array}{cc}1 & 1.5 \\ 0 & 1\end{array}\right|=-0.5 \neq 0$, 因此 $R(\boldsymbol{A})=2$; 对于二阶矩阵 $\boldsymbol{B}=\left[\begin{array}{cc}1 & 2 \\ 0.5 & 1\end{array}\right]$, 其行列式 $\operatorname{det}(\boldsymbol{B})=\left|\begin{array}{cc}1 & 2 \\ 0.5 & 1\end{array}\right|=0$, 故 $R(\boldsymbol{B})<2$, 进而得到 $R(\boldsymbol{B})=1$; 矩阵 $\boldsymbol{A}$ 和 $\boldsymbol{B}$ 对单位圆上向量的变化图形如图 5-31 所示。

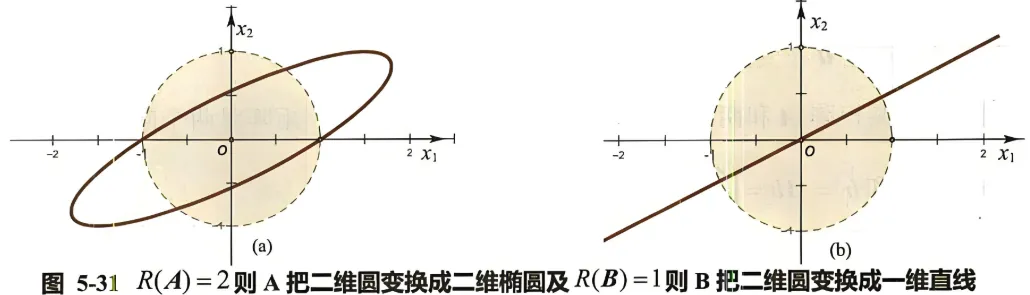
显然,

当二阶矩阵的秩等于 2 时, 矩阵把二维的圆形仍然变换为二维的椭圆图形; 当矩阵的秩降低为 1 时, 矩阵变换后的图形退化为一维的线段。

同样地, 三阶矩阵对于空间球面上的向量的变换图形是:

当矩阵的秩等于 3 时, 单位球被变换成三维空间中的一个椭圆球 (三维图形); 当矩阵的秩等于 2 时, 单位球被变换成三维空间中的一个椭圆面 (二维图形); 当矩阵的秩等于 1 时, 单位球被变换成三维空间中的一个线段 (一维图形)。

换句话说，矩阵的秩的大小，可以看成对图形降维的尺度。

矩阵的秩的定义

在 $m \times n$ 矩阵 $A$ 中，任取 $k$ 行与 $k$ 列 $(k \leq m, k \leq n)$ ，位于这些行列交叉处的 $k^2$ 个元 素，不改变它们在 $A$ 中所处的位置次序而得的 $k$ 阶行列式，称为矩阵 $A$ 的 $k$ 阶子式。 $m \times n$ 矩阵 $A$ 中的 $k$ 阶子式共有 $C_m^k \cdot C_n^k$ 个. 设在矩阵 $A$ 中有一个不等于 0 的 $r$ 阶子式 $D_1$ 且所有 $r+1$ 阶子式 (如果存在的话)全等于 0 ，那么 $D$ 称为矩阵 $A$ 的最高阶非零子式，数 $r$ 称为矩阵 $A$ 的秩，记作 $R(A)$

并规定：零矩阵的秩等于 0.

由行列式按行（列）展开的性质可知，若 $A$ 的所有 $r+1$ 阶子式全等于零，则所有高于 $r+1$ 阶的子式也全为 0 ，因此， $r$ 阶非零子式 $D$ 被称为最高阶非零子式， 而矩阵 $A$ 的秩 $R(\boldsymbol{A})$ 就是非零子式的最高阶数. 由此可得，若矩阵 $\boldsymbol{A}$ 中有某个 $k$ 阶子式不为 0 ，则 $R(\boldsymbol{A}) \geq k$ 若矩阵 $\boldsymbol{A}$ 中所有 $k$ 阶子式全为 0 ，则 $R(\boldsymbol{A})<k$. 对于 $n$ 阶矩阵 $A$ 因为 $A$ 的 $n$ 阶子式只有一个 $|\boldsymbol{A}|$ ， 所以，当 $|A| \neq 0$ 时， $R(A)=n$ ， 当 $|\boldsymbol{A}|=0$ 时， $R(\boldsymbol{A})<n$ 从而可逆矩阵的秩等于它的阶数，而不可逆矩阵的秩小于它 的阶数. 因此，可逆矩阵又称为满秩矩阵，不可逆矩阵又称为降秩矩阵.

例 求

\left|\begin{array}{ccc} 1 & 1 & 2 \ -1 & 2 & 0 \ 0 & 3 & 2 \end{array}\right|=0, \quad\left|\begin{array}{ccc} 1 & 1 & 3 \ -1 & 2 & 1 \ 0 & 3 & 4 \end{array}\right|=0, \quad\left|\begin{array}{ccc} 1 & 2 & 3 \ -1 & 0 & 1 \ 0 & 2 & 4 \end{array}\right|=0, \quad\left|\begin{array}{ccc} 1 & 2 & 3 \ 2 & 0 & 1 \ 3 & 2 & 4 \end{array}\right|=0

B =\left(\begin{array}{ccccc} 2 & -3 & 4 & 4 & 5 \ 0 & -2 & 1 & -1 & 3 \ 0 & 0 & 0 & 0 & 4 \ 0 & 0 & 0 & 0 & 0 \end{array}\right)

\left|\begin{array}{ccc} 2 & -3 & 5 \ 0 & -2 & 3 \ 0 & 0 & 4 \end{array}\right|=-16 \neq 0