16._正交矩阵

在学习本章时，必须跟进整体向量的思路。比如给你两个向量：$a,b$，我们先定义$a,b$的长度和夹角，如果他们不共线那就可以扩张为一个平面，既然能扩张为一个面，进而要研究如何找到一组正交基，然后给出施密特正交化，有了正交化后，再把模长单位化（即让模长为1），这样就可以到的新的空间坐标系，这个新的空间坐标系就是正交矩阵。换句话说，本掌内容是一环扣着一环，所以，在阅读本文前，建议已经了解前面介绍的内容。

下图展示了我们处理向量的基本过程：给你任意两个向量，我们先让他们正交，再让他们单位化，这就是前面所学的内容。示意图如下小黄脸从不开心到开心再到哈哈大笑。

作为初学者最大的疑问是：怎么又提出正交矩阵这个概念？这是因为一个矩阵乘以一个向量相当于一个线性变换，只有正交矩阵不改变向量根本属性。后面会学到二次型，比如一个圆当使用普通矩阵进行变换时，会变成椭圆（通常长度，角度都会改变），但只有正交变换会让圆仍然保持圆（长度、角度不变，或者把正交矩阵看成坐标轴旋转）

正交矩阵的数学定义及性质

如果 $n$ 阶矩阵 $A$ 满足 $A^{\mathrm{T}} A=E$ , 那么称 $A$ 为正交矩阵，简称正交阵.

设矩阵 $A$ 是 $n$ 阶方阵，则下列结论等价: (1) $A$ 是 $n$ 阶正交阵； (2) $A$ 的列向量组是 $\mathbf{R}^n$ 的一个规范正交基; (3) $A$ 的行向量组是 $\mathbf{R}^n$ 的一个规范正交基. 证明 (1) $\Leftrightarrow(2)$ ： 将矩阵 $A$ 按列分块 $A=\left(\alpha_1, \alpha_2, \cdots, \alpha_n\right)$ 如果 $A$ 是 $n$ 阶正交阵， 则公式 $A^T A=E$ 可表示为 $\left(\begin{array}{l}\alpha_1^T \\ \alpha_2^2 \\ \vdots \\ a_n^2\end{array}\right)\left(\alpha_1, \alpha_2, \cdots, \alpha_n\right)=\left(\begin{array}{cccc}1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & \cdots & 1\end{array}\right)$, 亦即 $\quad \boldsymbol{\alpha}_i^{\top} \boldsymbol{\alpha}_j=\delta_{i j}=\left\{\begin{array}{ll}1, & \text { 当 } i=j, \\ 0, & \text { 当 } i \neq j\end{array}(i, j=1,2, \cdots, n)\right.$, 这说明 $A$ 的列向量都是 $n$ 维单位向量，且两两正交，从而是 $\mathbf{R}^n$ 的一个规范正交基.

于是公式 $A A^T=E$ 可表示为

所以

即: $A$ 的行向量也都是 $n$ 维单位向量，且两两正交，从而是 $\mathbf{R}^n$ 的一个规范正交基.

克罗内克函数

现在跳脱线性代数，仅从高中函数的角度看$\boldsymbol{\delta}_{i j}$ ,当 $i=j$时，其值为1，当 当 $i \ne j$时，其值为0,

这个函数被称作克罗内克函数，他完美地同时概括了“标准”和“正交”两个条件

数学性质

1．正交矩阵的逆：$Q^T=Q^{-1}$ ，正交矩阵的转置 $=$ 正交矩阵的逆；

2．正交矩阵的行列式：行列式的取值只有两种可能（1）或（－1）； 这个证明比较简单，因为 $A^T A=E$, 两边取行列式得 $|A^TA|=|E|=>|A|=1 or |A|=-1$

3．向量正交：将 $Q$ 视作由若干行向量组成，则这些行向量两两相互正交；若将 $Q$ 视作由若干列向量组成，则这些列向量也两两相互正交；

4．保持长度不变：$Q \vec{x}=\vec{y}$ ，将 $Q$ 视作一个矩阵映射时，左乘一个向量 $x$ 后，得到的结果向量 $y$ 的长度与向量 $x$ 的长度相同，记作：$\|\vec{x}\|=\|\vec{y}\|$ ；

5．保持角度不变：如果有两个向量 $\overrightarrow{x_1}, \overrightarrow{x_2}$ ，它们的夹角是为 $(\theta)$ ，那么 $\overrightarrow{x_1}, \overrightarrow{x_2}$ 经过同一个正交矩阵映射后，得到的新向量 $Q \overrightarrow{x_1}, Q \overrightarrow{x_2}$ 之间的夹角仍然是 $(\theta)$ 。这意味着正交矩阵的映射不改变向量之间的夹角，只是对向量进行了旋转、投影、镜像等操作。

总之，在正交矩阵下，一个图像保持不变。

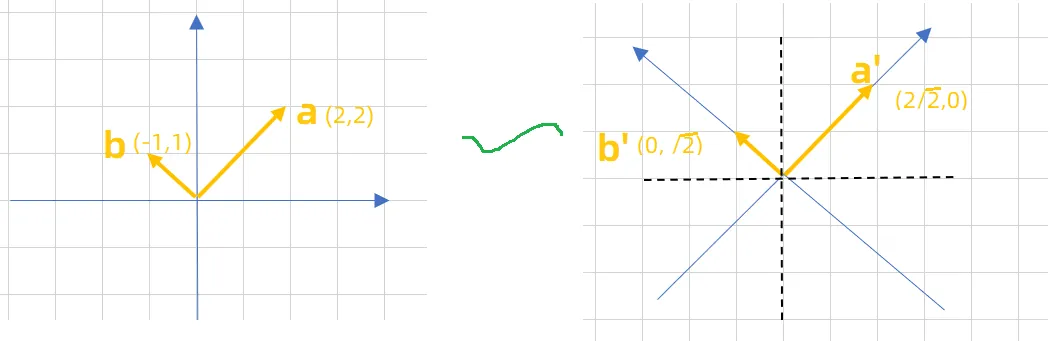
例假设存在一个矩阵 $A=\left[\begin{array}{cc}\frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\end{array}\right]$ ，试计算一个向量$a=(2,2)$ 和 $b=(-1,1)$在新基下的坐标值。

解：容易验证：他是方阵，他的模长为$\sqrt{\frac{\sqrt{2}}{2}^2 + (\frac{\sqrt{2}}{2})^2}=1$， 而且点积为零，所以矩阵$A$是一个正交矩阵。

此时我们要将自然基下的一个坐标 $x(2,2)$ 转换到 $A$ 这组基下。 依据坐标转换公式：$A^{-1}[x]_E=[x]_A$ 即可求得： 第一步：求 $A^{-1}$ ，用到的性质：正交矩阵的逆＝正交矩阵的转置

第二步：代入坐标转换公式

即：$[x]_a=\left[\begin{array}{c}2 \sqrt{2} \\ 0\end{array}\right]$

同理可的 $[x]_b=\left[\begin{array}{c}0 \\ \sqrt{2} \end{array}\right]$

下图显示了上面正交矩阵的作用。一个向量$a=(2,2)$ 和$b=(-1,1)$ 在矩阵A的作用下，变成了$a'=(2\sqrt{2},0)$ 和$b'=(0,\sqrt{2})$ ，神奇的事情发生了，你会发现 $a,b$的长度和$a,b$之间的夹角都没有变。 换句话说，正交变换不改变图形的性质

事实上，矩阵A如果写成下面形式，你就发现他本身就是一个 旋转矩阵

总之，对于正交矩阵，你可以理解为，在正交矩阵下图形会保持原有的长度和角度。 两个向量长度和夹角都保持不变。

为啥又搞出一个正交矩阵？

考虑下面两个矩阵：

$A^{T} A=E$ $A^{-1} A=E$

如果$A^{T} =A^{-1}$ 这个矩阵就算正交矩阵。单独看正交矩阵意义不大，但是如果放在图形变换里，那意义就太大了：

正交矩阵不改变图形的性质。

做一个简单的类别：

矩阵变换 类比 相似三角形 正交变换 类比 全等三角形

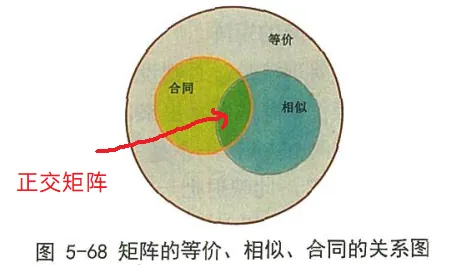
矩阵会有三大性质：等价、相似与合同。而正交矩阵是相似与合同的交集，因此具有最优秀的性质。

在前面介绍过，相似变换，相当于从不同的视角看图片，而正交变换可以看成从正面垂直角度看，具有最好的视角。

例验证矩阵 $P=\left(\begin{array}{cccc}\frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\end{array}\right)$ 是正交阵. 证明 容易验证 $P$ 的每个列向量都是单位向量，且两两正交，所以 $P$ 是正交阵。 正交矩阵具有如下性质: (i) 若 $A$ 为正交阵，则 $A ^{-1}= A ^{ T }$ 也是正交阵，且 $| A |=1$ 或 -1 ； (ii) 若 $A$ 和 $B$ 都是正交阵，则 $A B$ 也是正交阵.

正交变换的定义

若 $P$ 为正交矩阵，则线性变换 $y=P x$ 称为正交变换. 设 $y=P x$ 为正交变换，则有 $\| y \|=\sqrt{y^{ T } y }=\sqrt{ x ^{ T } P ^{ T } P x }=\sqrt{ x ^{ T } x }=\| x \|$. 因此正交变换保持向量的长度不变.

矩阵对称时的特征值分解

如果矩阵是对称的，那么矩阵的特征值分解实际上可以是一种非常简单但有用的形式。

对于一个 $n \times n$ 的实对称矩阵 $A$, 可以表示为:

其中:

• $Q$ 是一个正交矩阵, 其列向量是 $A$ 的单位正交特征向量。

• $\Lambda$ 是一个对角矩阵, 其对角线上的元素是 A 的特征值。

如果我们把（1）写成类似矩阵相似的形式

比较（1）（2），如果 $Q^T =Q^{-1}$ 就好了。这回引入后面介绍的合同。更详细介绍，参考附录2.

注意到我们上次所做的普通正方形矩阵特征分解的区别了吗？是的，现在具有特征向量的矩阵实际上是正交的, 因此矩阵的逆可以用转置来代替, 这比处理逆容易得多。

例已知矩阵 $A=\left(\begin{array}{ccc}0 & -1 & 1 \\ 2 & -3 & 0 \\ 0 & 0 & 0\end{array}\right)$ 求 $A^{99}$ ；

解：(1) 通过解方程可得特征值，即有

由此可得各特征值对应的特征向量为为

把三个特征向量构成的矩阵记作

从而有

于是由求矩阵幂的特征值法，可得

容易求得矩阵 $\boldsymbol{P}$ 的逆矩阵为

把 $P$ 和 $P^{-1}$ 代入式子 $\left(^*\right)$ ，从而有

这题来自2016年全国硕士研究生招生统一考试数学试题及详细参考解答(数三)，通过这道题感受《线性代数》的魅力，比如$A^{99}$次幂，如果死算，在人工时代，基本上是不可能的任务，但是利用特征值、特征向量，基础解析、相似、合同等概念，竟然把一个矩阵需要乘以99次转换为了对矩阵元素的运算。

从上面例子会得出后面二次型介绍的 实对称矩阵的对角化

例 设 3 阶矩阵 $A$ 的 3 个特征值分别为 $\lambda_1=1, \lambda_2=2$ ， $\lambda_3=3$ ，它们对应的特征向量分别为

求：（1）矩阵 $A$ （2）$A^T$ 的特征值与特征向量。

解（1）由于 3 阶矩阵 $A$ 有 3 个不同的特征值，因此 $A$ 可对角化．令 $P=\left(\alpha_1, \alpha_2, \alpha_3\right)$ ，由 $P=\left[\begin{array}{lll}1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 3 & 6\end{array}\right]$ ，可求得 $P^{-1}=\left[\begin{array}{rrr}3 & -3 & 1 \\ -3 & 5 & -2 \\ 1 & -2 & 1\end{array}\right]$ ，则由

可知，

（2）由于 $A$ 与 $A^T$ 有完全相同的特征值，因此 $A^T$ 的特征值为 $\lambda_1=1, \lambda_2=2, \lambda_3=3$ ．

由 $P^{-1} A P=\Lambda$ 可知，$P^T A^T\left(P^{-1}\right)^T=\Lambda$ ．

其中

因此，与 $A^T$ 的特征值 $\lambda_1=1, \lambda_2=2, \lambda_3=3$ 对应的特征向量分别为

其中 $c_1, c_2, c_3$ 均为非零常数． 本题在求解 $A^T$ 的特征向量时，从另一角度利用了 $P^{-1} A P=\Lambda$ 这一关系，读者应仔细体会．