1.3 基于Transformer的语言模型

Transformer 是一类基于注意力机制（Attention）的模块化构建的神经网络结构。给定一个序列，Transformer 将一定数量的历史状态和当前状态同时输入，然后进行加权相加。对历史状态和当前状态进行“通盘考虑”，然后对未来状态进行预测。基于 Transformer 的语言模型，以词序列作为输入，基于一定长度的上文和当前词来预测下一个词出现的概率。本节将先对 Transformer 的基本原理进行介绍，然后讲解如何利用 Transformer 构建语言模型。

1.3.1 Transformer

Transformer是由两种模块组合构建的模块化网络结构。两种模块分别为：（1）注意力（Attention）模块；（2）全连接前馈（Fully-connected Feedforward）模块。其中，自注意力模块由自注意力层（Self-Attention Layer）、残差连接（Residual Connections）和层正则化（Layer Normalization）组成。全连接前馈模块由全连接前馈层，残差连接和层正则化组成。两个模块的结构示意图如图1.5所示。以下详细介绍每个层的原理及作用。

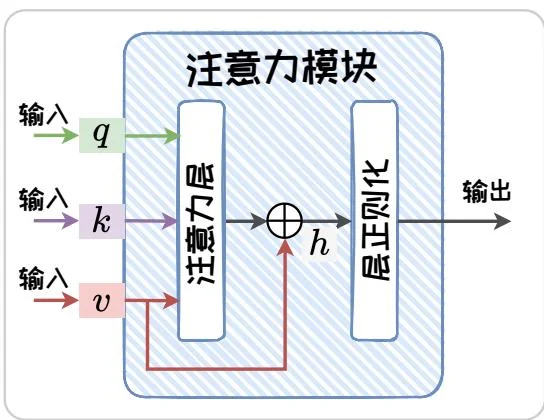
图1.5: 注意力模块与全连接前馈模块。

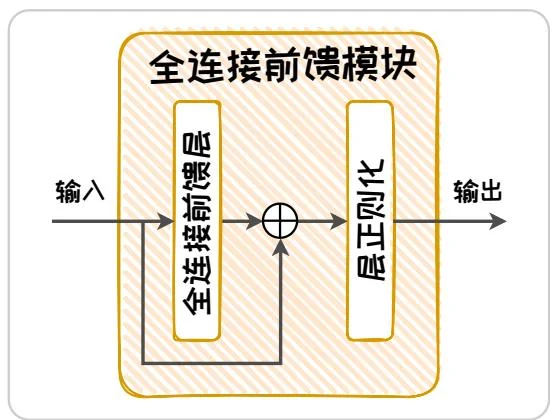
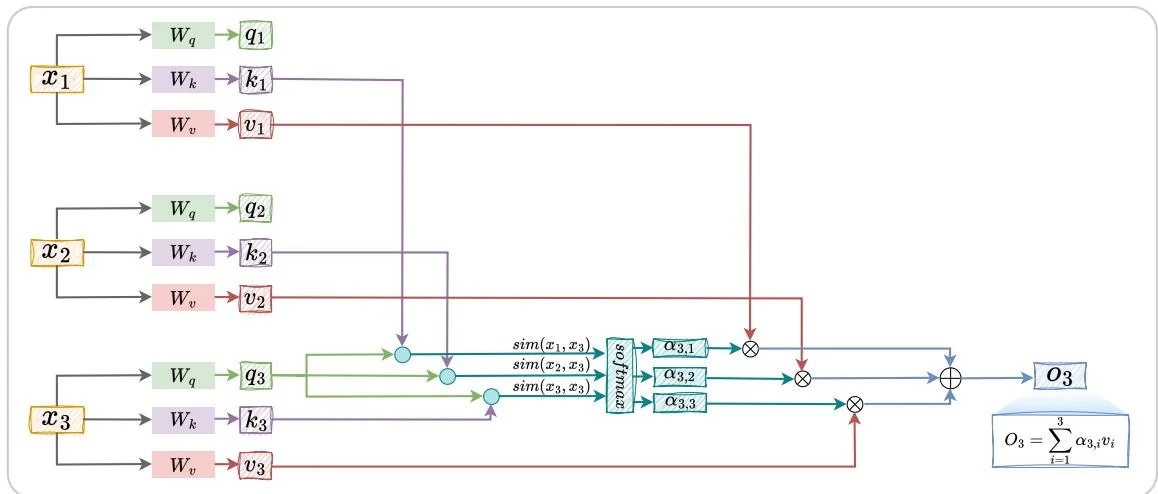
图1.6: 注意力机制示意图。

1. 注意力层（Attention Layer）

注意力层采用加权平均的思想将前文信息叠加到当前状态上。Transformer的注意力层将输入编码为 query，key，value 三部分，即将输入 $\{x_{1}, x_{2}, \ldots, x_{t}\}$ 编码为 $\{(q_{1}, k_{1}, v_{1}), (q_{2}, k_{2}, v_{2}), \ldots, (q_{t}, k_{t}, v_{t})\}$ 。其中，query 和 key 用于计算自注意力的权重 $\alpha$ ，value 是对输入的编码。具体的，

\operatorname {A t t e n t i o n} \left(x _ {t}\right) = \sum_ {i = 1} ^ {t} \alpha_ {t, i} v _ {i} 。 \tag {1.31}

其中，

\alpha_ {t, i} = \operatorname {s o f t m a x} \left(\operatorname {s i m} \left(x _ {t}, x _ {i}\right)\right) = \frac {\operatorname {s i m} \left(q _ {t} , k _ {i}\right)}{\sum_ {i = 1} ^ {t} \operatorname {s i m} \left(q _ {t} , k _ {i}\right)} 。 \tag {1.32}

其中， $sim(\cdot, \cdot)$ 用于度量两个输入之间的相关程度，softmax函数用于对此相关程度进行归一化。此外，

q _ {i} = W _ {q} x _ {i}, k _ {i} = W _ {k} x _ {i}, v _ {i} = W _ {v} x _ {i}, \tag {1.33}

其中， $W_{q}, W_{k}, W_{v}$ 分别为 query，key，value 编码器的参数。以包含三个元素的输入 $\{x_{1}, x_{2}, x_{3}\}$ 为例，Transformer 自注意力的实现图1.6所示。

2. 全连接前馈层 (Fully-connected Feedforward Layer)

全连接前馈层占据了Transformer近三分之二的参数，掌管着Transformer模型的记忆。其可以看作是一种Key-Value模式的记忆存储管理模块[7]。全连接前馈层包含两层，两层之间由ReLU作为激活函数。设全连接前馈层的输入为 $v$ ，全连接前馈层可由下式表示：

F F N (v) = \max \left(0, W _ {1} v + b _ {1}\right) W _ {2} + b _ {2} 。 \tag {1.34}

其中， $W_{1}$ 和 $W_{2}$ 分别为第一层和第二层的权重参数， $b_{1}$ 和 $b_{2}$ 分别为第一层和第二层的偏置参数。其中第一层的可看作神经记忆中的 key，而第二层可看作 value。

3. 层正则化 (Layer Normalization)

层正则化用以加速神经网络训练过程并取得更好的泛化性能 [1]。设输入到层正则化层的向量为 $v = \{v_{i}\}_{i=1}^{n}$ 。层正则化层将在 $v$ 的每一维度 $v_{i}$ 上都进行层正则化操作。具体地，层正则化操作可以表示为下列公式：

L N \left(v _ {i}\right) = \frac {\alpha \left(v _ {i} - \mu\right)}{\delta} + \beta 。 \tag {1.35}

其中， $\alpha$ 和 $\beta$ 为可学习参数。 $\mu$ 和 $\delta$ 分别是隐藏状态的均值和方差，可由下列公式分别计算。

\mu = \frac {1}{n} \sum_ {i = 1} ^ {n} v _ {i}, \quad \delta = \sqrt {\frac {1}{n} \sum_ {i = 1} ^ {n} \left(v _ {i} - \mu\right) ^ {2}} 。 \tag {1.36}

4. 残差连接 (Residual Connections)

引入残差连接可以有效解决梯度消失问题。在基本的Transformer编码模块中包含两个残差连接。第一个残差连接是将自注意力层的输入由一条旁路叠加到自注意力层的输出上，然后输入给层正则化。第二个残差连接是将全连接前馈层的输入由一条旁路引到全连接前馈层的输出上，然后输入给层正则化。

上述将层正则化置于残差连接之后的网络结构被称为Post-LN Transformer。与之相对的，还有一种将层正则化置于残差连接之前的网络结构，称之为Pre-LN

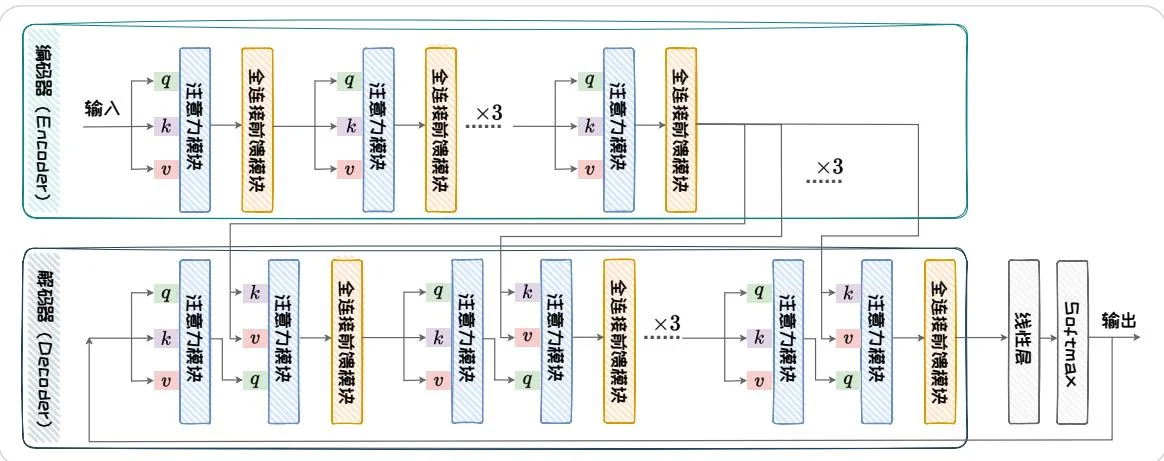
图1.7: Transfomer结构示意图。

Transformers。对比两者, Post-LN Transformer 应对表征坍塌 (Representation Collapse) 的能力更强, 但处理梯度消失略弱。而 Pre-LN Transformers 可以更好的应对梯度消失, 但处理表征坍塌的能力略弱。具体分析可参考文献 [7, 22]。

原始的Transformer采用Encoder-Decoder架构，其包含Encoder和Decoder两部分。这两部分都是由自注意力模块和全连接前馈模块重复连接构建而成。其整体结构如图1.7所示。其中，Encoder部分由六个级联的encoder layer组成，每个encoder layer包含一个注意力模块和一个全连接前馈模块。其中的注意力模块为自注意力模块（query，key，value的输入是相同的）。Decoder部分由六个级联的decoder layer组成，每个decoder layer包含两个注意力模块和一个全连接前馈模块。其中，第一个注意力模块为自注意力模块，第二个注意力模块为交叉注意力模块(query，key，value的输入不同)。Decoder中第一个decoder layer的自注意力模块的输入为模型的输出。其后的decoder layer的自注意力模块的输入为上一个decoderlayer的输出。Decoder交叉注意力模块的输入分别是自注意力模块的输出(query)和最后一个encoder layer的输出（key，value）。

Transformer的Encoder部分和Decoder部分都可以单独用于构造语言模型，分别对应Encoder-Only模型和Decoder-Only模型。Encoder-Only模型和Decoder-Only模型的具体结构将在第二章中进行详细介绍。

1.3.2 基于Transformer的语言模型

在Transformer的基础上，可以设计多种预训练任务来训练语言模型。例如，我们可以基于Transformer的Encoder部分，结合“掩词补全”等任务来训练Encoder-Only语言模型，如BERT[5]；我们可以同时应用Transformer的Endcoder和Decoder部分，结合“截断补全”、“顺序恢复”等多个有监督和自监督任务来训练Encoder-Decoder语言模型，如T5[18]；我们可以同时应用Transformer的Decoder部分，利用“下一词预测”任务来训练Decoder-Only语言模型，如GPT-3[3]。这些语言模型将在第二章中进行详细介绍。下面将以下一词预测任务为例，简单介绍训练Transformer语言模型的流程。

对词序列 $\{w_{1}, w_{2}, w_{3}, \ldots, w_{N}\}$ , 基于Transformer的语言模型根据 $\{w_{1}, w_{2}, \ldots, w_{i}\}$ 预测下一个词 $w_{i+1}$ 出现的概率。在基于Transformer的语言模型中, 输出为一个向量, 其中每一维代表着词典中对应词的概率。设词典 $D$ 中共有 $|D|$ 个词 $\{\hat{w}_{1}, \hat{w}_{2}, \ldots, \hat{w}_{|D|}\}$ 。基于Transformer的语言模型的输出可表示为 $o_{i} = \{o_{i}[\hat{w}_{d}]\}_{d=1}^{D}$ , 其中, $o_{i}[\hat{w}_{d}]$ 表示词典中的词 $\hat{w}_{d}$ 出现的概率。因此, 对Transformer的语言模型对词序列 $\{w_{1}, w_{2}, w_{3}, \ldots, w_{N}\}$ 整体出现的概率的预测为:

P \left(w _ {1: N}\right) = \prod_ {i = 1} ^ {N - 1} P \left(w _ {i + 1} \mid w _ {1: i}\right) = \prod_ {i = 1} ^ {N} o _ {i} \left[ w _ {i + 1} \right] \tag {1.37}

与训练 RNN 语言模型相同，Transformer 语言模型也常用如下交叉熵函数作为损失函数。

l _ {C E} \left(o _ {i}\right) = - \sum_ {d = 1} ^ {| D |} I \left(\hat {w} _ {d} = w _ {i + 1}\right) \log o _ {i} \left[ w _ {i + 1} \right] = - \log o _ {i} \left[ w _ {i + 1} \right] 。 \tag {1.38}

其中， $I(\cdot)$ 为指示函数，当 $\hat{w}_d = w_{i + 1}$ 时等于1，当 $\hat{w}_d\neq w_{i + 1}$ 时等于0。

设训练集为 S，Transformer 语言模型的损失可以构造为：

L (S, W) = \frac {1}{N | S |} \sum_ {s = 1} ^ {| S |} \sum_ {i = 1} ^ {N} l _ {C E} \left(o _ {i, s}\right) \tag {1.39}

其中， $o_{i,s}$ 为Transformer语言模型输入样本s的前 $i$ 个词时的输出。在此损失的基础上，构建计算图，进行反向传播，便可对Transformer语言模型进行训练。

上述训练过程结束之后，我们可以将Encoder的输出作为特征，然后应用这些特征解决下游任务。此外，还可在“自回归”的范式下完成文本生成任务。在自回归中，第一轮，我们首先将第一个词输入给Transformer语言模型，经过解码，得到一个输出词。然后，我们将第一轮输出的词与第一轮输入的词拼接，作为第二轮的输入，然后解码得到第二轮的输出。接着，将第二轮的输出和输入拼接，作为第三轮的输入，以此类推。每次将本轮预测到的词拼接到本轮的输入上，输入给语言模型，完成下一轮预测。在循环迭代的“自回归”过程中，我们不断生成新的词，这些词便构成了一段文本。与训练RNN语言模型一样，Transformer模型的预训练过程依然采用第1.2.2节中提到的“Teacher Forcing”的范式。

相较于 RNN 模型串行的循环迭代模式，Transformer 并行输入的特性，使其容易进行并行计算。但是，Transformer 并行输入的范式也导致网络模型的规模随输入序列长度的增长而平方次增长。这为应用 Transformer 处理长序列带来挑战。