1.4 语言模型的采样方法

语言模型的输出为一个向量，该向量的每一维代表着词典中对应词的概率。在采用自回归范式的文本生成任务中，语言模型将依次生成一组向量并将其解码为文本。将这组向量解码为文本的过程成为语言模型解码。解码过程显著影响着生成文本的质量。当前，两类主流的解码方法可以总结为(1).概率最大化方法;(2).随机采样方法。两类方法分别在下面章节中进行介绍。

1.4.1 概率最大化方法

设词典为 $D$ ，输入文本为 $\{w_{1},w_{2},w_{3},\dots,w_{N}\}$ ，第 $i$ 轮自回归中输出的向量为 $o_i = \{o_i[w_d]\}_{d = 1}^{|D|}$ ，模型在 $M$ 轮自回归后生成的文本为 $\{w_{N + 1},w_{N + 2},w_{N + 3},\ldots ,w_{N + M}\}$ 。生成文档的出现的概率可由下式进行计算。

P \left(w _ {N + 1: N + M}\right) = \prod_ {i = N} ^ {N + M - 1} P \left(w _ {i + 1} \mid w _ {1: i}\right) = \prod_ {i = N} ^ {N + M - 1} o _ {i} \left[ w _ {i + 1} \right] \tag {1.40}

基于概率最大化的解码方法旨在最大化 $P(w_{N + 1:N + M})$ ，以生成出可能性最高的文本。该问题的搜索空间大小为 $M^D$ ，是NP-Hard问题。现有概率最大化方法通常采用启发式搜索方法。本节将介绍两种常用的基于概率最大化的解码方法。

1.贪心搜索（Greedy Search）

贪心搜索在在每轮预测中都选择概率最大的词，即

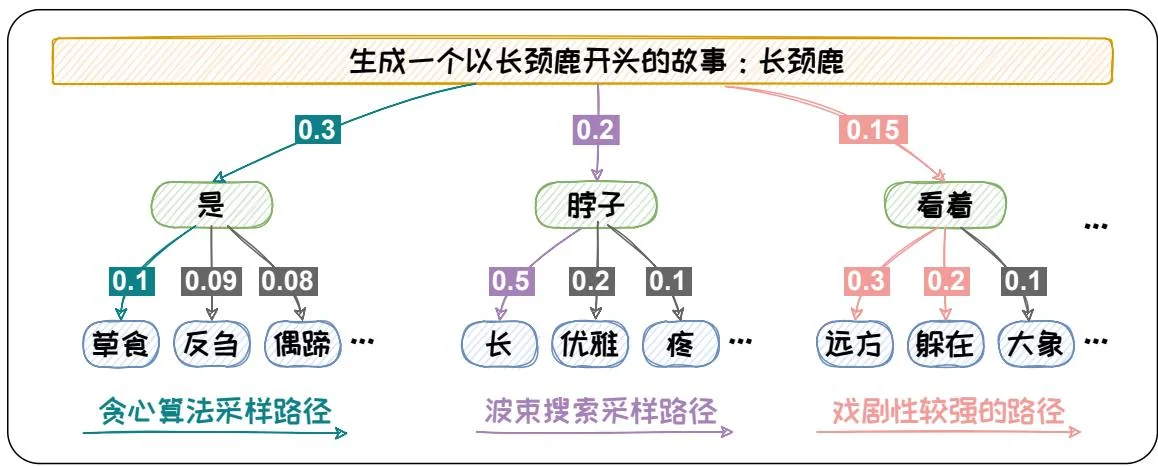
w _ {i + 1} = \arg \max _ {w \in D} o _ {i} [ w ] \tag {1.41}

贪心搜索只顾“眼前利益”，忽略了“远期效益”。当前概率大的词有可能导致后续的词概率都很小。贪心搜索容易陷入局部最优，难以达到全局最优解。以图1.8为例，当输入为“生成一个以长颈鹿开头的故事：长颈鹿”时，预测第一个词为“是”的概率最高，为0.3。但选定“是”之后，其他的词的概率都偏低。如果按照贪心搜索的方式，我们最终得到的输出为“是草食”。其概率仅为0.03。而如果我们在第一个词选择了概率第二的“脖子”，然后第二个词选到了“长”，最终的概率可以达到0.1。通过此例，可以看出贪心搜索在求解概率最大的时候容易陷入局部最优。为缓解此问题，可以采用波束搜索（Beam Search）方法进行解码。

2. 波束搜索 (Beam Search)

波束搜索在每轮预测中都先保留 $b$ 个可能性最高的词 $B_{i} = \{w_{i + 1}^{1},w_{i + 1}^{2},\dots,w_{i + 1}^{b}\}$ 即：

\min \left\{o _ {i} [ w ] f o r w \in B _ {i} \right\} > \max \left\{o _ {i} [ w ] f o r w \in D - B _ {i} \right\}. \tag {1.42}

图1.8：贪心搜索与波束搜索对比以及概率最大化解码的潜在问题。

在结束搜索时，得到 $M$ 个集合，即 $\{B_i\}_{i=1}^M$ 。找出最优组合使得联合概率最大，即：

\left\{w _ {N + 1}, \dots , w _ {N + M} \right\} = \arg \max _ {\left\{w ^ {i} \in B _ {i} \text {f o r} 1 \leq i \leq M \right\}} \prod_ {i = 1} ^ {M} o _ {N + i} \left[ w ^ {i} \right] 。 \tag {1.43}

继续以上面的“生成一个以长颈鹿开头的故事”为例，从图1.8中可以看出如果我们采用 $b = 2$ 的波束搜索方法，我们可以得到“是草食”，“是反刍”，“脖子长”，“脖子优雅”四个候选组合，对应的概率分别为：0.03，0.027，0.1，0.04。我们容易选择到概率最高的“脖子长”。

但是，概率最大的文本通常是最为常见的文本。这些文本会略显平庸。在开放式文本生成中，无论是贪心搜索还是波束搜索都容易生成一些“废话文学”一重复且平庸的文本。其所生成的文本缺乏多样性[19]。如在图1.8中的例子所示，概率最大的方法会生成“脖子长”。“长颈鹿脖子长”这样的文本新颖性较低。为了提升生成文本的新颖度，我们可以在解码过程中加入一些随机元素。这样的话就可以解码到一些不常见的组合，从而使得生成的文本更具创意，更适合开放式文本任务。在解码过程中加入随机性的方法，成为随机采样方法。下节将对随机采样方法进行介绍。

1.4.2 随机采样方法

为了增加生成文本的多样性，随机采样的方法在预测时增加了随机性。在每轮预测时，其先选出一组可能性高的候选词，然后按照其概率分布进行随机采样，采样出的词作为本轮的预测结果。当前，主流的Top-K采样和Top-P采样方法分别通过指定候选词数量和划定候选词概率阈值的方法对候选词进行选择。在采样方法中加入Temperature机制可以对候选词的概率分布进行调整。接下来将对Top-K采样、Top-P采样和Temperature机制分别展开介绍。

1. Top-K 采样

Top-K采样在每轮预测中都选取 $K$ 个概率最高的词 $\{w_{i + 1}^{1},w_{i + 1}^{2},\dots,w_{i + 1}^{K}\}$ 作为本轮的候选词集合，然后对这些词的概率用softmax函数进行归一化，得到如下分布函数

p \left(w _ {i + 1} ^ {1}, \dots , w _ {i + 1} ^ {K}\right) = \left\{\frac {\exp \left(o _ {i} \left[ w _ {i + 1} ^ {1} \right]\right)}{\sum_ {j = 1} ^ {K} \exp \left(o _ {i} \left[ w _ {i + 1} ^ {j} \right]\right)}, \dots , \frac {\exp \left(o _ {i} \left[ w _ {i + 1} ^ {K} \right]\right)}{\sum_ {j = 1} ^ {K} \exp \left(o _ {i} \left[ w _ {i + 1} ^ {j} \right]\right)} \right\}. \tag {1.44}

然后根据该分布采样出本轮的预测的结果，即

w _ {i + 1} \sim p \left(w _ {i + 1} ^ {1}, \dots , w _ {i + 1} ^ {K}\right) 。 \tag {1.45}

Top-K采样可以有效的增加生成文本的新颖度，例如在上述图1.8所示的例子中选用Top-3采样的策略，则有可能会选择到“看着躲在”。“长颈鹿看着躲在”可能是一个极具戏剧性的悬疑故事的开头。

但是，将候选集设置为固定的大小 $K$ 将导致上述分布在不同轮次的预测中存在很大差异。当候选词的分布的方差较大的时候，可能会导致本轮预测选到概率较小、不符合常理的词，从而产生“胡言乱语”。例如，在如图1.9(a)所示的例子中，Top-2采样有可能采样出“长颈鹿有四条裤子”。而当候选词的分布的方差较小的时候，甚至趋于均匀分布时，固定尺寸的候选集中无法容纳更多的具有相近概率的词，导致候选集不够丰富，从而导致所选词缺乏新颖性而产生“枯燥无趣”的

（a）Top-k胡言乱语

（b）Top-k枯燥无味
图1.9: Top-K采样的潜在问题及其与Top-P方法的对比。

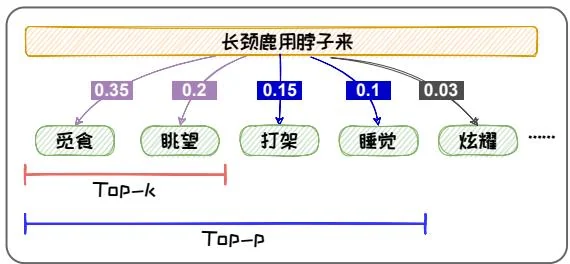
文本。例如，在如下图1.9(b)所示的例子中，通过Top-2采样，我们只能得到“长颈鹿用脖子来觅食”或者“长颈鹿用脖子来眺望”，这些都是人们熟知的长颈鹿脖子的用途，缺乏新意。但是其实长颈鹿的脖子还可以用于打架或睡觉，Top-2采样的方式容易将这些新颖的不常见的知识排除。为了解决上述问题，我们可以使用Top-P采样，也称Nucleus采样。

2. Top-P 采样

为了解决固定候选集所带来的问题，Top-P采样（即Nucleus采样）被提出[9]。其设定阈值p来对候选集进行选取。其候选集可表示为 $S_{p} = \{w_{i + 1}^{1},w_{i + 1}^{2},\dots,w_{i + 1}^{|S_{p}|}\}$ 其中，对 $S_{p}$ 有， $\sum_{w\in S_p}o_i[w]\geq p$ 。候选集中元素的分布服从

p \left(w _ {i + 1} ^ {1}, \dots , w _ {i + 1} ^ {\left| S _ {p} \right|}\right) = \left\{\frac {\exp \left(o _ {i} \left[ w _ {i + 1} ^ {1} \right]\right)}{\sum_ {j = 1} ^ {\left| S _ {p} \right|} \exp \left(o _ {i} \left[ w _ {i + 1} ^ {j} \right]\right)}, \dots , \frac {\exp \left(o _ {i} \left[ w _ {i + 1} ^ {\left| S _ {p} \right|} \right]\right)}{\sum_ {j = 1} ^ {\left| S _ {p} \right|} \exp \left(o _ {i} \left[ w _ {i + 1} ^ {j} \right]\right)} \right\}. \tag {1.46}

然后根据该分布采样出本轮的预测的结果，即

w _ {i + 1} \sim p \left(w _ {i + 1} ^ {1}, \dots , w _ {i + 1} ^ {\left| S _ {p} \right|}\right) 。 \tag {1.47}

应用阈值作为候选集选取的标准之后，Top-P采样可以避免选到概率较小、不符合常理的词，从而减少“胡言乱语”。例如在图1.9(a)所示例子中，我们若以0.9作为阈值，则就可以很好的避免“长颈鹿有四条裤子”的问题。并且，其还可以容

纳更多的具有相近概率的词，增加文本的丰富度，改善“枯燥无趣”。例如在图1.9(b)所示的例子中，我们若以0.9作为阈值，则就可以包含打架、睡觉等长颈鹿脖子鲜为人知的用途。

3. Temperature 机制

Top-K采样和Top-P采样的随机性由语言模型输出的概率决定，不可自由调整。但在不同场景中，我们对于随机性的要求可能不一样。比如在开放文本生成中，我们更倾向于生成更具创造力的文本，所以我们需要采样具有更强的随机性。而在代码生成中，我们希望生成的代码更为保守，所以我们需要较弱的随机性。引入Temperature机制可以对解码随机性进行调节。Temperature机制通过对Softmax函数中的自变量进行尺度变换，然后利用Softmax函数的非线性实现对分布的控制。设Temperature尺度变换的变量为 $T$ 。

引入 Temperature 后，Top-K 采样的候选集的分布如下所示：

p \left(w _ {i + 1} ^ {1}, \dots , w _ {i + 1} ^ {K}\right) = \left\{\frac {\exp \left(\frac {o _ {i} \left[ w _ {i + 1} ^ {1} \right]}{T}\right)}{\sum_ {j = 1} ^ {K} \exp \left(\frac {o _ {i} \left[ w _ {i + 1} ^ {j} \right]}{T}\right)}, \dots , \frac {\exp \left(\frac {o _ {i} \left[ w _ {i + 1} ^ {K} \right]}{T}\right)}{\sum_ {j = 1} ^ {K} \exp \left(\frac {o _ {i} \left[ w _ {i + 1} ^ {j} \right]}{T}\right)} \right\}. \tag {1.48}

引入Temperature后，Top-P采样的候选集的分布如下所示：

p (w _ {i + 1} ^ {1}, \dots ., w _ {i + 1} ^ {| S _ {p} |}) = \left\{\frac {e x p (\frac {o _ {i} [ w _ {i + 1} ^ {1} ]}{T})}{\sum_ {j = 1} ^ {| S _ {p} |} e x p (\frac {o _ {i} [ w _ {i + 1} ^ {j} ]}{T})}, \dots ., \frac {e x p (\frac {o _ {i} [ w _ {i + 1} ^ {| S _ {p} |} ]}{T})}{\sum_ {j = 1} ^ {| S _ {p} |} e x p (\frac {o _ {i} [ w _ {i + 1} ^ {j} ]}{T})} \right\}. \tag {1.49}

容易看出，当 $T > 1$ 时，Temperature机制会使得候选集中的词的概率差距减小，分布变得更平坦，从而增加随机性。当 $0 < T < 1$ 时，Temperature机制会使得候选集中的元素的概率差距加大，强者越强，弱者越弱，概率高的候选词会容易被选到，从而随机性变弱。Temperature机制可以有效的对随机性进行调节来满足不同的需求。

1.4_语言模型的采样方法