3._抽样 - Probability Theory and Mathematical Statistics

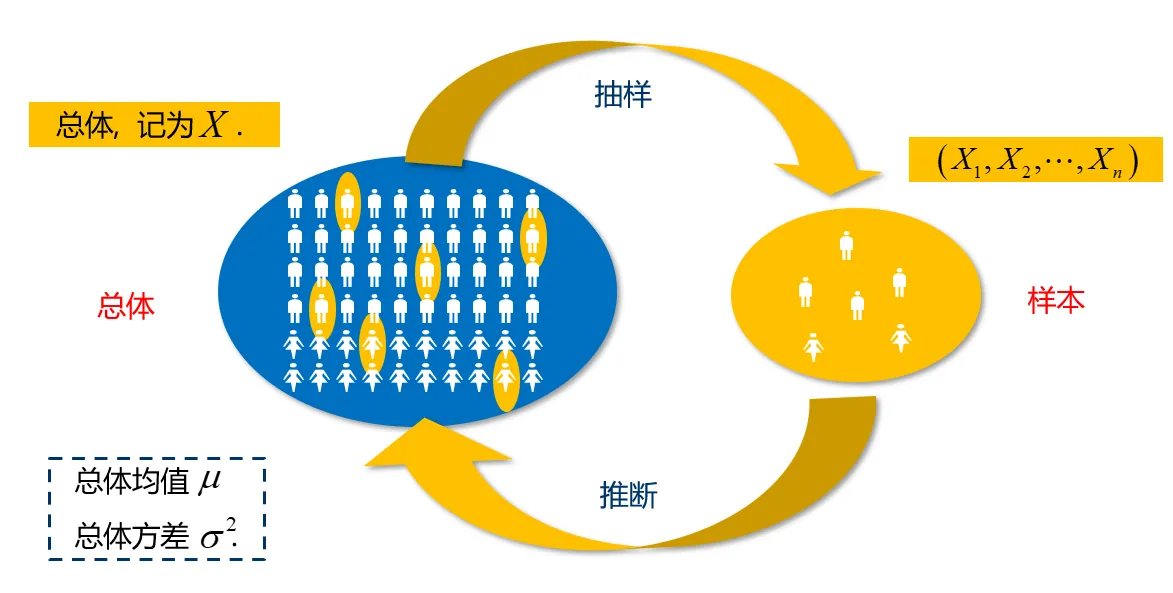
抽样

从总体中抽取样本的方法有很多，我们主要采用简单随机抽样的方法，即有放回地重复独立抽取，这样得到的样本称为简单随机样本 (简称样本). 记作 $\left(X_1, X_2, \cdots, X_n\right)$ . 在试验前，样本的观测值是不确定的，为了体现随机性，在数理统计中样本记作 $\left(X_1, X_2, \cdots, X_n\right)$ ，事实上是一个 $n$ 维随机向量. 通过实验或观测得到的数值称为样本观测值，记作 $\left(x_1, x_2, \cdots, x_n\right)$ ，其中 $n$ 称为样本容量(样本大小). 也就是说样本是一组随机变量，而样本观测值是抽样完成以后所得到的这组随机变量的一次具体取值. $图片$ {width=500px}

简单随机样本具有两个特点: (1) 独立性: $X_1, X_2, \cdots, X_n$ 是相互独立的; (2) 代表性: 每个个体 $X_i$ 的分布都和总体分布相同. 即 $X_i \sim f\left(x_i, \theta\right), i=1,2, \cdots, n$ .

① 设 $X$ 为离散型随机变量，则 $X \sim f(x ; \theta) \hat{=} P(X=x)$ 而样本 $\left(X_1, X_2, \cdots, X_n\right)$ 的联合分布律为:

\begin{aligned} f\left(x_1, x_2, \cdots, x_n ; \theta\right) & \hat{=} P\left(X_1=x_1, X_2=x_2, \cdots, X_n=x_n ; \theta\right) \\ & =P\left(X_1=x_1\right) P\left(X_2=x_2\right) \cdots P\left(X_n=x_n\right)=\prod_{i=1}^n P\left(X_i=x_i ; \theta\right) \end{aligned}

例某饮料厂生产的一种瓶装饮料规定净含量为 650 克．事实上不可能使得所有的饮料净含量均为 650 克．现从该厂生产的饮料中随机抽取 12 瓶测定其净含量，获得如下结果： $645,652,642,646,647,643,648,649,651,649,647,646$ ．这是一个容量为 12的样本观测值，对应的总体为该厂生产的瓶装饮料的净含量．

简单随机样本是一种非常理想化的样本，在实际应用中要获得严格意义下的简单随机样本并不容易．无特别声明，本书抽得的样本皆指简单随机样本．样本 $X_1, X_2, \cdots, X_n$ 可以视为相互独立的具有同一分布的随机变量，又称为独立同分布样本（即为 iid 样本），其联合分布即为总体分布。

若总体 $X$ 的分布函数为 $F(x), X_1, X_2, \cdots, X_n$ 为总体 $X$ 的一个样本，则 $X_1, X_2, \cdots, X_n$ 的联合分布函数为

F\left(x_1, x_2, \cdots, x_n\right)=\prod_{i=1}^n F\left(x_i\right) .

当总体 $X$ 为连续型随机变量时，若其概率密度为 $f(x)$ ，则样本的联合概率密度为

f\left(x_1, x_2, \cdots, x_n\right)=\prod_{i=1}^n f\left(x_i\right)

当总体 $X$ 为离散型随机变量时，若其概率分布为 $p(x)=P\{X=x\}$ ，则样本的联合概率分布为

p\left(x_1, x_2, \cdots, x_n\right)=p\left\{X=x_1, X=x_2, \cdots, X=x_n\right\}=\prod_{i=1}^n p\left(x_i\right) .

例 考察某厂的产品质量，将其产品分为合格品和不合格品，并以 0 表示合格品，以 1 表示不合格品，显然 $X \sim B(1, p), 0<p<1$ ．设 $X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的样本，求该样本的概率分布。

解总体 $X$ 的分布律为 $P\{X=i\}=p^i(1-p)^{1-i}, i=0,1$ ．因为样本 $X_1, X_2, \cdots, X_n$ 相互独立，且与总体 $X$ 同分布，所以样本的概率分布为

\begin{aligned} P\left\{X_1\right. & \left.=x_1, X_2=x_2, \cdots, X_n=x_n\right\} \\ & =P\left\{X_1=x_1\right\} \cdot P\left\{X_2=x_2\right\} \cdots P\left\{X_n=x_n\right\} \\ & =\prod_{i=1}^n p^{x_i}(1-p)^{1-x_i} \\ & =p^{\sum_{i=1}^n x_i}(1-p)^{n-\sum_{i=1}^n x_i}, x_i \in\{0,1\}, \quad i=1,2, \cdots, n . \end{aligned}

例设总体 $X \sim P(\lambda), ~\left(X_1, X_2, \cdots, X_6\right)$ 为取自该总体的一个样本，求样本 $\left(X_1, X_2, \cdots, X_6\right)$ 的联合分布律 $f\left(x_1, x_2, \cdots, x_6 ; \lambda\right)$ ？

解

f\left(x_1, x_2, \cdots, x_6 ; \lambda\right)=e^{-\lambda} \frac{\lambda^{x_1}}{x_{1}!} \cdot e^{-\lambda} \frac{\lambda^{x_2}}{x_{2}!} \cdots \cdots e^{-\lambda} \frac{\lambda^{x_6}}{x_{6}!}=e^{-6 \lambda} \frac{\lambda^{\sum_{i=1}^n x_i}}{\prod_{i=1}^6 x_{i}!}, \quad x_1, x_2, \cdots, x_6=0,1,2, \cdots

例设总体 $X \sim U(0, \theta), ~\left(X_1, X_2, L, X_n\right)$ 是取自上均匀分布总体 $X$ 的一个样本， $\theta>0$ 末知，求样本（ $X_1, X_2, \cdots, X_6$ ）的联合密度函数？解

\begin{aligned} f\left(x_1, x_2, \cdots, x_n ; \theta\right) & =f_{X_1}\left(x_1 ; \theta\right) f_{X_2}\left(x_2 ; \theta\right) \ldots \ldots f_{x_n}\left(x_n ; \theta\right) \\ & =\left\{\begin{array}{cc} \theta^{-n} & 0<x_1, x_2, \cdots, x_n<\theta \\ 0 & \text { 其它 } \end{array}\right. \end{aligned}

例设总体 $X \sim N\left(\mu, \sigma^2\right),\left(X_1, X_2, \cdots, X_n\right)$ 为取自该总体的一个样本，求样本 $\left(X_1, X_2, \cdots, X_n\right)$ 的联合密度函数？

解

f\left(x_1, x_2, \cdots, x_n ; \mu, \sigma^2\right)=\frac{1}{\left(2 \pi \sigma^2\right)^{\frac{n}{2}}} e^{-\frac{\sum\left(x_i-\mu\right)^2}{2 \sigma^2}},-\infty<x_i<+\infty

例设 $\left(X_1, X_2, \cdots, X_n\right)$ 是取自总体 $X$ 的一个样本， $X$ 的概率密度函数为

f(x, \theta)=\left\{\begin{array}{cc} \frac{2 x}{\theta^2} & 0<x<\theta \\ 0 & \text { 其余 } \end{array}\right.

试写出 $\left(X_1, X_2, \cdots, X_n\right)$ 的联合密度函数．联合密度函数为

f^*\left(x_1, x_2, \cdots, x_n, \theta\right)= \begin{cases}\frac{2^n x_1 \cdots x_n}{\theta^{2 n}} & 0<x_i<\theta, i=1,2, \cdots, n \\ 0 & \text { 其余 }\end{cases}