4._样本均值_样本方差_原点矩和中心矩

样本均值

假设有一组学生，身高分别是 $160,162,165,165,168$ 我要求他的平均身高，只要把这几个数加起来，除以个数即可，即

由此可得样本均值的定义：

样本均值 $\bar{x}=\frac{1}{n} \sum_{i=1}^n x_i$

样本分组均值 在分组样本场合，样本均值的近似公式为

其中 $k$ 为组数，$x_i$ 为第 $i$ 组的组中值，$f_i$ 为第 $i$ 组的频数．

如何理解样本分组后的均值？简单的理解，就是“加权平均数”，比如电视直播歌手比赛，专业评委和观众都可以打分，同样是打9分，专业评委的权重会比观众的权重要高，因此，此时计算分数，就使用了加权平均数。

例 某单位收集到 20 名青年人某月的娱乐支出费用数据：

则该月这 20 名青年的平均娱乐支出为

将这 20 个数据分组可得到如下频数频率表：

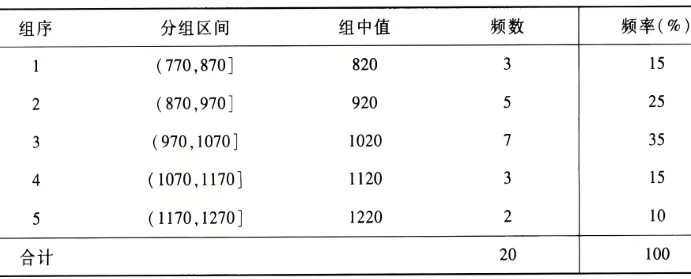
使用样本分组均值公式计算可得

我们看到两种计算结果不同．事实上，由于上式未用到真实的样本观测数据，因而给出的是近似结果．

样本方差与样本标准差

样本方差 $s^2=\frac{1}{n-1} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2$

样本标准差的观测值 $s=\sqrt{\frac{1}{n-1} \sum_{i=1}^n\left(x_i-\bar{x}\right)^2}$

为什么样本方差除以$n-1$而总体方差除以$n$？

在高中概率统计里学过方差，详见 此处, 样本方差计算公式里n-1与自由度有关系？那总体标准差为什么用n就没有自由度关系？

总体方差：总体方差是所有数据点与总体均值的偏差平方的平均值。如果总体数据是 $X_1, X_2, \ldots, X_n$ ，总体均值是 $\mu$ ，那么总体方差 $\sigma^2$ 的计算公式为：

这里除以 N 是因为总体方差是所有数据点的平均偏差平方。

样本方差：样本方差是样本数据点与样本均值的偏差平方的平均值。如果样本数据是 $x_1, x_2, \ldots, x_n$ ，样本均值是$\bar{x}$，那么样本方差 $s^2$ 的计算公式为：

样本方差是总体方差的无偏估计，那什么是无偏估计呢？

无偏估计：无偏估计是指估计量的期望值等于被估计的参数。在样本方差的计算中，使用 $n−1$ 作为分母可以使得样本方差的期望值等于总体方差，即

$E(s^2)=\sigma ^2$

这个性质对于统计推断非常重要，因为它保证了样本方差是一个可靠的总体方差估计。

综上所述，总体方差除以N是因为它是所有数据点的平均偏差平方，而样本方差除以 $n−1$ 是为了对总体方差进行无偏估计。

或者说，这里除以 $n-1$ 而不是 $n$ 的原因是样本方差需要对总体方差进行无偏估计。样本均值$\bar{x}$是从样本数据中计算出来的，它本身也存在一定的偏差。使用 $n-1$ 作为分母可以校正这个偏差，使得样本方差的期望值等于总体方差。

关于本题的数学推导，请参考 无偏向

如果从自由度的角度来讲，首先我们先从样本方差统计计算来看，因为一组样本值，由于其均值是一定的，即 $\bar{x}=(x_1+x_2...+x_n)/n$ ,由于有这个等式的存在，相当于增加了一个限制， 当$\bar{x}$固定了，看似有$n$个变量，但是真正能随便取值的是$n-1$ 个，因此样本方差计算时，它的自由度是$n-1$, 即要除以$n-1$ $n$ 。

那问题来了，为什么在计算整体（或称母本）方差时，而是除以$n$呢？ 还是自由度，当计算整体时，均值为 $\mu=(x_1+x_2...+x_n)/n$ 数据中$n$个可以自由变化的数字。在求解方差时，均值$\mu$ 看似增加了一个等式，其实是$n$个未知数，但是是$n+1$个等式，因此方差除以n

结论

样本方差是度量样本散布大小的统计量，使用广泛，在它的这个定义中， $n$ 为样本量，$\sum_{i=1}^n\left(x_i-\bar{x}\right)^2$ 称为偏差平方和，$n-1$ 称为偏差平方和的自由度。其含义是：在 $\bar{x}$ 确定后，$n$ 个偏差 $x_1-\bar{x}, x_2-\bar{x}, \cdots, x_n-\bar{x}$ 中只有 $n-1$ 个偏差可以自由变动，而第 $n$个则不能自由取值，因为 $\sum\left(x_i-\bar{x}\right)=0$ ．

样本偏差平方和有三个常用的表达式：

它们都可用来计算样本方差． 在分组样本场合，样本方差的近似计算公式为

其中 $x_i, f_i$ 分别为第 $i$ 个区间的组中值和频数， $\bar{x}$ 为分组均值里给出的样本均值近似值．

原点矩与中心矩

设 $x_1, x_2, \cdots, x_n$ 是样本，$k$ 为正整数，则统计量

称为样本 $k$ 阶原点矩，特别，样本一阶原点矩就是样本均值．

统计量

称为样本 $k$ 阶中心矩．

为什么要搞出原点矩和中心矩？如果说用样本估算总体，那我们希望估算的越准确越好。想象一下高等数学里泰勒展开 我们使用一阶导，二阶导，一直到n阶导拟合曲线。同样，如果样本期望和总体期望相同，样本方程和总体方差相同，样本3阶矩和总体3阶矩相同... 这不是最好的吗？ 关于原点矩和中心矩还有矩母函数请点击附录2

例设总体 $X$ 的均值 $E(X)=\mu$ ，方差 $D(X)=\sigma^2 ，\left(X_1, X_2, \cdots, X_n\right)$ 为取自该总体的一个 样本，则 (1) $\quad E(\bar{x})=\mu, D(\bar{x})=\frac{\sigma^2}{n}$ (2) $E\left(S^2\right)=\sigma^2, E\left(S_n^2\right)=\frac{n-1}{n} \sigma^2, n \geq 2$ (3) $\bar{X} \stackrel{P}{\longrightarrow} \mu, S^2=\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 \stackrel{P}{\rightarrow} \sigma^2, S_n^2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2 \stackrel{P}{\longrightarrow} \sigma^2$. 证 (1)

证 (2)

证 (3) 独立同分布的大数定律，即得 $\bar{X} \stackrel{P}{\longrightarrow} \mu$

所以 $S_n^2=\frac{1}{n} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2=\frac{1}{n} \sum_{i=1}^n X_i^2-\bar{X}^2 \stackrel{P}{\longrightarrow} \sigma^2+\mu^2-\mu^2=\sigma^2$

例 从某班级的英语期末考试成绩中，随机抽取 10 名同学的成绩（单位：分），分别为 $100,85,70,65,90,95,63,50,77,86$ ．求样本均值、样本方差及二阶原点矩．

解

二阶矩的重要性质

设总体 $X$ 具有二阶矩，即 $E(X)=\mu, D(X)=\sigma^2<+\infty, X_1, X_2, \cdots, X_n$ 为来自总体 $X$ 的样本， $\bar{X}$ 和 $S^2$ 分别是样本均值与样本方差，则 （1）$E(\bar{X})=E(X)=\mu$ ； （2）$D(\bar{X})=\frac{1}{n} D(X)=\frac{\sigma^2}{n}$ ； （3）$E\left(S^2\right)=D(X)=\sigma^2$ ．

证明： （1）$E(\bar{X})=E\left(\frac{1}{n} \sum_{i=1}^n X_i\right)=\frac{1}{n} \sum_{i=1}^n E\left(X_i\right)=\frac{n \mu}{n}=\mu$ ． （2）$D(\bar{X})=D\left(\frac{1}{n} \sum_{i=1}^n X_i\right)=\frac{1}{n^2} \sum_{i=1}^n D\left(X_i\right)=\frac{n \sigma^2}{n^2}=\frac{\sigma^2}{n}$ ． （3）因为 $E\left(X_i^2\right)=D\left(X_i\right)+E^2\left(X_i\right)=\sigma^2+\mu^2$ ，且 $E\left(\bar{X}^2\right)=D(\bar{X})+E^2(\bar{X})=\frac{\sigma^2}{n}+\mu^2$ ，所以

例 设总体 $X \sim B(m, \theta), X_1, X_2, \cdots, X_n$ 为来自该总体的简单随机样本， $\bar{X}$ 为样本均值，求 $E\left[\sum_{i=1}^n\left(X_i-\bar{X}\right)^2\right]$ ．

解 由上面性质可得 $E\left(S^2\right)=D(X)=m \theta(1-\theta)$ ，从而