4._二维离散型随机变量及其联合分布律 - Probability Theory and Mathematical Statistics

本文基础定义已经整合到联合分布函数里，详见此处

二维离散型随机变量及其联合分布律

设二维随机变量 $(X, Y)$ 仅可能取有限个值，则称 $(X, Y)$ 为二维离散型随机变量.

联合分布列定义

设二维随机变量 $P\left(X=x_i, Y=y_j\right)=p_{i j}$ , $i, j=1,2, \cdots$ 为二维随机变量 $(X, Y)$ 的联合分布律. 其中 $p_{i j} \geq 0, i, j=1,2, \cdots, \sum_i \sum_j p_{i j}=1$ .

二维随机变量 $(X,Y)$ 的联合分布律通常用表格法表示.

$图片$

注意：对离散型随机变量而言，联合概率分布表不仅比联合分布函数更加直观，而且能够更加方便地确定 $(X, Y)$ 取值于任何区域 $D$ 上的概率, 即

P((X, Y) \in D)=\sum_{\left(x_i, y_j\right) \in D} p_{i j} .

特别地，由联合概率分布可以确定联合分布函数：

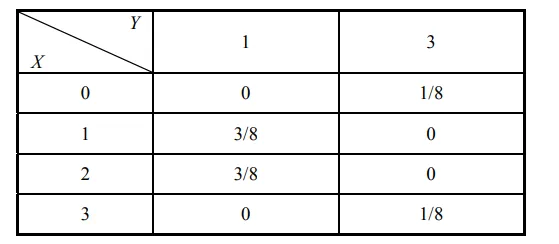
F(x, y)=P(X \leqslant x, Y \leqslant y)=\sum_{x_i \leqslant x, y_j \leqslant y} p_{i j} .

例 把一枚均匀硬币抛郑三次, 设 $X$ 为三次抛郑中正面出现的次数, 而 $Y$ 为正面出现次数与反面出现次数之差的绝对值, 求 $(X, Y)$ 的概率分布.

解 $(X, Y)$ 可取值 $(0,3)$ 、 $(1,1)$ 、 $(2,1)$ 、 $(3,3)$ 。

\begin{gathered} P(X=0, Y=3)=\left(\frac{1}{2}\right)^3=\frac{1}{8} \\ P(X=1, Y=1)=3 \times\left(\frac{1}{2}\right)^3=\frac{3}{8} \\ P(X=2, Y=1)=\frac{3}{8} \\ P(X=3, Y=3)=\frac{1}{8} \end{gathered}

故 $(X,Y)$ 分布概率表为 $图片$ {widht=500px}

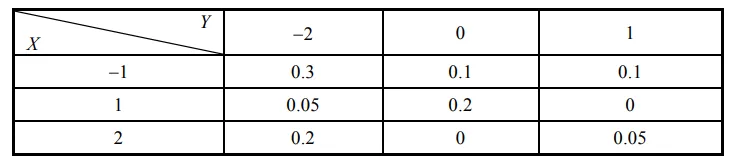
例 设二维随机变量的联合概率分布为 $图片$ {widht=500px} 求 $P(X \leqslant 1, Y \geqslant 0)$ 及 $F(0,0)$

解:

\begin{aligned} P(X \leqslant 1, Y \geqslant 0) & =P(X=-1, Y=0)+P(X=-1, Y=1)+P(X=1, Y=0)+P(X=1, Y=1) \\ & =0.1+0.1+0.2+0=0.4 . \\ F(0,0) & =P(X=-1, Y=-2)+P(X=-1, Y=0)=0.3+0.1=0.4 . \end{aligned}

例 有6个零件,其中优质品3个、正品(不含优质品)2个、次品1个.若从中任取3个用于设备安装,试求取出的3个零件中,含优质品数和正品数的联合分布律.

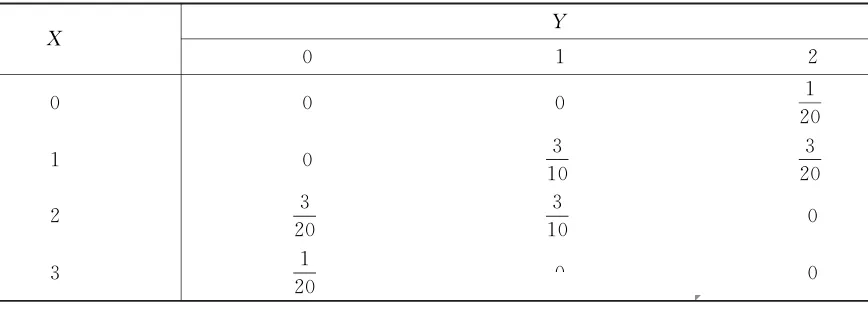
解设 $X,Y$ 分别表示取出的3个零件中含优质品和正品的个数,显然 $X=0,1,2,3;Y=0, 1,2,$ 故 $(X,Y)$ 的联合分布律为

p_{i j}=P\{X=i, Y=j\}=\frac{C_3^i C_2^j C_1^{3-i-j}}{C_6^3}(i=0,1,2,3 ; j=0,1,2)

上式只有当 $2 \leqslant i+j \leqslant 3$ 时有意义

当 $X=0$ 时， $\{X=0, Y=j\} (j=0,1)$ 均为不可能事件，

\begin{aligned} & P\{X=0, Y=0\}=P\{X=0, Y=1\}=0 \\ & P\{X=0, Y=2\}=\frac{C_2^2 C_1^1}{C_6^3}=\frac{1}{20} \end{aligned}

当 $X=1$ 时，

\begin{aligned} & P\{X=1, Y=0\}=0, \\ & P\{X=1, Y=1\}=\frac{C_3^1 C_2^1 C_1^1}{C_6^3}=\frac{3}{10}, \\ & P\{X=1, Y=2\}=\frac{C_3^1 C_2^2}{C_6^3}=\frac{3}{20} . \end{aligned}

当 $X=2$ 时，

\begin{aligned} & P\{X=2, Y=0\}=\frac{C_3^2 C_1^1}{C_6^3}=\frac{3}{20} \\ & P\{X=2, Y=1\}=\frac{C_3^2 C_2^1}{C_6^3}=\frac{3}{10} \end{aligned}

P\{X=2, Y=2\}=0 .

当 $X=3$ 时，

\begin{aligned} & P\{X=3, Y=0\}=\frac{C_3^3}{C_6^3}=\frac{1}{20} . \\ & P\{X=3, Y=1\}=P\{X=3, Y=2\}=0 . \end{aligned}

故 $(X, Y)$ 的联合分布律如表 3－4 所示．表 3－4 $图片$ {width=500px}

例 设 $(X, Y)$ 的分布律为 $图片$ 求：（1） $P\{X=0\}$ ；（2） $P\{Y \leqslant 2\}$ ；（3） $P\{X<1, Y \leqslant 2\}$ ；（4） $P\{X+Y=2\}$ ．

解：分析利用联合分布律求概率公式为

P\{(X, Y) \in G\}=\sum_{\left(x_i, y_j\right) \in G} p_{i j}

解（1） $P\{X=0\}=P\{X=0, Y=1\}+P\{X=0, Y=2\}+P\{X=0, Y=3\}$

=0.1+0.1+0.3=0.5 ;

(2) $P\{Y \leqslant 2\}=P\{X=0, Y=1\}+P\{X=0, Y=2\}+P\{X=1, Y=1\}+P\{X=1, Y=2\}$ $=0.1+0.1+0.25+0=0.45 ;$ (3) $P\{X<1, Y \leqslant 2\}=P\{X=0, Y=1\}+P\{X=0, Y=2\}=0.1+0.1=0.2$ ; (4) $P\{X+Y=2\}=P\{X=0, Y=2\}+P\{X=1, Y=1\}=0.1+0.25=0.35$ .