引入
例① 联合分布是指一个事件受到多个因素控制,比如判断一个孩子的健康需要考虑:身高和体重两个维度,我们就说“身高”和“体重”这两个参数联合起来共同决定了孩子的健康程度,后面还会有一个边缘分布,他只有一个参数决定。
例② 射靶,如果以靶心为原点建立直角坐标系,那么靶点落的位置则是有(X,Y)共同决定。
上面这两个引例都告诉我们,现实世界很多事情是由多个参数来决定,因此,引入多维联合分布。
二维联合分布
定义1 如果 X=X(ω),Y=Y(ω) 是定义在同一个样本空间 Ω={ω} 上的两个随机变量,则称 (X(ω),Y(ω))=(X,Y) 为定义在 Ω 上的二维随机变量。
定义2 设 (X,Y) 是二维随机变量, 对任意实数 x、y, 二元函数
F(x,y)=P(X⩽x,Y⩽y) 称为二维随机变量 (X,Y) 的分布函数或随机变量 X 和 Y 的联合分布函数.
离散型联合分布函数求法
例袋中有一个红色球,两个黑色球,三个白球,现有放回的从袋中取两次,每次取一球,以 X,Y,Z 分别表示两次取球的红,黑,白球的个数.
(1)求 P{X=1∣Z=0} ;
(2)求二维随机变量 (X,Y) 的概率分布.
解(1)在没有取白球的情况下取了一次红球,利用样本空间的缩减法,相当于只有 1 个红球, 2 个黑球有放回摸两次,其中摸一个红球的概率,所以
P{X=1∣Z=0}=32C21×2=94. (2)X,Y 取值范围为 0,1,2 ,故
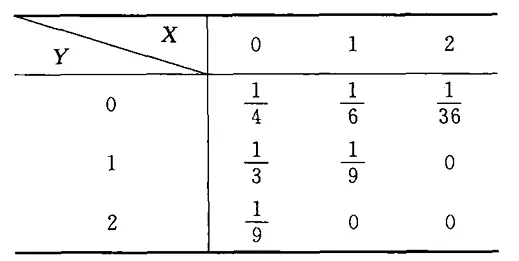
P{X=0,Y=0}=62C31×C32=41,P{X=1,Y=0}=62C21×C31=61,P{X=2,Y=0}=621=361,P{X=0,Y=1}=62C21×C21×C31=31,P{X=1,Y=1}=62C21×C21=91,P{X=2,Y=1}=0,P{X=0,Y=2}=62C21×C21=91,P{X=1,Y=2}=0,P{X=2,Y=2}=0. 最后列表可得
连续型联合分布的数学定义
联合分布用数学语言可以表示为:
对于二维随机变量 ξ=(X,Y), 如果存在非负函数 p(x,y)(−∞<x<∞,−∞<y<∞), 使对任意 a<b,c<d 及 D={(x,y):a<x<b,c<y<d} 有
P((X,Y)∈D)=∬Dp(x,y)dxdy 则称随机变量 ξ=(X,Y) 为连续型的, 并称 p(x,y) 为 ξ 的分布密度, 也称 p(x,y) 为 (X,Y) 的联合分布密度 (简称联合密度)。
续型随机变量属于更一般的平面子集 D 的概率为
P((X,Y)∈D)=∬Dp(x,y)dxdy 联合分布的几何解释
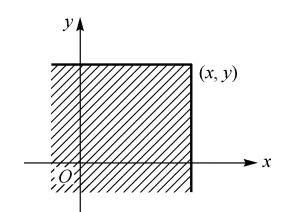
我们容易给出分布函数的几何解释:如果把二维随机变量 (X,Y) 看成是平面上随机点的坐标,那么分布函数 F(x,y) 在 (x,y) 处的函数值就是随机点 (X,Y) 落在直线 X=x 的左侧和直线 Y=y 的下方的无穷矩形域内的概率,如下图3-1所示.
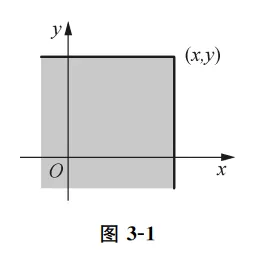
对于联合分布,用通俗语言理解是,例如用X表示学生的身高,用Y表示学生的体重,那么联合分布 F(170,60)=P(X⩽170,Y⩽60) 表示的是:身高低于170cm,体重低于60kg的学生的分布。这句话还可以正面解释为求:身高在(−∞,170) 与 体重在 (−∞,60) 的学生的分布。
因此,给出一个点(X,Y),求他的联合分布,其实表示的该点“左边下边”所围成的面积(参考图3-1阴影部分面积)。
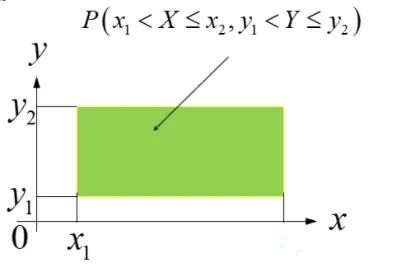
根据以上的几何解释,借助于图3-2,我们可以计算出随机点 (X,Y) 落在矩形域 {(x,y)∣x1<x⩽x2,y1<y⩽y2} 内的概率为
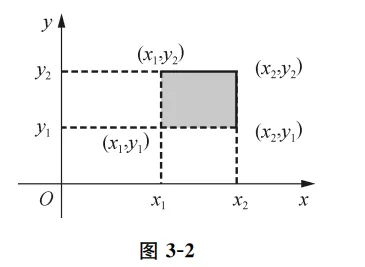
P{x1<X⩽x2,y1<Y⩽y2}=F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1). 对于图3-2,也可以用学生身高体重解释。用X表示学生的身高,用Y表示学生的体重,那么联合分布 P{160<X⩽170,50<Y⩽60}=F(170,60)−F(170,50)−F(160,60)+F(160,50) 等式左边表示的是求学生身高在160∼170 和 体重在50∼60 之间的人数,他等于身高体重在 (170,60)以下的人数减去 身高170以下的人数,再减去体重60以下的人数,注意此时对(160,50)以下的人数减了两次,所以还要再补上一次,因此最后加上(160,50)
看懂联合密度的密度图
我们在一维平面里说过,概率密度(a,b)曲线下的面积是事件发生在(a,b)间的频率,详见此处, 那么如何理解二维概率密度呢?
首先,我们要明白,二维概率事件是由3个参数决定:比如射靶,我们说“射在(1,2)的概率为0.01”,那么这里就有X=1,Y=2,Z=0.01三个参数
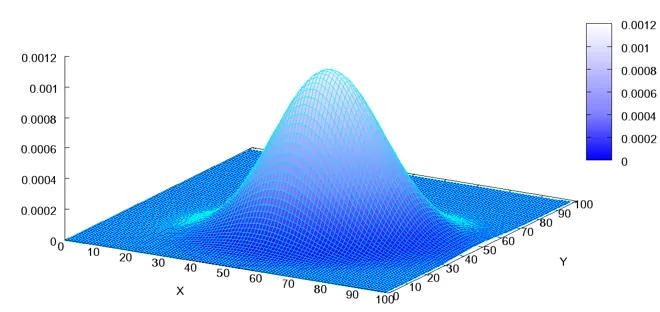
因此,如果把密度函数画在坐标系里,他需要是三维空间,如下图:
 {width=400px}
{width=400px}
这个图形很像农民带的草帽,我们通常称呼这个图形为“草帽”图形。因为密度函数必须大于等于零,所以这个草帽可以认为为平底的,又因为所有射靶所有的概率最多为1,因此,这个概率的体积最大只能为1.
理解二维密度函数图像
如果我们从俯视图的视角从下看这个草帽,可以发现他的定义域D就是一个二维平面。
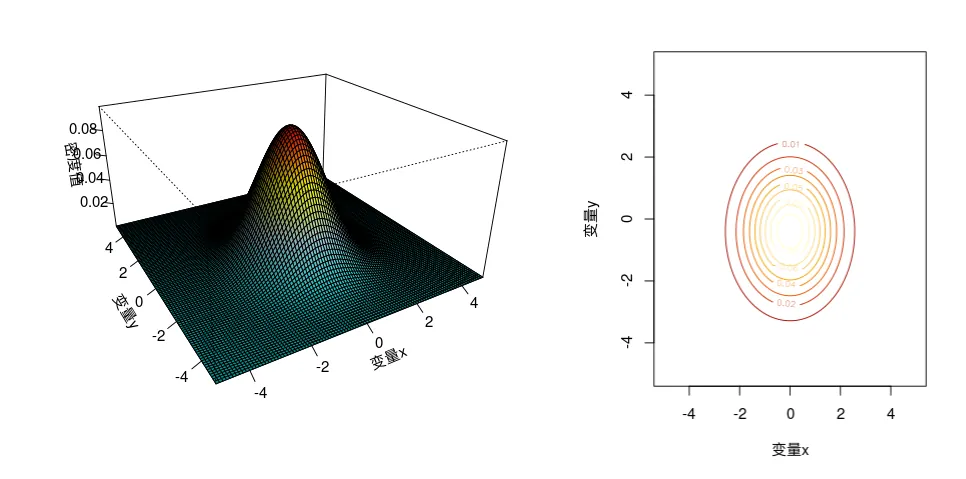 {width=400px}
{width=400px}
想想一下我们用一把刀沿着X,Y 切开草帽,因为分布函数的定义为 F(x,y)=P(X⩽x,Y⩽y)=∫−∞x∫−∞yp(x,y)dxdy ,所以,我们取的西瓜就是左边下边的那一部分。
如果把二维随机变量 (X,Y) 视为平面上随机点的坐标, 那么, 分布函数 F(x,y)在点 (x,y) 处的函数值就是随机点 (X,Y) 落在直线 X=x 的左侧和直线 Y=y 的下方以 (x,y) 为顶点的无穷直角区域内的概率, 如图所示.
联合分布函数得性质
性质1: 0≤F(x,y)≤1
这个性质很好理解,分布函数反映到是概率,概率总是大于等于0小于等于1.
单调性2: F(x,y) 关于 x 和 y 均为单调非减函数, 即
对任意固定的 y ,当 x2>x1 时, F(x2,y)⩾F(x1,y) ;
对任意固定的 x, 当 y2>y1 时, F(x,y2)⩾F(x,y1).
有界性3:对任意实数 x、y ,有 0⩽F(x,y)⩽1 ,且
对任意固定的 y ,有 F(−∞,y)=0 ,
对任意固定的 x, 有 F(x,−∞)=0,
F(−∞,−∞)=0,F(+∞,+∞)=1.
右连续性4 F(x,y) 关于 x 和 y 均为右连续, 即
F(x,y)=F(x+0,y),F(x,y)=F(x,y+0). 非负性5 对于任意 x1<x2、y1<y2 ,下述不等式成立:
F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1)⩾0. 注意:对任意的 x1<x2,y1<y2 ,有矩形公式
P(x1<X≤x2,y1<Y≤y2)=F(x2,y2)−F(x1,y2)−F(x2,y1)+F(x1,y1). 参考下图
例题
例 (离散型)下图 所示的二维离散型随机向量 X=(X1,X2) 的概率分布为
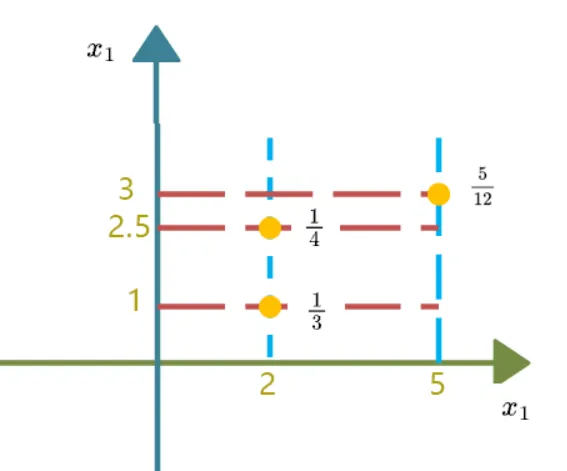 {width=300px}
解:
{width=300px}
解:
P(X1=2,X2=1)=1/3P(X1=2,X2=2.5)=1/4P(X1=5,X2=3)=5/12...(2.1) 从图上看出, X1 的可能值为 2 和 5,X2 的可能值为 1,2.5 和 3 . 故形式上看, X=(X1,X2) 应有 6组可能值,即
(2,1),(2,2.5),(2,3),(5,1),(5,2.5),(5,3)
X的概率分布告诉我们, 实际上只有第 1,2,6 组是真正的可能值, 但这并无关系:对一组不可能的值,只要把它的概率定为 0 就行了.
例(连续型)设二维随机变量 (X,Y) 的分布函数为
f(x,y)={cosxcosy,0<x,y<2π0, else (1) 试求 X,Y 联合分布函数.
(2) 试求 P(0≤X≤4π≤Y≤2π).
解(1)根据限制域的特点,我们很显然要做分类讨论。 以下设待求函数为 F(u,v). 但是,这是完全没有必要一个一个情况代的。因为只需要在图上标出积分域, 就自然而然清楚需要怎么积分了。
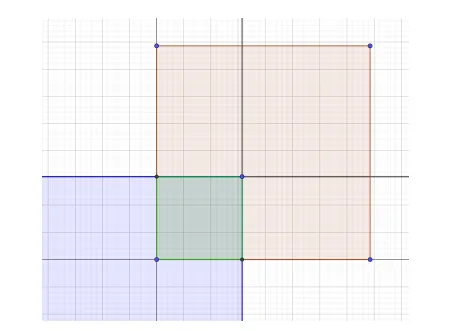 (a) u,v 中有一个小于 0 (包括均小于 0). 很明显, 只要有这种情况存在, 积分域内就没有非 0 的情况.
(b) u,v 均介于 0,2π 之间. 那么 F(u,v)=∫0u∫0vcosxcosydxdy=sinusinv.
(c) u,v 中有一个大于 2π, 另一个介于 0,2π 之间. 那么 F(u,v)=∫01∫0vcosxcosydxdy= sinv 或同理, sinu.
(d) u,v 均大于 2π. 显然 F(u,v)=1.
(a) u,v 中有一个小于 0 (包括均小于 0). 很明显, 只要有这种情况存在, 积分域内就没有非 0 的情况.
(b) u,v 均介于 0,2π 之间. 那么 F(u,v)=∫0u∫0vcosxcosydxdy=sinusinv.
(c) u,v 中有一个大于 2π, 另一个介于 0,2π 之间. 那么 F(u,v)=∫01∫0vcosxcosydxdy= sinv 或同理, sinu.
(d) u,v 均大于 2π. 显然 F(u,v)=1.
综上, F(x,y)=⎩⎨⎧0,x≤0 or y≤0sinxsiny,0<x,y<2πsinx,0<x<2π,y≥2π..(2) 只需套公式即可. siny,x≥2π,0<y<2π1,x,y≥2π
分布函数和密度函数的转化
已知分布函数求密度函数
例 设二维随机变量 (X,Y) 的联合分布函数为
F(x,y)={1−3−x−3−y+3−x−y,0,x⩾0,y⩾0 其他. 则二维随机变量 (X,Y) 的联合密度 φ(x,y) 为 .
解 可以验证这是二维连续型随机变量的分布函数,由公式:
φ(x,y)=∂x∂y∂2F 有
∂x∂F=3−xln3−3−x−yln3∂x∂y∂2F=3−x−y(ln3)2 故 φ(x,y)={3−x−y(ln3)2,0,x⩾0,y⩾0 其他.
已知密度函数求分布函数
例 设二维随机变量 (X,Y) 的概率密度为
f(x,y)={6x,0,0⩽x⩽y⩽1 其他. 则 P{X+Y⩽1} 是多少
解 由题意作图 所示
P{X+Y⩽1}=∬x+y⩽1f(x,y)dxdy=∫021dx∫x1−x6xdy=∫0216x(1−2x)dx=41. 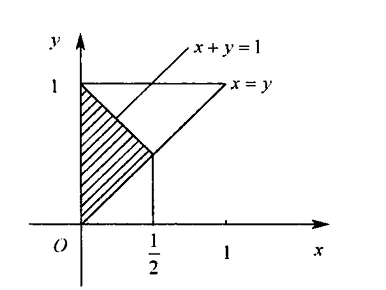



 {width=400px}
{width=400px} {width=400px}
{width=400px}

 {width=300px}
解:
{width=300px}
解: (a) 中有一个小于 0 (包括均小于 0. 很明显, 只要有这种情况存在, 积分域内就没有非 0 的情况.
(b) 均介于 之间. 那么 .
(c) 中有一个大于 , 另一个介于 之间. 那么 或同理, .
(d) 均大于 . 显然 .
(a) 中有一个小于 0 (包括均小于 0. 很明显, 只要有这种情况存在, 积分域内就没有非 0 的情况.
(b) 均介于 之间. 那么 .
(c) 中有一个大于 , 另一个介于 之间. 那么 或同理, .
(d) 均大于 . 显然 .