引入
对于初学者刚学习二维均匀分布时,最容易产生的一个疑问是:为什么要学习均匀分布?他有什么用?
对于均匀分布必须结合本课程后面统计学来看。比如看一个简单的例子,雨点均匀的落在盘子里,基本上不需要额外的知识,我们本能的就能感觉,雨点落在每个地方的几率是一样的,假设盘子是正方形,其半径为a,那么正方形的面积就是a2,这样,每一点的概率就是a21,
同样的,如果盘子是圆,半径为r,盘子的面积就是πr2,那么每一点的概率就是πr21,由此推出如果盘子的面积为S,每一点的概率就是S1. 这种推理是正确的,但是我们需要更抽象这种定义。正方形,圆都是比较简单的图像,如果盘子的图形是各种不规则图形呢?这时就需要采用微积分的思想来计算面积。
还必须注意一点:像雨点落在盘子上这种分布是很容易想到是二维均匀分布的,但是在实际中,我们拿到一个事件可能并不容易得到他是一个什么分布,比如车轮在马路上行驶,已知车轮面积是S,每一点的概率是S1,那么,我们就可以倒推过去,说这个车轮是二维均匀分布。
二维均匀分布
根据多维随机变量的性质,假设f(x,y)为二维均匀分布密度函数,那么他的密度函数应该满足下面两个条件:
性质① f(x,y)≥0
性质② ∫−∞+∞∫−∞+∞f(x,y)dydx=1
既然叫做“均匀分布”,我们有理由相信,密度函数在各点的密度应该相等(否则就不可能叫均匀分布了,比如雨滴落在圆板上,圆板上各点受到的雨滴几率相等),因此,我们假设二维均匀密度函数为
f(x,y)={c,0,x2+y2≤r2, 其他. 现在,我们要计算c的值为多少。根据密度函数“性质②”应该有
∫−∞+∞∫−∞+∞cdydx=1 ,其中,定义域为 x2+y2≤r2 的圆,
这是一个简单的二重积分, 因为c是常数,可以直接提到外面,即
c∫−∞+∞∫−∞+∞dydx=1 ,dydx 是面积元,积分后得 cπr2=1 ,所以
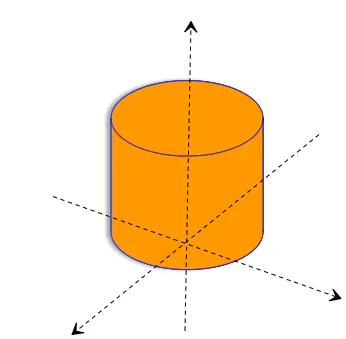
c=πr21 ,即下图圆柱的高为πr21
 {width=200px}
{width=200px}
因此圆盘的二维均匀密度函数为
f(x,y)=⎩⎨⎧πr21,0,x2+y2≤r2, 其他. 在上面举的例子里,雨滴随机的落在半径为r的圆上,从几何概率的角度也可以猜想,各个点密度为πr21,即面积的倒数。(同理可以推出,一维是长度的倒数,二维是面积的倒数,三维是体积的倒数)
下面给出具体的定义。
定义1 设二维随机变量 (X,Y) 的联合密度函数为
f(x,y)={A1,0,(x,y)∈G, 其他. 其中 G 是平面 xoy 上的某个区域, A 为区域的面积, 则称随机变量 (X,Y) 服从区域 G 上的二维均匀分布.
二维均匀分布所描述的随机现象就是向平面区域 G 中随机投点, 如果该点坐标 (X,Y) 落在 G 的概率只与 G 的面积有关, 而与 G 的位置无关, 这就是均匀分布。
例设 (X,Y) 服从区域 D 上的均匀分布,其中 D:x⩾y,0⩽x⩽1,y⩾0 ,求 P{X+Y⩽1} .
分析:拿到均匀分布,最主要是画出图,如下
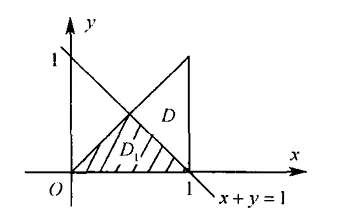 因为均匀分布的密度函数就是面积的,就本题而言就是需要求出上图阴影面积。
因为均匀分布的密度函数就是面积的,就本题而言就是需要求出上图阴影面积。
解法一 因为 D 的面积 A=21 ,所以 (X,Y) 的概率密度为
则
f(x,y)P{X+Y⩽1}={2,0,(x,y)∈D 其他 =∬x+y⩽1f(x,y)dxdy=∬D12dxdy( 如图 3−2.7)=2×41=21. 解法二 可利用几何概率计算
P{X+Y⩽1}=S(D)S(D1)=21. 点评 二维均匀分布求概率有时候利用几何概型来计算,更加简便.
例题
例 设 (X,Y) 服从单位圆域 x2+y2⩽4 上的均匀分布, 求 (X,Y) 的概率密度及 P(0<X<1,0<Y<1).
解 圆域 x2+y2⩽4 的面积 A=4π, 故 (X,Y) 的概率密度为
f(x,y)={4π1,0,x2+y2⩽4 其他 , G 为由不等式 0<x<1 和 0<y<1 所确定的区域, 所以
P(0<X<1,0<Y<1)=∬Gf(x,y)dxdy=∫01dx∫014π1dy=4π1. 例设 D 为平面上以原点为圆心、以 r 为半径的圆内区域, 如今向该圆内随机投点, 其坐标 (X,Y) 服从 D 上的二维均匀分布,其密度函数为
p(x,y)={πr21,0,x2+y2⩽r2,x2+y2>r2. 试求概率 P(∣X∣⩽r/2).
解 p(x,y) 的非零区域与 {∣X∣⩽r/2} 的交集部分见图, 因此所求概率为
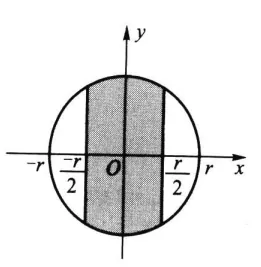
P(∣X∣⩽2r)=∫−r/2r/2∫−r2−x2r2−x2πr21dydx=πr21∫−r/2r/22r2−x2dx=πr21[xr2−x2+r2arcsinrx]−r/21/2=πr21(rr2−4r2+2r2arcsin21)=π1(23+3π)=0.609. 例 设 (X,Y) 服从区域 G 上的均匀分布,其中 G={(x,y):0<x<1 且 0<y<2x}
(1)写出f(x,y)的联合密度函数
(2)计算概率
解:(1)因区域的面积为 1 ,故由定义得联合密度函数为: f(x,y)={10(x,y)∈G, 其他.
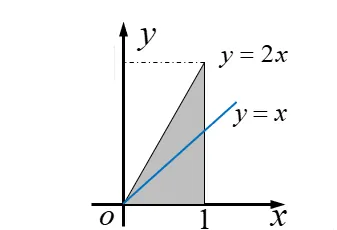 (2) 所求概率为
(2) 所求概率为
P(Y≤X)=P((X,Y)∈D)=∬Df(x,y)dx dy=∬D1 dx dy=SD=21 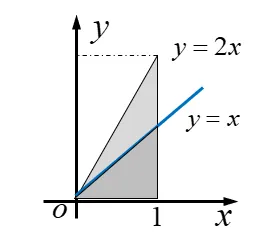
概率的尽头是微积分,比如下面这个例题,均匀分布就是计算面积,而微积分本质就是计算面积,所以,均匀分布可以计算复杂几何体面积。
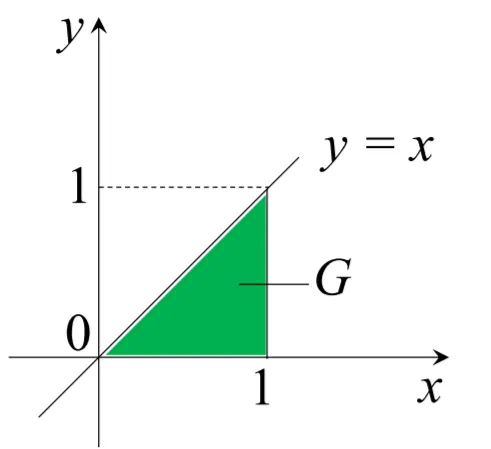
例 设 (X,Y)∼G 上的均匀分布,其中
G={(x,y)∣0≤y≤x,0≤x≤1} (1)求 f(x,y) ;
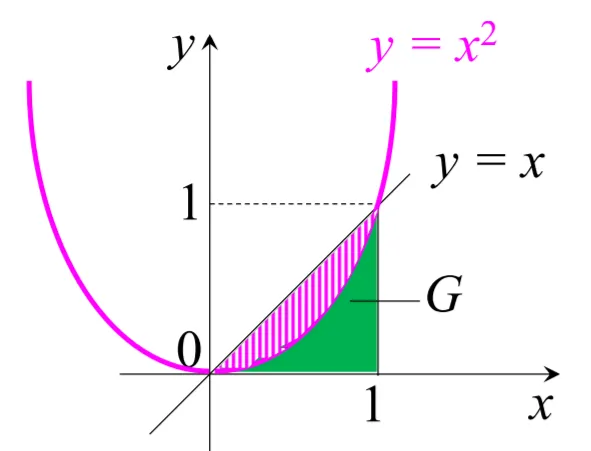
(2)求 P(Y>X2);
(3)求 (X,Y) 在平面上的落点到 y 轴距离小于 0.3 的概率
解:画出积分区域
(1)
 {width=300px}
{width=300px}
G={(x,y)∣0≤y≤x,0≤x≤1}f(x,y)={2,0,0≤y≤x,0≤x≤1 其他 (2)
 {width=200px}
{width=200px}
P(Y>X2)=∫01dx∫x2x2dy=31 (3)
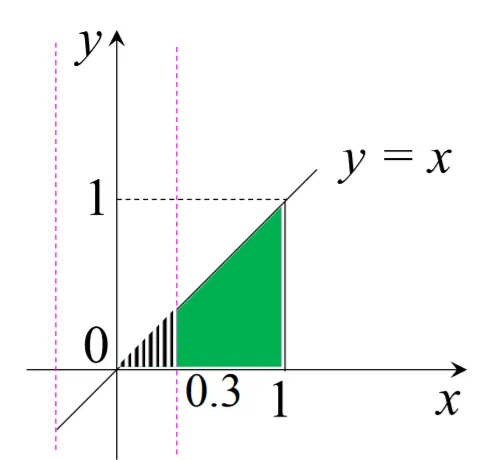
==P(∣X∣<0.3)P(−0.3<X<0.3)2⋅21⋅(0.3)2=0.09 二维均匀分布涉及到二重积分的计算,如果要查看二重积分,请点击 此处
 {width=200px}
{width=200px} 因为均匀分布的密度函数就是面积的,就本题而言就是需要求出上图阴影面积。
因为均匀分布的密度函数就是面积的,就本题而言就是需要求出上图阴影面积。
 (2) 所求概率为
(2) 所求概率为
 {width=300px}
{width=300px} {width=200px}
{width=200px}