我们已经成功地讨论了两个相互独立的随机变量之和的分布．在此基础上，我们来考察三个或更多个相互独立的随机变量之和的分布。设 Xi 是概率密度函数为 fXi 的随机变量． 如果 U 和 V 是两个相互独立的随机变量，那么 fU+V(z)=(fU∗fV)(z) ．由此能不能求出 fX1+X2+X3 ，或者更一般的 fX1+⋯+Xn ？
答案是肯定的！
定理： （独立的随机变量之和）设 X1,X2⋯,Xn 是相互独立的随机变量，它们的概率密度函数分别是 fX1,fX2,⋯,fXn ，那么
fX1+⋯+Xn(z)=(fX1∗fX2∗⋯∗fXn)(z) 其中
(f1∗f2∗⋯∗fn)(z)=(f1∗(f2∗⋯∗(fn−2∗(fn−1∗fn))⋯))(z) 我们已经证明了卷积是可交换的，也就是说 f∗g=g∗f ．另外，卷积还满足结合律：(f∗g)∗h=f∗(g∗h) ．记住，卷积要用两个函数作为输入，并返回一个函数作为输出．我们不能直接对三个函数求卷积．所以，如果给出了 f∗g∗h ，就要小心地解释这是什么意思．因为卷积需要两个输入，所以这里有两种解释方法：f∗g∗h等于 (f∗g)∗h 或者 f∗(g∗h) ．幸运的是，因为卷积满足结合律，所以这两个表达式是相等的，写哪个都可以。虽然我们可以直接证明结合律，但没必要这样做．原因在于，我们只在乎关于概率密度函数的卷积定理，而且有个很好的技巧能让我们更自由地使用结合律．
定理证明：我们只考察 n=3 的情形，一般情形下的结果可以类似地证明。
那么，现在就来考察 Z=X1+X2+X3 ．我们把这个式子写成 Z=(X1+X2)+ X3 ．这样做的好处是，对于两个相互独立的随机变量，它们的和的概率密度函数就是它们概率密度函数的卷积．（注意，因为 X3 独立于 X1 和 X2 ，所以 X3 与它们的和也是相互独立的．）于是有
fZ(z)=(fX1+X2∗fX3)(z) 现在，由定理 10．1．2 可知，fX1+X2=fX1∗fX2 ．把它代入上式，就得到了
fZ(z)=((fX1∗fX2)∗fX3)(z) 当然，我们也可以写成 Z=X1+(X2+X3) ，而不是 Z=(X1+X2)+X3 ．在这种情况下，首先得到的是
fZ(z)=(fX1∗fX2+X3)(z) 利用 fX2+X3=fX2∗fX3 ，有
fZ(z)=(fX1∗(fX2∗fX3))(z) 如果继续沿着这种思路论证下去，就不难看出如何对卷积进行分组并不重要。我们甚至可以颠倒函数的次序，比如 X1+X2+X3=X2+X3+X1（等等）．
对于四个相互独立的随机变量，可以写成 X1+(X2+(X3+X4)) ，这会给出概率密度函数 fX1∗(fX2∗(fX3∗fX4)) ．
上述过程是我最喜欢的论述之一。注意，这里完全没有求积分或求和。我们先分组，接着探讨了由此带来的结果，并最终得到了答案．我把这种方法称为分组证明法，其他相关示例，请参阅 A． 3 节．
回到 10.2 节的骰子问题．接下来的问题将会展示一个真正的精彩视角．独立地拋掷三颗骰子，我们可以求出得到数字的 PDF．我们知道掷一颗骰子以及掷两颗骰子所得数字的概率密度函数，所以现在只需要求出卷积．遗憾的是，说起来容易做起来难，原因是这里的代数运算有些杂乱。
我们把抛掷三颗骰子的头痛问题留给你自己来解决，现在继续考虑掷四颗骰子的情况．考察四颗骰子的好处在于，我们可以采用另一种还没有被提到过的分组方法．更好的解决方案是将四个变量分组为 (X1+X2)+(X3+X4) ，而不是 X1+(X2+(X3+X4)) ．为什么这种做法会更好呢？现在仍然要进行三次加法运算，不是吗？是的，但也不对！再看一下第二种分组方法：(X1+X2)+(X3+X4) ．注意，第一个加法和最后一个加法是相同的，概率密度函数 fX1+X2=fX1∗fX2 就等于 fX3+X4=fX3∗fX4 ．所以，虽然从技术上看，这里要进行三次加法运算，但其中两次是相同的．这远好于 X1+(X2+(X3+X4)) 的分组方式，因为后者涉及三个完全不同的加法运算。
如果考察八个相互独立且同分布的随机变量的和，这种优势就更明显了．这个和可以写成
((X1+X2)+(X3+X4))+((X5+X6)+(X7+X8)), 从而减少大量运算．两个变量的加法要进行四次，然后把得到的和相加两次，接着再把两个结果相加．换句话说，我们要计算三种不同的卷积，但是如果采用下列分组方式
X1+(X2+(X3+(X4+(X5+(X6+(X7+X8)))))), 就必须算出七个不同的卷积．这显然没有第一种分组方式好．
从某种意义上说，上述启示并不重要，但这种观点是不正确的．没错，如果不使用巧妙的分组方法，我们也可以算出 PDF，但这只会增加麻烦。我的人生目标之一就是尽量减少烦琐乏味的代数运算．分组是一种很好的方法，可以让代数运算更容易处理。
为了看出这一点，我们来考察独立地抛掷四颗骰子所得到的数字之和．让 X1 ， X2, X3 和 X4 分别表示这四颗骰子掷出的数字．我们知道这几个变量服从的分布，还知道 X1+X2 和 X3+X4 的概率密度函数
fX1+X2(u)=fX3+X4(u)=⎩⎨⎧36u−13613−u0 若 u∈{2,⋯,7} 若 u∈{7,⋯,12} 其他. 现在就可以计算掷出的数字之和为 4,5,6,⋯,24 的概率．
设 Z=X1+X2+X3+X4 ，我们有 fZ(z)=(fX1+X2∗fX3+X4)(z) ，其中，对于等号右端的两个非 0 的概率密度函数，它们的输入都只能是介于 2 和 12 之间的值．例如
fZ(6)=k=2∑12fX1+X2(k)fX3+X4(6−k)=k=2∑4fX1+X2(k)fX3+X4(6−k)=362−1364−1+363−1363−1+364−1362−1=129610=6485 类似地，我们还能求出其余 20 个函数值．这比把 64=1296 种可能的结果全都写出来要好得多．图 10－3 显示了其结果．
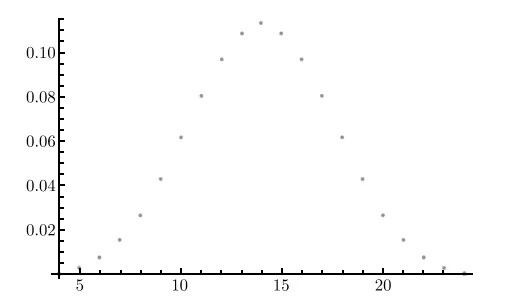如果你听说过中心极限定理, 那就透过它看看图 10-3 —— 你应该能开始看到钟形曲线, 或者开始想到高斯分布了.