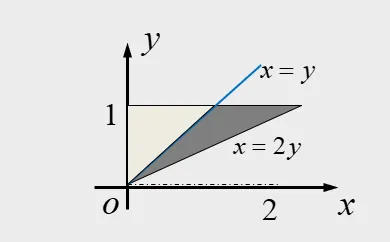本文基础定义已经整合到 联合分布函数里,详见 此处
二维连续型随机变量及其联合密度函数
设二维随机变量 (X,Y) 的联合分布函数为 F(x,y) ,如果存在二元非负实值函 数 f(x,y) ,使得对任意的 (x,y)∈R2 有
F(x,y)=P(X≤x,Y≤y)=∫−∞x∫−∞yf(u,v)dudv=∬Dyf(u,v)dudv 则称 (X,Y) 为二维连续型随机变量,称 f(x,y) 为二维连续型随机变量 (X,Y) 的联合 (概率) 密度函数.
定义n维随机变量与联合密度
设 n 维随机变量 (X1,X2,⋯,Xn) 的联合分布函数为 F(x1,x2,⋯,xn) ,如果存在一个 n 元非负 函数 f(x1,x2,⋯,xn) ,使得对任意的 (x1,x2,⋯,xn)∈Rn 有
F(x1,x2,⋯,xn)=∫−∞x1∫−∞x2⋯∫−∞xnf(u1,u2,⋯,un)du1du2⋯dun 成立,则称 (X1,X2,⋯,Xn) 为 n 维连续型随机变量, f(x1,x2,⋯,xn) 为 n 维连续型随机变量 (X1,X2,⋯,Xn) 的联合 (概率) 密度函数。
联合密度函数的性质
设 f(x,y) 为二维连续型随机变量 (X,Y) 的联合密度函数,则
(1) 非负性 f(x,y)≥0,−∞<x,y<+∞;
(2)规范性 ∫−∞+∞∫−∞+∞f(x,y)dx dy=1.
(3)任意一条平面曲线 L ,有 P((X,Y)∈L)=0 ;
(4)F(x,y) 为连续函数,在 f(x,y) 的连续点处有
∂x∂y∂2F(x,y)=f(x,y); (5)对 xoy 平面上任意一区域 D ,有
P((X,Y)∈D)=∬Df(x,y)dx dy 联合分布的几何解释
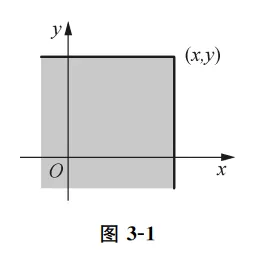
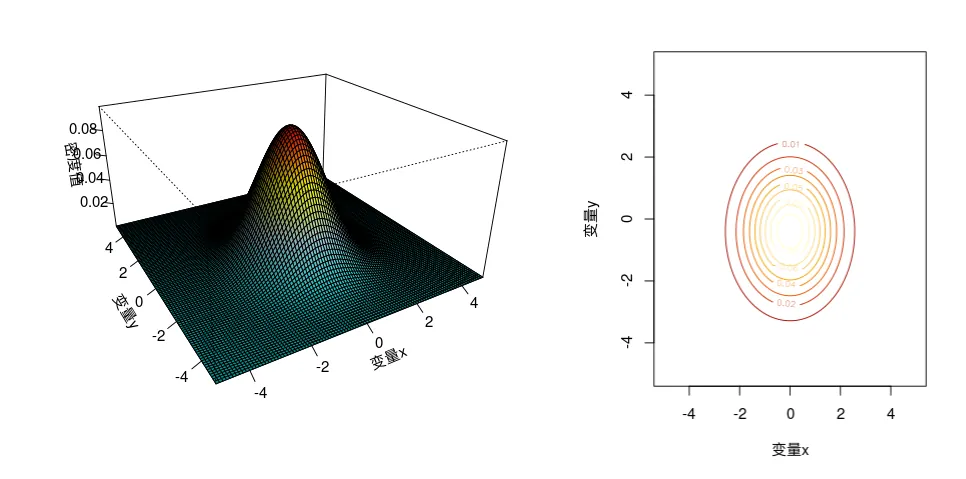
我们容易给出分布函数的几何解释:如果把二维随机变量 (X,Y) 看成是平面上随机点的坐标,那么分布函数 F(x,y) 在 (x,y) 处的函数值就是随机点 (X,Y) 落在直线 X=x 的左侧和直线 Y=y 的下方的无穷矩形域内的概率,如下图3-1所示.
对于联合分布,用通俗语言理解是,例如用X表示学生的身高,用Y表示学生的体重,那么联合分布 F(170,60)=P(X⩽170,Y⩽60) 表示的是:身高低于170cm,体重低于60kg的学生的分布。这句话还可以正面解释为求:身高在(−∞,170) 与 体重在 (−∞,60) 的学生的分布。
因此,给出一个点(X,Y),求他的联合分布,其实表示的该点“左边下边”所围成的面积(参考图3-1阴影部分面积)。
根据以上的几何解释,借助于图3-2,我们可以计算出随机点 (X,Y) 落在矩形域 {(x,y)∣x1<x⩽x2,y1<y⩽y2} 内的概率为
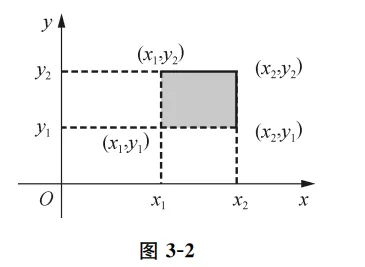
P{x1<X⩽x2,y1<Y⩽y2}=F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1). 对于图3-2,也可以用学生身高体重解释。用X表示学生的身高,用Y表示学生的体重,那么联合分布 P{160<X⩽170,50<Y⩽60}=F(170,60)−F(170,50)−F(160,60)+F(160,50) 等式左边表示的是求学生身高在160∼170 和 体重在50∼60 之间的人数,他等于身高体重在 (170,60)以下的人数减去 身高170以下的人数,再减去体重60以下的人数,注意此时对(160,50)以下的人数减了两次,所以还要再补上一次,因此最后加上(160,50)
看懂联合密度的密度图
我们在一维平面里说过,概率密度(a,b)曲线下的面积是事件发生在(a,b)间的频率,详见此处, 那么如何理解二维概率密度呢?
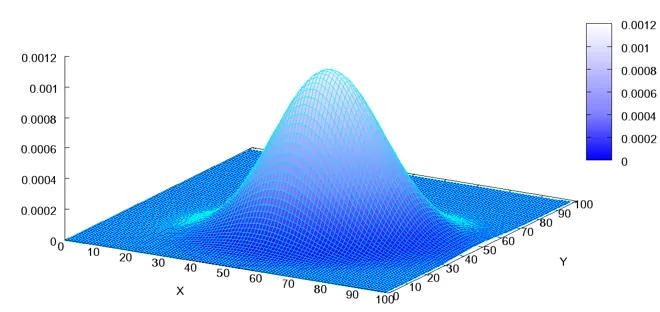
首先,我们要明白,二维概率事件是由3个参数决定:比如射靶,我们说“射在(1,2)的概率为0.01”,那么这里就有X=1,Y=2,Z=0.01三个参数
因此,如果把密度函数画在坐标系里,他需要是三维空间,如下图:
 {width=400px}
{width=400px}
这个图形很像农民带的草帽,我们通常称呼这个图形为“草帽”图形。因为密度函数必须大于等于零,所以这个草帽可以认为为平底的,又因为所有射靶所有的概率最多为1,因此,这个概率的体积最大只能为1.
理解二维密度函数图像
如果我们从俯视图的视角从下看这个草帽,可以发现他的定义域D就是一个二维平面。
 {width=400px}
{width=400px}
想想一下我们用一把刀沿着X,Y 切开草帽,因为分布函数的定义为 F(x,y)=P(X⩽x,Y⩽y)=∫−∞x∫−∞yp(x,y)dxdy ,所以,我们取的西瓜就是左边下边的那一部分。
如果把二维随机变量 (X,Y) 视为平面上随机点的坐标, 那么, 分布函数 F(x,y)在点 (x,y) 处的函数值就是随机点 (X,Y) 落在直线 X=x 的左侧和直线 Y=y 的下方以 (x,y) 为顶点的无穷直角区域内的概率, 如图所示.
例题
例 设二维连续型随机变量 (X1,X2) 与 (Y1,Y2) 的联合密度分别为 p(x,y) 和 g(x,y) ,令 f(x,y)=ap(x,y)+bg(x,y) 。要使函数 f(x,y) 是某个二维随机变量的联合密度,则 a,b 应满足
(A)a+b=1
(B)a>0,b>0
(C) 0⩽a⩽1,0⩽b⩽1
(D)a⩾0,b⩾0 ,且 a+b=1
解 f(x,y) 为密度函数 ⇔f(x,y)⩾0 且 ∫−∞+∞∫−∞+∞f(x,y)dxdy=1 ,
由此可推得, 1=a+b ,且 ap(x,y)+bg(x,y)⩾0(∀x,y∈R) .
所以选择(D).
对于 a⩾0,b⩾0 ,由 p(x,y)⩾0,g(x,y)⩾0 得
ap(x,y)+bg(x,y)⩾0(∀x,y∈R). 如果 a<0(或 b<0 ),则对一切 x,y 有
bg(x,y)⩾(−a)p(x,y) 或 ap(x,y)⩾(−b)g(x,y) 此式未必成立。
故应选(D)
例 设二维随机变量 (X,Y) 具有概率密度
f(x,y)={2e−(2x+y),0,x>0,y>0 其他 . (1) 求分布函数 F(x,y);
(2) 求概率 P(Y⩽X).
解 (1) F(x,y)=∫−∞x∫−∞yf(s,t)dsdt={∫0x∫0y2e−(2s+t)dsdt,0,x>0,y>0 其他 ,即有
F(x,y)={(1−e−2x)(1−e−y),0,x>0,y>0 其他 . (2) 将 (X,Y) 视为平面上随机点的坐标,即有 (Y⩽X)={(Y⩽X)∈G} ,其中 G 为 xOy 平面上直线 y=x 及其下方的部分,于是
P(Y⩽X)=P((Y⩽X)∈G)=∬Gf(x,y)dxdy=∫0+∞dy∫y+∞2e−(2x+y)dx=∫0+∞e−y[−e−2x]y+∞dy=∫0+∞e−3ydy=31 例 设二维随机变量 (X,Y) 的联合密度函数为
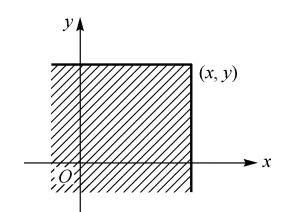
f(x,y)={cy2,0,0<x<2y, 其他. 0<y<1, 其余 求
(1)常数 c
(2) 联合分布函数 F(x,y)
(3)P(∣X∣≤Y)
解:(1)
由密度函数性质
1=∫−∞+∞∫−∞+∞f(x,y)dxdy=∫01dy∫02ycy2dx=21c 所以 c=2
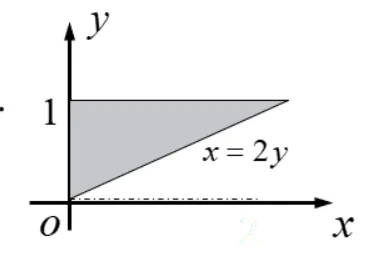
(2)由已知得
当 x<0 或 y<0 时, F(x,y)=0
当 0≤x<2y 且 0≤y<1 时, F(x,y)=∫0xdx∫2xy2y2dy=32x(y3−32x3) 当 0≤x<2 且 y≥1 时, F(x,y)=∫0xdx∫2x12y2dy=32x(1−32x3) 当 x≥2y 且 0≤y<1 时, F(x,y)=∫0ydy∫02y2y2dx=y4 当 x≥2 且 y≥ 时, F(x,y)=1 F(x,y)=⎩⎨⎧0,32x(y3−32x3),32x(1−32x3),y4,1,x<0 或 y<0;0≤x<2y,0≤y<1;0≤x<2,y≥1;x≥2y,0≤y<1;x≥2,y≥1. (3)如右图所示
P(∣X∣≤Y)=∬∣x∣≤yf(x,y)dxdy=∫01dy∫0y2y2dx=∫012y3dx=21 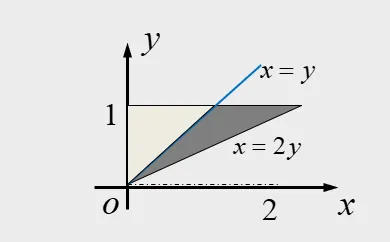
对于连续性的计算涉及大量二重积分,不熟悉的可以看本站高等数学教程。


 {width=400px}
{width=400px} {width=400px}
{width=400px}