大数定律与中心极限定理的区别 大数定律研究的是一系列随机变量 { X n } \left\{X_n\right\} { X n } X ˉ n = 1 n ∑ i = 1 n X i \bar{X}_n=\frac{1}{n} \sum_{i=1}^n X_i X ˉ n = n 1 ∑ i = 1 n X i E X ˉ n E \bar{X}_n E X ˉ n X ˉ n \bar{X}_n X ˉ n { X n } \left\{X_n\right\} { X n } X ˉ n \bar{X}_n X ˉ n
引入案列 案列1 :误差是人们经常遇到且感兴趣的随机变量, 大量的研究表明, 误差的产生是由大量微小的相互独立的随机因素叠加而成的 . 辟如一位操作者在机床上加工机械轴, 使其直径符合规定要求,但加工后的机械轴与规定要求总有一定的误差, 这是因为在加工时受到一些随机因素的影响,包括 在机床方面有机床振动与转速的影响.在刀具方面有装配与磨损的影响.在材料方面有钢材的成分、产地的影响。在操作者方面有注意力集中程度、当天的情绪的影响.在测量方面有量具误差、测量技术的影响.在环境方面有车间的温度、湿度、照明、工作电压的影响.在具体场合还可列出许多其他影响因素.
由于这些因素很多, 每个因素对加工精度的影响都是很微小的, 每个因素的出现都是随机的、是人们无法控制的、时有时无、时大时小、时正时负。这些因素的综合影响最后使每个机械轴的直径产生误差,若将这个误差记为 Y n Y_n Y n Y n Y_n Y n Y n Y_n Y n X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n Y n = X 1 + X 2 + ⋯ + X n Y_n=X_1+X_2+\cdots+X_n Y n = X 1 + X 2 + ⋯ + X n n n n n → ∞ n \rightarrow \infty n → ∞ Y n Y_n Y n Y n Y_n Y n
案例2 :导弹击中目标受到多个因素的影响包括:(1)温度 (2)湿度 (3)经纬度等影响。我们发现,虽然这些因素很多,但是这些因素每个影响都不是那么大 ,通过观察,这些“大量”“独立”“微小”的分布加起来近似呈现出“正态分布”, 在这里, 温度、湿度、风速等实际测量量很难说它们一定同分布。这不重要,只要这些“干扰因素”很小,那么他们的总和就呈现出正态分布。 这就是中心极限定理的通俗说法。
中心极限定理 (CLT) 是概率论中的真正瑰宝之一. 它的假设很弱 , 并且在实践中通常可以得到满足. 令人惊讶的是其结果的普遍性. 简而言之,对于一些相互独立的 "好" 随机变量, 伴随着变量个数的不断增加, 它们的和将收敛于正态分布 , 而正态分布的均值和方差显然由这些独立变量的均值和方差确定. 中心极限定理可以认为是现实世界的数学反映。
中心极限定理通俗的说,小误差不可避免,但是这些小的误差加起来总和呈现正态分布。
不同于大数定律,中心极限定理,不是从随机变量某个值的稳定性的角度来考虑稳定性的,而是从分布的稳定性 来考虑随机变量的稳定性。
列维一林德伯格中心极限定理(也称独立同分布中心极限定理) 设随机变量序列 X 1 , X 2 , ⋯ , X n , ⋯ X_1, X_2, \cdots, X_n, \cdots X 1 , X 2 , ⋯ , X n , ⋯ E X k = μ k E X_k=\mu_k E X k = μ k D X k = σ k 2 > 0 , k = 1 , 2 , ⋯ D X_k=\sigma_k^2>0, k=1,2, \cdots D X k = σ k 2 > 0 , k = 1 , 2 , ⋯
Y n = ∑ k = 1 n X k − E ( ∑ k = 1 n X k ) D ( ∑ k = 1 n X k ) = ∑ k = 1 n X k − n μ n σ Y_n=\dfrac{\sum_{k=1}^n X_k-E\left(\sum_{k=1}^n X_k\right)}{\sqrt{D\left(\sum_{k=1}^n X_k\right)}}=\dfrac{\sum_{k=1}^n X_k-n \mu}{\sqrt{n} \sigma} Y n = D ( ∑ k = 1 n X k ) ∑ k = 1 n X k − E ( ∑ k = 1 n X k ) = n σ ∑ k = 1 n X k − n μ 的分布函数F n ( x ) F_n(x) F n ( x ) x x x
lim n → ∞ F n ( x ) = lim n → ∞ P { ∑ k = 1 n X k − n μ n σ ⩽ x } = ∫ − ∞ x 1 2 π e − t 2 2 d t \lim _{n \rightarrow \infty} F_n(x)=\lim _{n \rightarrow \infty} P\left\{\dfrac{\sum_{k=1}^n X_k-n \mu}{\sqrt{n} \sigma} \leqslant x\right\}=\int_{-\infty}^x \dfrac{1}{\sqrt{2 \pi}} e^{-\frac{t^2}{2}} d t n → ∞ lim F n ( x ) = n → ∞ lim P { n σ ∑ k = 1 n X k − n μ ⩽ x } = ∫ − ∞ x 2 π 1 e − 2 t 2 d t 这就称随机变量序列 { X n } \left\{X_n\right\} { X n }
证明略.
从上面结论容易知道,当 n n n
Y n = ∑ k = 1 n X k − n μ n σ 2 ∼ N ( 0 , 1 ) . \boxed{
Y_n=\dfrac{\sum_{k=1}^n X_k-n \mu}{\sqrt{n \sigma^2}} \sim N(0,1) .
} Y n = n σ 2 ∑ k = 1 n X k − n μ ∼ N ( 0 , 1 ) . 或者说,当 n n n
∑ k = 1 n X k ∼ N ( n μ , n σ 2 ) \boxed{
\sum_{k=1}^n X_k \sim N\left(n \mu, n \sigma^2\right)
} k = 1 ∑ n X k ∼ N ( n μ , n σ 2 ) 虽然在一般情况下很难求出 X 1 + X 2 + ⋯ + X n X_1+X_2+\cdots+X_n X 1 + X 2 + ⋯ + X n n n n
∑ i = 1 n X i − n μ σ n ∼ 近似 N ( 0 , 1 ) ⇒ 1 n ∑ i = 1 n X i − μ σ / n ∼ 近似 N ( 0 , 1 ) ⇒ X ˉ ∼ N ( μ , σ 2 / n ) , X ˉ = 1 n ∑ i = 1 n X i . \dfrac{\sum_{i=1}^n X_i-n \mu}{\sigma \sqrt{n}} \stackrel{\text { 近似 }}{\sim} N(0,1) \Rightarrow \dfrac{\frac{1}{n} \sum_{i=1}^n X_i-\mu}{\sigma / \sqrt{n}} \stackrel{\text { 近似 }}{\sim} N(0,1) \Rightarrow \bar{X} \sim N\left(\mu, \sigma^2 / n\right), \quad \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i . σ n ∑ i = 1 n X i − n μ ∼ 近似 N ( 0 , 1 ) ⇒ σ / n n 1 ∑ i = 1 n X i − μ ∼ 近似 N ( 0 , 1 ) ⇒ X ˉ ∼ N ( μ , σ 2 / n ) , X ˉ = n 1 i = 1 ∑ n X i . 故定理又可表述为:当 n n n μ \mu μ σ 2 > 0 \sigma^2>0 σ 2 > 0 X 1 , X 2 , ⋯ , X n , ⋯ X_1, X_2, \cdots, X_n, \cdots X 1 , X 2 , ⋯ , X n , ⋯ X ˉ \bar{X} X ˉ μ \mu μ σ 2 / n \sigma^2 / n σ 2 / n
中心极限定理的通俗解释 中心极限定理通俗的解释就是:
①样本的平均值约等于总体的平均值。②不管总体是什么分布,任意一个总体的样本平均值都会围绕在总体的整体平均值周围,并且呈正态分布。
上面第一句话的意思是样本的平均值约定于或者说依概率收敛于总体的平均值。
那第二句话是什么意思呢?
比如我们进行取样,每一次取样取一百条数据,这是一个样本,样本中每条数据它的值都是服从相同分布的,我们把这一次的取样结果的平均值记为 X ‾ \overline{\mathrm{X}} X X ‾ \overline{\mathrm{X}} X X ‾ \overline{\mathrm{X}} X
这里总体的整体平均值又是什么呢?其实并不是指简单的所有数据的平均值。假设我们把V V V V V V
下面再以一个具体的例子进行说明。
假设有一个群体,如清华毕业的人,我们对这类人群的收入感兴趣。怎么知道这群人的收入呢?我们会做这样4步:
第1步.随机抽取一个样本,求该样本的平均值。例如我们抽取了100名毕业于清华的人,然后对这些人的收入求平均值。该样本里的 100名清华的人,这里的100就是该样本的大小。有一个经验是,样本大小必须达到30,中心极限定理才能保证成立。
第2步.我将第1步样本抽取的工作重复做几次,不断地从其它清华毕业的人中随机抽取 100 个人,例如我抽取了 5 个样本,并计算出每个样本的平均值,那么 5 个样本,就会有 5 个平均值。这里的 5 个样本,就是指样本数量是 5 。
第3步.根据中心极限定理,这些样本平均值中的绝大部分都极为接近总体的平均收入。有一些会稍高一点,有一些会稍低一点,只有极少数的样本平均值大大高于或低于群体平均值。
第4步.中心极限定理告诉我们,不论所研究的群体是怎样分布的,这些样本平均值会在总体平均值周围呈现一个正态分布。
为了跟上面的举例做一个衔接 。我们可以把 X 1 , X 2 , … X n \mathrm{X}_1, \mathrm{X}_2, \ldots \mathrm{X}_{\mathrm{n}} X 1 , X 2 , … X n X X X X ‾ \overline{{X}} X 1 n ∑ k = 1 n X k \frac{1}{{n}} \sum_{{k}=1}^{{n}} {X}_{{k}} n 1 ∑ k = 1 n X k μ \mu μ 1 n σ \frac{1}{\sqrt{{n}}} \sigma n 1 σ
上面的随机变量 Y Y Y Y ′ = X ˉ Y^{\prime}=\bar{X} Y ′ = X ˉ n n n X ‾ \overline{\mathrm{X}} X n n n X ˉ \bar{X} X ˉ
例一生产线生产的产品成箱包装,每箱的质量是随机的.假设每箱平均质量为 50 k g 50 kg 50 k g 5 k g 5kg 5 k g 5 t 5t 5 t 0.977 0.977 0.977
分析:我们口算一下,使用小学除法,汽车一次运送5000kg, 每箱是50 k g 50kg 50 k g 5000 ÷ 50 = 100 5000 \div 50 =100 5000 ÷ 50 = 100 ± 5 k g \pm5 kg ± 5 k g 5000 ÷ 55 = 90 5000 \div 55=90 5000 ÷ 55 = 90 5000 ÷ 45 = 111 5000 \div 45 =111 5000 ÷ 45 = 111
解:设每辆车可以装 n n n X i X_i X i i i i i = 1 , 2 , ⋯ , n i=1,2, \cdots, n i = 1 , 2 , ⋯ , n X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n E X i = 50 E X_i=50 E X i = 50 D X i = 25 D X_i=25 D X i = 25
而 n n n T n = X 1 + X 2 + ⋯ + X n T_n=X_1+X_2+\cdots+X_n T n = X 1 + X 2 + ⋯ + X n E T n = 50 n , D T n = 25 n E T_n=50 n, D T_n=25 n E T n = 50 n , D T n = 25 n T T T N ( 50 n , 25 n ) N(50 n, 25 n) N ( 50 n , 25 n )
P { T n ⩽ 5000 } = P { T n − 50 n 5 n ⩽ 5000 − 50 n 5 n } = Φ ( 1000 − 10 n n ) > 0.977 ≈ Φ ( 2 ) . \begin{gathered}
P\left\{T_n \leqslant 5000\right\}=P\left\{\frac{T_n-50 n}{5 \sqrt{n}} \leqslant \frac{5000-50 n}{5 \sqrt{n}}\right\}=\Phi\left(\frac{1000-10 n}{\sqrt{n}}\right)>0.977 \approx \Phi(2) . \\
\end{gathered} P { T n ⩽ 5000 } = P { 5 n T n − 50 n ⩽ 5 n 5000 − 50 n } = Φ ( n 1000 − 10 n ) > 0.977 ≈ Φ ( 2 ) . 由此可见,1000 − 10 n n > 2 \frac{1000-10 n}{\sqrt{n}}>2 n 1000 − 10 n > 2 n < 98.0199 n<98.0199 n < 98.0199
例题 例 设随机变量 X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n S n = X 1 + X 2 + ⋯ + X n S_n=X_1+X_2+\cdots+X_n S n = X 1 + X 2 + ⋯ + X n n n n S n S_n S n X 1 , X 2 , ⋯ , X n X_1, X_2, \cdots, X_n X 1 , X 2 , ⋯ , X n { X n } \left\{X_n\right\} { X n }
要判定当 n n n S n = ∑ i = 1 n X i S_n=\sum_{i=1}^n X_i S n = ∑ i = 1 n X i { X n } \left\{X_n\right\} { X n }
解 根据题意知,选项(A),(B)不能保证 X 1 , ⋯ , X n , ⋯ X_1, \cdots, X_n, \cdots X 1 , ⋯ , X n , ⋯
因此应选(C).
由于中心极限定理的证明需要注意:
(1)定理的三个条件"独立,同分布,期望和方差存在",缺一不可.
(2)只要 X n X_n X n n n n ∑ i = 1 n X i \sum_{i=1}^n X_i ∑ i = 1 n X i N ( n μ , n σ 2 ) N\left(n \mu, n \sigma^2\right) N ( n μ , n σ 2 ) n n n
P { a < ∑ i = 1 n X i < b } ≈ Φ ( b − n μ n σ ) − Φ ( a − n μ n σ ) P\left\{a<\sum_{i=1}^n X_i<b\right\} \approx \Phi\left(\frac{b-n \mu}{\sqrt{n} \sigma}\right)-\Phi\left(\frac{a-n \mu}{\sqrt{n} \sigma}\right) P { a < i = 1 ∑ n X i < b } ≈ Φ ( n σ b − n μ ) − Φ ( n σ a − n μ ) 这常常是解题的依据。只要题目涉及独立同分布随机变量的和 ∑ i = 1 n X i \sum_{i=1}^n X_i ∑ i = 1 n X i
例 某汽车销售点每天出售的汽车数 X X X λ = 2 \lambda=2 λ = 2 X ∼ X \sim X ∼ P ( 2 ) P(2) P ( 2 )
解 记 X i X_i X i i i i Y = X 1 + X 2 + ⋯ + X 365 Y=X_1+X_2+\cdots+X_{365} Y = X 1 + X 2 + ⋯ + X 365 E ( X i ) = D ( X i ) = 2 E\left(X_i\right)=D\left(X_i\right)=2 E ( X i ) = D ( X i ) = 2 E ( Y ) = D ( Y ) = 365 × 2 = 730 E(Y)=D(Y)=365 \times 2=730 E ( Y ) = D ( Y ) = 365 × 2 = 730
P ( Y > 700 ) = 1 − P ( Y ⩽ 700 ) = 1 − Φ ( 700 − 730 730 ) = 1 − Φ ( − 1.11 ) = 0.8665 , P(Y>700)=1-P(Y \leqslant 700)=1-\Phi\left(\frac{700-730}{\sqrt{730}}\right)=1-\Phi(-1.11)=0.8665 \text {, } P ( Y > 700 ) = 1 − P ( Y ⩽ 700 ) = 1 − Φ ( 730 700 − 730 ) = 1 − Φ ( − 1.11 ) = 0.8665 , 即该销售点一年售出 700 辆以上汽车的概率近似为 0.8665 .
高尔顿钉板实验 例 如图,有一排有一个板上面有 排钉子,每排相邻的两 个钉子之间的距离均相等。上一排钉子的水平位置恰巧位 于下一排紧邻的两个钉子水平位置的正中间。从上端入口 处放入小球,在下落过程中小球碰到钉子后以相等的可能 性向左或向右偏离,碰到下一排相邻的两个钉子中的一个。 如此继续下去,直到落入底部隔板中的一格中。问当有大 量的小球从上端依次放入,任其自由下落,问小球最终在底 板中堆积的形态. 设钉子有 16 排
X X X
X i = { − 1 , 小球碰到第 i 排钉子向左下落, 1 小球碰到第 i 排钉子向右下落。 i = 1 , ⋯ , n X_i=\left\{\begin{array}{cl}
-1, & \text { 小球碰到第 } i \text { 排钉子向左下落, } \\
1 & \text { 小球碰到第 } i \text { 排钉子向右下落。 }
\end{array} i=1, \cdots, n\right. X i = { − 1 , 1 小球碰到第 i 排钉子向左下落, 小球碰到第 i 排钉子向右下落。 i = 1 , ⋯ , n 显然 X = ∑ i = 1 n X i X=\sum_{i=1}^n X_i X = ∑ i = 1 n X i X X X X X X X i = { − 1 , 小球碰到第 i 排钉子向左下落, 1 小球碰到第 i 排钉子向右下落。 X_i=\left\{\begin{array}{cl}-1, & \text { 小球碰到第 } i \text { 排钉子向左下落,} \\ 1 & \text { 小球碰到第 } i \text { 排钉子向右下落。 }\end{array}\right. X i = { − 1 , 1 小球碰到第 i 排钉子向左下落, 小球碰到第 i 排钉子向右下落。 i = 1 , 2 , ⋯ , 16 i=1,2, \cdots, 16 i = 1 , 2 , ⋯ , 16 X 1 , ⋯ , X 16 X_1, \cdots, X_{16} X 1 , ⋯ , X 16 X = ∑ i = 1 16 X ρ X i X=\sum_{i=1}^{16} X_\rho \quad X_i X = ∑ i = 1 16 X ρ X i
E ( X i ) = − 1 × 0.5 + 1 × 0.5 = 0 , E ( X i 2 ) = ( − 1 ) 2 × 0.5 + 1 2 × 0.5 = 1 , D ( X i ) = 1 , i = 1 , ⋯ , 16 , E ( ∑ i = 1 16 X i ) = 16 × 0 = 0 , D ( ∑ i = 1 16 X i ) = 16 × 1 = 16 , \begin{aligned}
& E\left(X_i\right)=-1 \times 0.5+1 \times 0.5=0, \\
& E\left(X_i^2\right)=(-1)^2 \times 0.5+1^2 \times 0.5=1, \\
& D\left(X_i\right)=1, i=1, \cdots, 16, \\
& E\left(\sum_{i=1}^{16} X_i\right)=16 \times 0=0, D\left(\sum_{i=1}^{16} X_i\right)=16 \times 1=16,
\end{aligned} E ( X i ) = − 1 × 0.5 + 1 × 0.5 = 0 , E ( X i 2 ) = ( − 1 ) 2 × 0.5 + 1 2 × 0.5 = 1 , D ( X i ) = 1 , i = 1 , ⋯ , 16 , E ( i = 1 ∑ 16 X i ) = 16 × 0 = 0 , D ( i = 1 ∑ 16 X i ) = 16 × 1 = 16 , 由列维-林德伯格中心极限定理知 X = ∑ i = 1 16 X i ∼ 近似 N ( 0 , 16 ) X=\sum_{i=1}^{16} X_i \stackrel{\text { 近似 }}{\sim} N(0,16) X = ∑ i = 1 16 X i ∼ 近似 N ( 0 , 16 )
P ( ∣ X ∣ > 8 ) = P ( X > 8 ) + P ( X < − 8 ) ≈ 1 − Φ ( 8 − 0 16 ) + Φ ( − 8 − 0 16 ) = 2 [ 1 − Φ ( 2 ) ] = 0.0456 \begin{aligned}
P(|X|>8) & =P(X>8)+P(X<-8) \\
& \approx 1-\Phi\left(\frac{8-0}{\sqrt{16}}\right)+\Phi\left(\frac{-8-0}{\sqrt{16}}\right)=2[1-\Phi(2)]=0.0456
\end{aligned} P ( ∣ X ∣ > 8 ) = P ( X > 8 ) + P ( X < − 8 ) ≈ 1 − Φ ( 16 8 − 0 ) + Φ ( 16 − 8 − 0 ) = 2 [ 1 − Φ ( 2 )] = 0.0456 说明顾客中奖的可能性微平其微。
保险模型 例 在一家保险公司里有 10000 人参加保险,每人每年付 12 元保险费.在一年内一个人死亡的概率为 0.006 ,死亡后家属可向保险公司领取 1000 元.
试求:(1)保险公司亏本的概率;
(2)保险公司一年的利润不少于 60000 元的概率.
解(1)设参加保险的 10000 人中一年死亡的人数为 X X X X ∼ B ( 10000 , 0.006 ) , E X = X \sim B(10000,0.006), E X= X ∼ B ( 10000 , 0.006 ) , EX = 60 , D X ≈ 7.72 2 60, D X \approx 7.72^2 60 , D X ≈ 7.7 2 2
公司一年收保险费 120000 元,付给死者家属 1000 X 1000 X 1000 X 1000 X − 120000 > 0 1000 X-120000>0 1000 X − 120000 > 0 X > X> X >
P { X > 120 } = 1 − P { X ⩽ 120 } . P\{X>120\}=1-P\{X \leqslant 120\} . P { X > 120 } = 1 − P { X ⩽ 120 } . 由中心极限定理,X X X N ( 60 , 7.72 2 ) N\left(60,7.72^2\right) N ( 60 , 7.7 2 2 )
P { X > 120 } = 1 − P { X − 60 7.72 ⩽ 120 − 60 7.72 } = 1 − P { X − 60 7.72 ⩽ 7.77 } ≈ 1 − Φ ( 7.77 ) ≈ 1 − 1 = 0. \begin{aligned}
P\{X>120\} & =1-P\left\{\frac{X-60}{7.72} \leqslant \frac{120-60}{7.72}\right\}=1-P\left\{\frac{X-60}{7.72} \leqslant 7.77\right\} \\
& \approx 1-\Phi(7.77) \approx 1-1=0 .
\end{aligned} P { X > 120 } = 1 − P { 7.72 X − 60 ⩽ 7.72 120 − 60 } = 1 − P { 7.72 X − 60 ⩽ 7.77 } ≈ 1 − Φ ( 7.77 ) ≈ 1 − 1 = 0. (2)公司年利润不少于 60000 元就是 120000 − 1000 X ⩾ 60000 120000-1000 X \geqslant 60000 120000 − 1000 X ⩾ 60000 0 ⩽ X ⩽ 60 0 \leqslant X \leqslant 60 0 ⩽ X ⩽ 60
P { 0 ⩽ X ⩽ 60 } = P { 0 − 60 7.72 ⩽ X − 60 7.72 ⩽ 60 − 60 7.72 } = P { − 7.77 ⩽ X − 60 7.72 ⩽ 0 } ≈ Φ ( 0 ) − Φ ( − 7.77 ) ≈ 0.5 − 0 = 0.5. \begin{aligned}
P\{0 \leqslant X \leqslant 60\} & =P\left\{\frac{0-60}{7.72} \leqslant \frac{X-60}{7.72} \leqslant \frac{60-60}{7.72}\right\}=P\left\{-7.77 \leqslant \frac{X-60}{7.72} \leqslant 0\right\} \\
& \approx \Phi(0)-\Phi(-7.77) \approx 0.5-0=0.5 .
\end{aligned} P { 0 ⩽ X ⩽ 60 } = P { 7.72 0 − 60 ⩽ 7.72 X − 60 ⩽ 7.72 60 − 60 } = P { − 7.77 ⩽ 7.72 X − 60 ⩽ 0 } ≈ Φ ( 0 ) − Φ ( − 7.77 ) ≈ 0.5 − 0 = 0.5. 三大中心极限定理区别与应用 独立同分布的中心极限定理
lim n → ∞ P ( ∑ i = 1 n X i − n μ n σ ) ≤ x ) = ∫ − ∞ x 1 2 π e − t 2 2 d t = Φ ( x ) \left.\lim _{n \rightarrow \infty} P\left(\dfrac{\sum_{i=1}^n X_i-n \mu}{\sqrt{n} \sigma }\right) \le x \right)=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} d t=\Phi(x) lim n → ∞ P ( n σ ∑ i = 1 n X i − n μ ) ≤ x ) = ∫ − ∞ x 2 π 1 e − 2 t 2 d t = Φ ( x )
棣莫弗-拉普拉斯定理
lim n → ∞ P { X − n p n p ( 1 − p ) ⩽ x } = ∫ − ∞ x 1 2 π e − t 2 2 d t = Φ ( x ) \lim _{n \rightarrow \infty} P \left\{\dfrac{X-n p}{\sqrt{n p(1-p)}} \leqslant x\right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} dt =\Phi(x) lim n → ∞ P { n p ( 1 − p ) X − n p ⩽ x } = ∫ − ∞ x 2 π 1 e − 2 t 2 d t = Φ ( x )
李雅普诺夫定理
lim n → ∞ P { ∑ i = 1 n X i − ∑ i = 1 n μ i ∑ k = 1 n σ k 2 ⩽ x } = ∫ − ∞ x 1 2 π e − t 2 2 d t = Φ ( x ) \lim _{n \rightarrow \infty} P\left\{\dfrac{\sum_{i=1}^n X_i-\sum_{i=1}^n \mu_i }{\sqrt{\sum_{k=1}^n \sigma_k^2}} \leqslant x \right\}=\int_{-\infty}^x \frac{1}{\sqrt{2 \pi}} e ^{-\frac{t^2}{2}} d t=\Phi(x) lim n → ∞ P { ∑ k = 1 n σ k 2 ∑ i = 1 n X i − ∑ i = 1 n μ i ⩽ x } = ∫ − ∞ x 2 π 1 e − 2 t 2 d t = Φ ( x )
背景 首先,列维-林德伯格定理,也就是独立同分布的中心极限定理,适用于独立同分布的随机变量序列,只要期望和方差存在,标准化后的和趋近于正态分布。这个定理是中心极限定理中最经典的形式,应用广泛,比如在统计学中的大样本推断。
然后是棣莫弗-拉普拉斯定理,它其实是列维-林德伯格定理的一个特例,专门针对二项分布的情况。当试验次数n很大时,二项分布可以用正态分布来近似。这个定理在概率论早期由棣莫弗提出,后来拉普拉斯推广,所以名字是两个人的。
接下来是李雅普诺夫定理,属于独立不同分布情况下的中心极限定理。李雅普诺夫放宽了条件,允许随机变量不同分布,但需要满足李雅普诺夫条件,即存在某个δ>0,使得高阶矩的条件成立。这样,即使变量不同分布,只要满足条件,标准化后的和仍然趋近于正态分布。
核心条件与适用范围 定理 独立性 分布特征 矩条件 通俗理解 列维-林德伯格定理 独立同分布 同分布,存在期望和方差 仅需一阶、二阶矩存在 同分布数据的“平均化”效应,如多次测量取平均后趋近正态分布。 棣莫弗-拉普拉斯定理 独立同分布 二项分布(特殊同分布) 仅需一阶、二阶矩存在 二项分布中成功与失败的独立叠加,当试验次数极大时,整体结果呈现正态性。 是列维-林德伯格定理的特例 。 李雅普诺夫定理 独立不同分布 允许不同分布 需满足李雅普诺夫条件(存在 δ > 0 \delta >0 δ > 0 独立不同分布随机变量序列的标准化和依分布收敛于标准正态分布 。
应用场景对比 场景 适用定理 典型问题 同分布数据 列维-林德伯格定理 大样本均值估计(如重复实验测量误差分析) 。 二项分布近似 棣莫弗-拉普拉斯定理 抛硬币、抽样调查中成功次数的正态近似 。 异质数据融合 李雅普诺夫定理 多源传感器数据叠加、金融风险模型中不同资产波动的综合影响 。
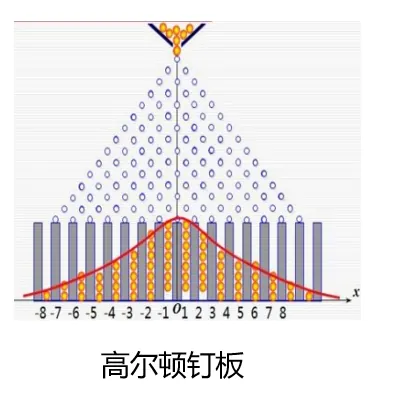 首先进行分析。小球堆积的形态取决于小球最终下落在底部隔板的位置的分布。设随机变 量 为 "小球最终下落在底部隔板中的位置" 。又引入随机变量
首先进行分析。小球堆积的形态取决于小球最终下落在底部隔板的位置的分布。设随机变 量 为 "小球最终下落在底部隔板中的位置" 。又引入随机变量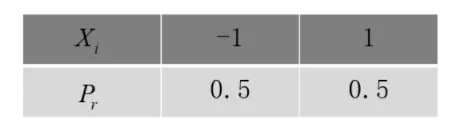 所以, 有
所以, 有